

2021年浙江省金华市婺城区中考数学模拟试卷 解析版
展开1.(3分)(﹣21)÷7的结果是( )
A.3B.﹣3C.D.
2.(3分)计算(﹣x)2•x3所得的结果是( )
A.x5B.﹣x5C.x6D.﹣x6
3.(3分)不等式组的解在数轴上表示为( )
A.B.
C.D.
4.(3分)单项式9xmy3与单项式4x2yn是同类项,则m+n的值是( )
A.2B.3C.4D.5
5.(3分)如图,点A为反比例函数图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为( )
A.﹣4B.4C.﹣2D.2
6.(3分)如图,已知正方形的边长为1,若圆与正方形的四条边都相切,则阴影部分的面积与下列各数最接近的是( )
A.0.1B.0.2C.0.3D.0.4
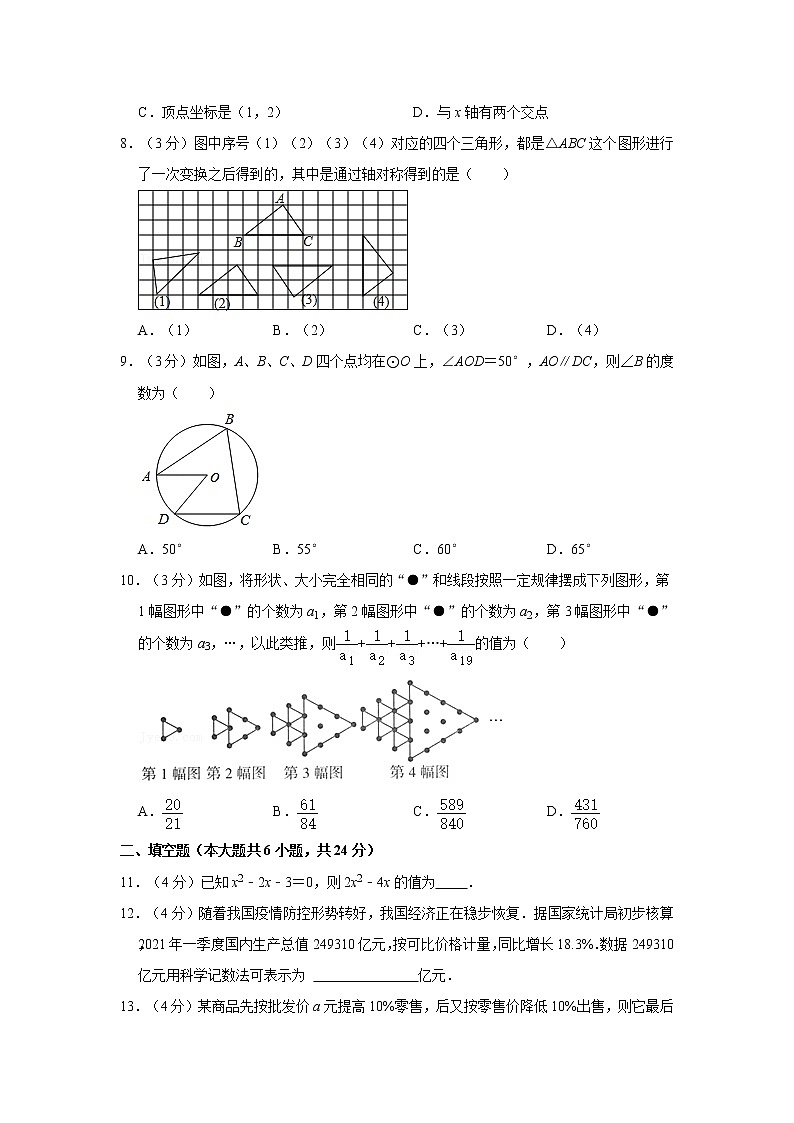
7.(3分)对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是( )
A.开口向下B.对称轴是直线x=﹣1
C.顶点坐标是(1,2)D.与x轴有两个交点
8.(3分)图中序号(1)(2)(3)(4)对应的四个三角形,都是△ABC这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是( )
A.(1)B.(2)C.(3)D.(4)
9.(3分)如图,A、B、C、D四个点均在⊙O上,∠AOD=50°,AO∥DC,则∠B的度数为( )
A.50°B.55°C.60°D.65°
10.(3分)如图,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为a1,第2幅图形中“●”的个数为a2,第3幅图形中“●”的个数为a3,…,以此类推,则+++…+的值为( )
A.B.C.D.
二、填空题(本大题共6小题,共24分)
11.(4分)已知x2﹣2x﹣3=0,则2x2﹣4x的值为 .
12.(4分)随着我国疫情防控形势转好,我国经济正在稳步恢复.据国家统计局初步核算,2021年一季度国内生产总值249310亿元,按可比价格计量,同比增长18.3%.数据249310亿元用科学记数法可表示为 亿元.
13.(4分)某商品先按批发价a元提高10%零售,后又按零售价降低10%出售,则它最后的单价是 元.
14.(4分)如果函数y=(a﹣1)x2+3x+的图象经过平面直角坐标系的四个象限,那么a的取值范围是 .
15.(4分)如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为 .
16.(4分)如图1是护眼台灯,该台灯的活动示意图如图2所示.灯柱BC=6cm,灯臂AC绕着支点C可以旋转,灯跟呈圆弧形(即弧AD和弧EF).在转动过程中,AD(EF)总是与桌面BH平行.当AC垂直BH时,AB=51cm,DM⊥MH,测得DM=42cm(点M在墙壁MH上,且MH⊥BH);当灯臂AC转到CE位置时,FN⊥MIH,测得FN=15cm,则点E到桌面的距离为 cm.若此时点C,F,M在同一条直线上,弧EF的最低点到桌面BH的距离为31cm,则弧EF所在圆的半径为 cm(保留一位小数).
三、解答题(本大题共8小题,共66分)
17.(6分)计算:|﹣3|+(﹣2021)0﹣4sin30°+()﹣1.
18.(6分)解分式方程:.
19.(6分)如图,在5×5的方格纸中,每个小正方形的边长均为1,点A,B均在小正方形的顶点上.请在图中画出满足如下条件的图形.
(1)在图1中画出一个菱形ABCD,点C、D在小正方形的顶点上;
(2)在图2中画出一个平行四边形ABCD,点C、D在小正方形的顶点上,且它的面积等于4.
20.(8分)为了把巴城建成省级文明城市,特在每个红绿灯处设置了文明监督岗,文明劝导员老张某天在市中心的一十字路口,对闯红灯的人数进行统计.根据上午7:00~12:00中各时间段(以1小时为一个时间段),对闯红灯的人数制作了如图所示的扇形统计图和条形统计图,但均不完整.请你根据统计图解答下列问题:
(1)问这一天上午7:00~12:00这一时间段共有多少人闯红灯?
(2)请你把条形统计图补充完整,并求出扇形统计图中9~10点,10~11点所对应的圆心角的度数.
(3)求这一天上午7:00~12:00这一时间段中,各时间段闯红灯的人数的众数和中位数.
21.(8分)如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC.
(1)求证:BC平分∠PBD;
(2)求证:BC2=AB•BD;
(3)若PA=6,PC=6,求BD的长.
22.(10分)为加快推进“人工智能实验区”的工作,信息中心计划购进一批机器人套件和3D打印机.经过市场考察得知,购买1份机器人套件和2台3D打印机需要3.5万元,购买2份机器人套件和1台3D打印机需要2.5万元.
(1)求每份机器人套件、每台3D打印机各多少万元?
(2)根据区内学校实际,需购进机器人套件和3D打印机共300台,总费用不超过300万元,但不低于280万元,请你通过计算求出费用最低的购买方案.
23.(10分)已知关于x的二次函数y=x2﹣2mx+m2+m的图象与关于x的函数y=kx+1的图象交于点A(x1,y1),B(x2,y2)(x1<x2).
(1)当k=0,m=0时,判断△AOB的类型;
(2)当k=1,m=0时,求AB的长;
(3)当k=1,m为任何值时,猜想AB的长是否不变?并证明你的猜想.
注:①平面内两点间的距离公式AB=;
②方程ax2+bx+c=0的两根x1,x2满足x1+x2=﹣,x1•x2=.
24.(12分)如图,在平面直角坐标系中,直线y=x+4与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c(a≠0)经过A、C两点,与x轴的另一交点为点B.
(1)求A、C两点的坐标;
(2)当△ABC为轴对称图形时,求抛物线的解析式;
(3)当△ABC关于y轴成轴对称时,若点M、N是抛物线上的动点,且有MN∥x轴,点P是x轴上的动点,在坐标平面内是否存在一点Q,使以M、N、P、Q为顶点的四边形构成正方形?若存在,求出Q点坐标;若不存在,请说明理由.
2021年浙江省金华市婺城区中考数学模拟试卷
参考答案与试题解析
一、选择题(本大题有10小题,每小题3分,共30分.请选出各题中一个符合题意的正确选项.不选、多选、错选均不给分)
1.(3分)(﹣21)÷7的结果是( )
A.3B.﹣3C.D.
【分析】根据有理数的除法法则计算即可.
【解答】解:原式=﹣3,
故选:B.
2.(3分)计算(﹣x)2•x3所得的结果是( )
A.x5B.﹣x5C.x6D.﹣x6
【分析】积的乘方,等于把每个因式分别乘方,再把所得的幂相乘;同底数幂相乘,底数不变指数相加,计算后直接选取答案.
【解答】解:(﹣x)2x3=x2•x3=x5.
故选:A.
3.(3分)不等式组的解在数轴上表示为( )
A.B.
C.D.
【分析】先解每一个不等式,再根据结果判断数轴表示的正确方法.
【解答】解:由不等式①,得2x>2,解得x>1,
由不等式②,得﹣2x≤﹣4,解得x≥2,
∴数轴表示的正确的是C选项,
故选:C.
4.(3分)单项式9xmy3与单项式4x2yn是同类项,则m+n的值是( )
A.2B.3C.4D.5
【分析】根据同类项的定义,可得m,n的值,根据有理数的加法,可得答案.
【解答】解:由题意,得
m=2,n=3.
m+n=2+3=5,
故选:D.
5.(3分)如图,点A为反比例函数图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为( )
A.﹣4B.4C.﹣2D.2
【分析】根据反比例函数系数k的几何意义:在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持不变,可计算出答案.
【解答】解:△ABO的面积为:×|﹣4|=2,
故选:D.
6.(3分)如图,已知正方形的边长为1,若圆与正方形的四条边都相切,则阴影部分的面积与下列各数最接近的是( )
A.0.1B.0.2C.0.3D.0.4
【分析】先估算出圆的面积,再根据S阴影=S正方形﹣S圆解答.
【解答】解:∵正方形的边长为1,圆与正方形的四条边都相切,
∴S阴影=S正方形﹣S圆=1﹣0.25π≈0.215.
故选:B.
7.(3分)对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是( )
A.开口向下B.对称轴是直线x=﹣1
C.顶点坐标是(1,2)D.与x轴有两个交点
【分析】根据抛物线的性质由a=1得到图象开口向上,根据顶点式得到顶点坐标为(1,2),对称轴为直线x=1,从而可判断抛物线与x轴没有公共点.
【解答】解:二次函数y=(x﹣1)2+2的图象开口向上,顶点坐标为(1,2),对称轴为直线x=1,抛物线与x轴没有公共点.
故选:C.
8.(3分)图中序号(1)(2)(3)(4)对应的四个三角形,都是△ABC这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是( )
A.(1)B.(2)C.(3)D.(4)
【分析】轴对称是沿着某条直线翻转得到新图形,据此判断出通过轴对称得到的是哪个图形即可.
【解答】解:∵轴对称是沿着某条直线翻转得到新图形,
∴通过轴对称得到的是(1).
故选:A.
9.(3分)如图,A、B、C、D四个点均在⊙O上,∠AOD=50°,AO∥DC,则∠B的度数为( )
A.50°B.55°C.60°D.65°
【分析】首先连接AD,由A、B、C、D四个点均在⊙O上,∠AOD=70°,AO∥DC,可求得∠ADO与∠ODC的度数,然后由圆的内接四边新的性质,求得答案.
【解答】解:连接AD,
∵OA=OD,∠AOD=50°,
∴∠ADO==65°.
∵AO∥DC,
∴∠ODC=∠AOC=50°,
∴∠ADC=∠ADO+∠ODC=115°,
∴∠B=180°﹣∠ADC=65°.
故选:D.
10.(3分)如图,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为a1,第2幅图形中“●”的个数为a2,第3幅图形中“●”的个数为a3,…,以此类推,则+++…+的值为( )
A.B.C.D.
【分析】首先根据图形中“●”的个数得出数字变化规律,进而求出即可.
【解答】解:a1=3=1×3,a2=8=2×4,a3=15=3×5,a4=24=4×6,…,an=n(n+2);
∴+++…+=++++…+=(1﹣+﹣+﹣+﹣+…+﹣)=(1+﹣﹣)=,
故选:C.
二、填空题(本大题共6小题,共24分)
11.(4分)已知x2﹣2x﹣3=0,则2x2﹣4x的值为 6 .
【分析】利用提取公因式法得出2x2﹣4x=2(x2﹣2x)即可得出代数式的值.
【解答】解:∵x2﹣2x﹣3=0,
∴x2﹣2x=3,
∴2x2﹣4x=2(x2﹣2x)=2×3=6.
故答案为:6.
12.(4分)随着我国疫情防控形势转好,我国经济正在稳步恢复.据国家统计局初步核算,2021年一季度国内生产总值249310亿元,按可比价格计量,同比增长18.3%.数据249310亿元用科学记数法可表示为 2.4931×105 亿元.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.
【解答】解:249310=2.4931×105,
故答案为:2.4931×105.
13.(4分)某商品先按批发价a元提高10%零售,后又按零售价降低10%出售,则它最后的单价是 0.99a 元.
【分析】原价提高10%后商品新单价为a(1+10%)元,再按新价降低10%后单价为a(1+10%)(1﹣10%),由此解决问题即可.
【解答】解:由题意得a(1+10%)(1﹣10%)=0.99a(元).
故答案为:0.99a.
14.(4分)如果函数y=(a﹣1)x2+3x+的图象经过平面直角坐标系的四个象限,那么a的取值范围是 a<﹣5 .
【分析】函数图象经过四个象限,需满足3个条件:
(Ⅰ)函数是二次函数;
(Ⅱ)二次函数与x轴有两个交点;
(Ⅲ)两个交点必须要在y轴的两侧,即两个交点异号.
【解答】解:函数图象经过四个象限,需满足3个条件:
(Ⅰ)函数是二次函数.因此a﹣1≠0,即a≠1①
(Ⅱ)二次函数与x轴有两个交点.因此△=9﹣4(a﹣1)=﹣4a﹣11>0,解得a<﹣②
(Ⅲ)两个交点必须要在y轴的两侧.因此<0,解得a<﹣5③
综合①②③式,可得:a<﹣5.
故答案为:a<﹣5.
15.(4分)如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为 10.5 .
【分析】由点E、F分别是AC、BC的中点,根据三角形中位线定理得出EF=AB=3.5为定值,则GE+FH=GH﹣EF=GH﹣3.5,所以当GH取最大值时,GE+FH有最大值.而直径是圆中最长的弦,故当GH为⊙O的直径时,GE+FH有最大值14﹣3.5=10.5.
【解答】解:当GH为⊙O的直径时,GE+FH有最大值.
当GH为直径时,E点与O点重合,
∴AC也是直径,AC=14.
∵∠ABC是直径上的圆周角,
∴∠ABC=90°,
∵∠C=30°,
∴AB=AC=7.
∵点E、F分别为AC、BC的中点,
∴EF=AB=3.5,
∴GE+FH=GH﹣EF=14﹣3.5=10.5.
故答案为:10.5.
16.(4分)如图1是护眼台灯,该台灯的活动示意图如图2所示.灯柱BC=6cm,灯臂AC绕着支点C可以旋转,灯跟呈圆弧形(即弧AD和弧EF).在转动过程中,AD(EF)总是与桌面BH平行.当AC垂直BH时,AB=51cm,DM⊥MH,测得DM=42cm(点M在墙壁MH上,且MH⊥BH);当灯臂AC转到CE位置时,FN⊥MIH,测得FN=15cm,则点E到桌面的距离为 42 cm.若此时点C,F,M在同一条直线上,弧EF的最低点到桌面BH的距离为31cm,则弧EF所在圆的半径为 71.5 cm(保留一位小数).
【分析】根据题意,通过作平行线和垂线,构造直角三角形,利用直角三角形的边角关系求出相应的边,再在圆中,利用垂径定理和勾股定理列方程求解即可.
【解答】解:延长MD,NF,则M、D、A在一条直线上,N、F、E、Q在一条直线上,
由题意得,AC=EC=AB﹣BC=51﹣6=45(cm),QE=DP=42﹣15=27(cm),
在Rt△CQE中,由勾股定理得,
QC===36(cm),
∴QB=QC+BC=36+6=42(cm),
即点E到桌面BH的距离为42cm,
过点F作FP⊥AM,垂足为P,则FP=AQ=AB﹣QB=51﹣42=9(cm),
由△MFP∽△MCA得,
=
,
即=,即=,
解得MA=75(cm),
∴EF=QN﹣QE﹣FN=75﹣27﹣15=33(cm),
如图3,可得EK=EF=cm,KL=51﹣9﹣31=11(cm),
设半径为r,则OE=r,OK=r﹣3,
在Rt△OKE中,由勾股定理得,
OE2=EK2+OK2,
即r2=()2+(r﹣11)2,
解得r=71.5(cm),
故答案为:42,71.5.
三、解答题(本大题共8小题,共66分)
17.(6分)计算:|﹣3|+(﹣2021)0﹣4sin30°+()﹣1.
【分析】直接利用绝对值的性质以及零指数幂的性质和特殊角的三角函数值、负整数指数幂的性质分别化简,再利用有理数的加减运算法则计算得出答案.
【解答】解:原式=3+1﹣4×+2
=3+1﹣2+2
=4.
18.(6分)解分式方程:.
【分析】观察两个分母可知,公分母为x﹣2,去分母,转化为整式方程求解,结果要检验.
【解答】解:去分母,得4x﹣(x﹣2)=﹣3,
去括号,得4x﹣x+2=﹣3,
移项,得4x﹣x=﹣2﹣3,
合并,得3x=﹣5,
化系数为1,得x=﹣,
检验:当x=﹣时,x﹣2≠0,
∴原方程的解为x=﹣.
19.(6分)如图,在5×5的方格纸中,每个小正方形的边长均为1,点A,B均在小正方形的顶点上.请在图中画出满足如下条件的图形.
(1)在图1中画出一个菱形ABCD,点C、D在小正方形的顶点上;
(2)在图2中画出一个平行四边形ABCD,点C、D在小正方形的顶点上,且它的面积等于4.
【分析】(1)根据菱形的判定画出图形即可.
(2)根据平行四边形的判定以及题目的条件画出图形即可.
【解答】解:(1)如图1中,菱形ABCD即为所求作.
(2)如图2中,平行四边形ABCD即为所求作.
20.(8分)为了把巴城建成省级文明城市,特在每个红绿灯处设置了文明监督岗,文明劝导员老张某天在市中心的一十字路口,对闯红灯的人数进行统计.根据上午7:00~12:00中各时间段(以1小时为一个时间段),对闯红灯的人数制作了如图所示的扇形统计图和条形统计图,但均不完整.请你根据统计图解答下列问题:
(1)问这一天上午7:00~12:00这一时间段共有多少人闯红灯?
(2)请你把条形统计图补充完整,并求出扇形统计图中9~10点,10~11点所对应的圆心角的度数.
(3)求这一天上午7:00~12:00这一时间段中,各时间段闯红灯的人数的众数和中位数.
【分析】(1)根据11﹣12点闯红灯的人数除以所占的百分比即可求出7﹣12这一时间段共有的人数;
(2)根据7﹣8点所占的百分比乘以总人数即可求出7﹣8点闯红灯的人数,同理求出8﹣9点及10﹣11点的人数,补全条形统计图即可;求出9﹣10及10﹣11点的百分比,分别乘以360度即可求出圆心角的度数;
(3)找出这一天上午7:00~12:00这一时间段中,各时间段闯红灯的人数的众数和中位数即可.
【解答】解:(1)根据题意得:40÷40%=100(人),
则这一天上午7:00~12:00这一时间段共有100人闯红灯;
(2)根据题意得:7﹣8点的人数为100×20%=20(人),
8﹣9点的人数为100×15%=15(人),
9﹣10点占=10%,
10﹣11点占1﹣(20%+15%+10%+40%)=15%,人数为100×15%=15(人),
补全图形,如图所示:
9~10点所对的圆心角为10%×360°=36°,10~11点所对应的圆心角的度数为15%×360°=54°;
(3)根据图形得:这一天上午7:00~12:00这一时间段中,各时间段闯红灯的人数的众数为15人,中位数为15人.
21.(8分)如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC.
(1)求证:BC平分∠PBD;
(2)求证:BC2=AB•BD;
(3)若PA=6,PC=6,求BD的长.
【分析】(1)连接OC,由PD为圆O的切线,利用切线的性质得到OC垂直于PD,由BD垂直于PD,得到OC与BD平行,利用两直线平行得到一对内错角相等,再由OC=OB,利用等边对等角得到一对角相等,等量代换即可得证;
(2)连接AC,由AB为圆O的直径,利用直径所对的圆周角为直角得到△ABC为直角三角形,根据一对直角相等,以及第一问的结论得到一对角相等,确定出△ABC与△BCD相似,由相似得比例,变形即可得证;
(3)由切割线定理列出关系式,将PA,PC的长代入求出PB的长,由PB﹣PA求出AB的长,确定出圆的半径,由OC与BD平行得到△PCO与△DPB相似,由相似得比例,将OC,OP,以及PB的长代入即可求出BD的长.
【解答】(1)证明:连接OC,
∵PD为圆O的切线,
∴OC⊥PD,
∵BD⊥PD,
∴OC∥BD,
∴∠OCB=∠CBD,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠CBD=∠OBC,
则BC平分∠PBD;
(2)证明:连接AC,
∵AB为圆O的直径,
∴∠ACB=90°,
∵∠ACB=∠CDB=90°,∠ABC=∠CBD,
∴△ABC∽△CBD,
∴=,即BC2=AB•BD;
(3)解:∵PC为圆O的切线,PAB为割线,
∴PC2=PA•PB,即72=6PB,
解得:PB=12,
∴AB=PB﹣PA=12﹣6=6,
∴OC=3,PO=PA+AO=9,
∵△OCP∽△BDP,
∴=,即=,
则BD=4.
22.(10分)为加快推进“人工智能实验区”的工作,信息中心计划购进一批机器人套件和3D打印机.经过市场考察得知,购买1份机器人套件和2台3D打印机需要3.5万元,购买2份机器人套件和1台3D打印机需要2.5万元.
(1)求每份机器人套件、每台3D打印机各多少万元?
(2)根据区内学校实际,需购进机器人套件和3D打印机共300台,总费用不超过300万元,但不低于280万元,请你通过计算求出费用最低的购买方案.
【分析】(1)设每份机器人套件x万元,每台3D打印机y万元,根据“购买1份机器人套件和2台3D打印机需要3.5万元,购买2份机器人套件和1台3D打印机需要2.5万元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购进机器人套件m份,则购进3D打印机(300﹣m)台,根据“总费用不超过300万元,但不低于280万元”,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,设购进机器人套件和3D打印机的总费用为w万元,利用总价=单价×数量,即可得出w关于m的函数关系式,再利用一次函数的性质,即可找出费用最低的购买方案.
【解答】解:(1)设每份机器人套件x万元,每台3D打印机y万元,
依题意得:,
解得:.
答:每份机器人套件0.5万元,每台3D打印机1.5万元.
(2)设购进机器人套件m份,则购进3D打印机(300﹣m)台,
依题意得:,
解得:150≤m≤170.
设购进机器人套件和3D打印机的总费用为w万元,则w=0.5m+1.5(300﹣m)=﹣m+450,
∵k=﹣1<0,
∴w随m的增大而减小,
∴当m=170时,w取得最小值,
∴费用最低的购买方案为:购进机器人套件170份,3D打印机130台.
23.(10分)已知关于x的二次函数y=x2﹣2mx+m2+m的图象与关于x的函数y=kx+1的图象交于点A(x1,y1),B(x2,y2)(x1<x2).
(1)当k=0,m=0时,判断△AOB的类型;
(2)当k=1,m=0时,求AB的长;
(3)当k=1,m为任何值时,猜想AB的长是否不变?并证明你的猜想.
注:①平面内两点间的距离公式AB=;
②方程ax2+bx+c=0的两根x1,x2满足x1+x2=﹣,x1•x2=.
【分析】(1)将k=0,m=0代入函数解析式,从而求得A,B两点坐标,然后结合勾股定理逆定理判断△AOB的形状;
(2)通过构造等腰直角三角形,然后结合勾股定理求解;
(3)将k=1代入函数解析式,通过联立方程组求解并结合勾股定理进行计算证明.
【解答】解:(1)△AOB是等腰直角三角形,理由如下:
当k=0时,函数y=kx+1的图象是直线y=1,
把m=0代入y=x2﹣2mx+m2+m可得,y=x2,
当x2=1时,解得x=±1,
∴A点坐标为(﹣1,1),B点坐标为(1,1),
∴OA=OB==,AB=1﹣(﹣1)=2,
∴OA2+OB2=4,AB2=4,
∴OA2+OB2=AB2,
即△AOB是等腰直角三角形;
(2)将k=1,m=0代入函数解析式,
联立方程组可得,
∴x2﹣x﹣1=0,
∴x1+x2=1,x1•x2=﹣1,
如图,设直线y=x+1与x轴交于点D,于y轴交于点G,
过点B作BE⊥x轴,过点A作AF∥x轴,AF与BE交于点C,
在直线y=x+1中,
当y=0时,x=﹣1,
当x=0时,y=1,
∴D点坐标为(﹣1,0),G点坐标为(0,1),
∴OD=OG,
∴∠BDO=45°,
又∵AF∥x轴,
∴∠BAC=45°,
∵BE⊥x轴,AF∥x轴,
∴∠BCA=90°,
∴AB=AC=(x2﹣x1)====,
即AB的长为;
(3)猜想:当k=1,m为任何值时,AB的长不变,理由如下:
当k=1时,联立方程组可得:
,
整理,可得:x2﹣(2m+1)x+m2+m﹣1=0,
∴x1+x2=2m+1,x1•x2=m2+m﹣1,
与(2)同理,AB=AC=(x2﹣x1)====.
即当k=1,m为任何值时,AB的长不变,为定值.
24.(12分)如图,在平面直角坐标系中,直线y=x+4与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c(a≠0)经过A、C两点,与x轴的另一交点为点B.
(1)求A、C两点的坐标;
(2)当△ABC为轴对称图形时,求抛物线的解析式;
(3)当△ABC关于y轴成轴对称时,若点M、N是抛物线上的动点,且有MN∥x轴,点P是x轴上的动点,在坐标平面内是否存在一点Q,使以M、N、P、Q为顶点的四边形构成正方形?若存在,求出Q点坐标;若不存在,请说明理由.
【分析】(1)将x=0,y=0分别代入一次函数解析式,从而求得一次函数与坐标轴交点坐标;
(2)分CA=CB,AB=BC,AB=AC三种情况,结合等腰三角形的性质,利用勾股定理求得B点坐标,从而利用待定系数法求二次函数解析式;
(3)分MN为正方形的边或对角线,结合正方形的性质,列方程求解.
【解答】解:(1)在y=x+4中,
当x=0时,y=4,
当y=0时,x+4=0,
解得:x=﹣3,
∴A点坐标为(﹣3,0),C点坐标为(0,4);
(2)设B点坐标为(x,0),
①当AC=BC时,
,
解得:x=﹣3(舍去)或x=3,
∴B点坐标为(3,0),
将A点坐标为(﹣3,0),B点坐标为(3,0),C点坐标为(0,4)代入y=ax2+bx+c中,
,
解得.
∴抛物线的解析式为y=﹣x2+4,
②当AB=BC时,
,
解得:x=,
∴B点坐标为(,0),
将A点坐标为(﹣3,0),B点坐标为(,0),C点坐标为(0,4)代入y=ax2+bx+c中,
,
解得,
∴抛物线的解析式为y=﹣x2﹣x+4,
③当AB=AC时,
,
解得:x=2或x=﹣8,
∴B点坐标为(2,0)或(﹣8,0),
i)将A点坐标为(﹣3,0),B点坐标为(2,0),C点坐标为(0,4)代入y=ax2+bx+c中,
,
解得,
∴抛物线的解析式为y=﹣x2﹣x+4,
ii)将A点坐标为(﹣3,0),B点坐标为(﹣8,0),C点坐标为(0,4)代入y=ax2+bx+c中,
,
解得,
∴抛物线的解析式为y=x2+x+4,
综上,当△ABC为轴对称图形时,抛物线的解析式为y=﹣x2+4或y=﹣x2﹣x+4或y=﹣x2﹣x+4或y=x2+x+4;
(3)存在,理由如下:
当△ABC关于y轴成轴对称时,则AC=BC,
此时抛物线的解析式为y=﹣x2+4,
①当MN为正方形一边时,
∵点P是x轴上的动点,且MN∥x轴,
∴此时点Q也位于x轴上,设Q点坐标为(k,0),
由正方形性质可得则P点坐标为(﹣k,0),
∴|2k|=﹣k2+4,
解得:k=±或k=±6,
∴当MN在x轴上方且为正方形的一边时,此时Q点坐标为(,0)或(﹣,0),
当MN在x轴下方且为正方形的一边时,此时Q点坐标为(6,0)或(﹣6,0),
②当MN为正方形对角线时,
∵点P是x轴上的动点,且MN∥x轴,
∴此时Q点位于y轴上,设Q点坐标为(0,k),
∴||=﹣×()2+4,
解得:k=,
∴当MN位于x轴上方且为正方形对角线时,此时Q点坐标为(0,),
当MN位于x轴下方且为正方形对角线时,此时Q点坐标为(0,),
综上,坐标平面内存在一点Q,使以M、N、P、Q为顶点的四边形构成正方形,Q点坐标为(,0)或(﹣,0),或(6,0)或(﹣6,0)或(0,)或(0,).
MP
MA
PF
AC
2023年浙江省金华市婺城区中考数学模拟试卷(一)(含解析): 这是一份2023年浙江省金华市婺城区中考数学模拟试卷(一)(含解析),共26页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2023年浙江省金华市婺城区中考数学模拟试卷(二)(含解析): 这是一份2023年浙江省金华市婺城区中考数学模拟试卷(二)(含解析),共25页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2023年浙江省金华市婺城区中考数学一模试卷(含解析): 这是一份2023年浙江省金华市婺城区中考数学一模试卷(含解析),共29页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












