2021-2022学年广东省深圳市龙岗区九年级（上）期中数学试卷

这是一份2021-2022学年广东省深圳市龙岗区九年级（上）期中数学试卷，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2021-2022学年广东省深圳市龙岗区九年级（上）期中数学试卷
一、选择题（本题有10小题，每小题3分，共30分）
1．（3分）某鱼塘里养了100条鲤鱼、若干条草鱼和50条罗非鱼，通过多次捕捞实验后发现，捕捞到草鱼的频率稳定在0.5左右，可估计该鱼塘中草鱼的数量为（　　）
A．150 B．100 C．50 D．200
2．（3分）书架上放着三本小说和两本散文，小明从中随机抽取两本，两本都是小说的概率是（　　）
A． B． C． D．
3．（3分）下列说法错误的是（　　）
A．对角线互相垂直的平行四边形是矩形
B．矩形的对角线相等
C．对角线相等的菱形是正方形
D．两组对边分别相等的四边形是平行四边形
4．（3分）如图，延长矩形ABCD的边BC至点E，使CE＝CA，连接AE，如果∠ACB＝38°，则∠E的值是（　　）

A．18° B．19° C．20° D．40°
5．（3分）如图，平行四边形ABCD中，对角线AC，BD相交于点O，点E，F分别是OA，OC的中点，下列条件中，不能判断四边形BEDF是菱形的是（　　）

A．AC⊥BD B．AC＝2BD C．AC平分∠BAD D．AB＝BC
6．（3分）矩形ABCD中，AB＝2，AD＝1，点M在边CD上，若AM平分∠DMB，则DM的长是（　　）

A． B． C． D．
7．（3分）已知a是有理数，则a2﹣2a+4的最小值是（　　）
A．3 B．5 C．6 D．8
8．（3分）用公式法解方程4y2﹣12y﹣3＝0，得到（　　）
A．y＝ B．y＝ C．y＝ D．y＝
9．（3分）方程x2﹣5x﹣6＝0左边化为两个一次因式的乘积为（　　）
A．（x﹣5x）（x﹣3）＝0 B．（x﹣2）（x+3）＝0
C．（x﹣1）（x+6）＝0 D．（x+1）（x﹣6）＝0
10．（3分）某农产品市场经销一种销售成本为40元的水产品，据市场分析，若按每千克50元销售，一个月能售出500千克：销售单价每涨1元，月销售量就减少10千克，设销售单价为每千克x元，月销售利润可以表示为（　　）
A．（x﹣40）[500﹣10（x﹣50）]元 B．（x﹣40）（10x﹣500）元
C．（x﹣40）（500﹣10x）元 D．（x﹣40）[500﹣10（50﹣x）]元
二、填空题（本题有5小题，每小题3分，共15分）
11．（3分）把方程2x2﹣x﹣6＝0配方，化为（x+m）2＝n的形式为 　 　．
12．（3分）已知x＝2是关于x的一元二次方程kx2+（k2﹣2）x+2k+4＝0的一个根，则k的值为 　 　．
13．（3分）有两双完全相同的鞋，从中任取两只，恰好成为一双的概率为 　 　．
14．（3分）某种商品原价每件40元，经两次降价，现售价每件32.4元，则该种商品平均每次降价的百分率是 　 　．
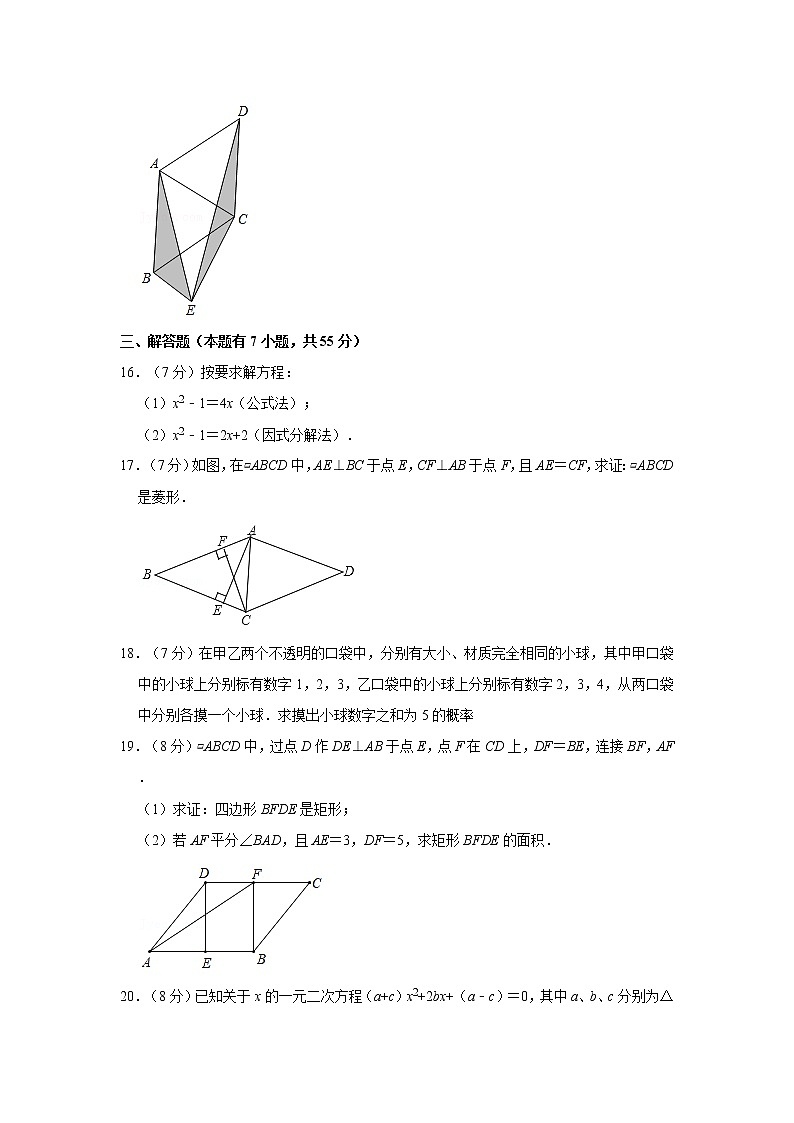
15．（3分）如图，在菱形ABCD中，AC＝6，AB＝5，点E是直线AB、CD之间任意一点，连接AE、BE、DE、CE，则△EAB和△ECD的面积和等于 　 　．

三、解答题（本题有7小题，共55分）
16．（7分）按要求解方程：
（1）x2﹣1＝4x（公式法）；
（2）x2﹣1＝2x+2（因式分解法）．
17．（7分）如图，在▱ABCD中，AE⊥BC于点E，CF⊥AB于点F，且AE＝CF，求证：▱ABCD是菱形．

18．（7分）在甲乙两个不透明的口袋中，分别有大小、材质完全相同的小球，其中甲口袋中的小球上分别标有数字1，2，3，乙口袋中的小球上分别标有数字2，3，4，从两口袋中分别各摸一个小球．求摸出小球数字之和为5的概率
19．（8分）▱ABCD中，过点D作DE⊥AB于点E，点F在CD上，DF＝BE，连接BF，AF．
（1）求证：四边形BFDE是矩形；
（2）若AF平分∠BAD，且AE＝3，DF＝5，求矩形BFDE的面积．

20．（8分）已知关于x的一元二次方程（a+c）x2+2bx+（a﹣c）＝0，其中a、b、c分别为△ABC三边的长．
（1）如果x＝﹣1是方程的根，试判断△ABC的形状，并说明理由；
（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由．
21．（8分）用长12m的一根铁丝围成长方形．
（1）如果长方形的面积为5m2，那么此时长方形的长是多少？宽是多少？
（2）能否围成面积是10m2的长方形？为什么？
22．（10分）已知：如图，菱形ABCD的对角线AC与BD相交于点O，若∠CAD＝∠DBC．
（1）求证：四边形ABCD是正方形．
（2）E是OB上一点，DH⊥CE，垂足为H，DH与OC相交于点F，求证：OE＝OF．


2021-2022学年广东省深圳市龙岗区九年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本题有10小题，每小题3分，共30分）
1．（3分）某鱼塘里养了100条鲤鱼、若干条草鱼和50条罗非鱼，通过多次捕捞实验后发现，捕捞到草鱼的频率稳定在0.5左右，可估计该鱼塘中草鱼的数量为（　　）
A．150 B．100 C．50 D．200
【分析】根据大量重复试验中的频率估计出概率，利用概率公式求得草鱼的数量即可．
【解答】解：∵通过多次捕捞实验后发现，捕捞到草鱼的频率稳定在0.5左右，
∴捕捞到草鱼的概率约为0.5，
设有草鱼x条，根据题意得：
＝0.5，
解得：x＝150，
故选：A．
2．（3分）书架上放着三本小说和两本散文，小明从中随机抽取两本，两本都是小说的概率是（　　）
A． B． C． D．
【分析】画树状图（用A、B、C表示三本小说，a、b表示两本散文）展示所有20种等可能的结果数，找出从中随机抽取2本都是小说的结果数，然后根据概率公式求解．
【解答】解：画树状图为：（用A、B、C表示三本小说，a、b表示两本散文）
共有20种等可能的结果数，其中从中随机抽取2本都是小说的结果数为6，
所以从中随机抽取2本都是小说的概率＝＝．
故选：A．

3．（3分）下列说法错误的是（　　）
A．对角线互相垂直的平行四边形是矩形
B．矩形的对角线相等
C．对角线相等的菱形是正方形
D．两组对边分别相等的四边形是平行四边形
【分析】根据各个选项中的说法，可以判断是否正确，从而可以解答本题．
【解答】解：对角线互相垂直的平行四边形是菱形，故选项A错误；
矩形的对角线相等，故选项B正确；
对角线相等的菱形是正方形，故选项C正确；
两组对边分别相等的四边形是平行四边形，故选项D正确；
故选：A．
4．（3分）如图，延长矩形ABCD的边BC至点E，使CE＝CA，连接AE，如果∠ACB＝38°，则∠E的值是（　　）

A．18° B．19° C．20° D．40°
【分析】由等腰三角形的性质可得∠E＝∠CAE，由外角的性质可求解．
【解答】解：∵CE＝CA，
∴∠E＝∠CAE，
∵∠ACB＝∠E+∠CAE＝2∠E，
∴∠E＝19°
故选：B．
5．（3分）如图，平行四边形ABCD中，对角线AC，BD相交于点O，点E，F分别是OA，OC的中点，下列条件中，不能判断四边形BEDF是菱形的是（　　）

A．AC⊥BD B．AC＝2BD C．AC平分∠BAD D．AB＝BC
【分析】由点E，F分别是OA，OC的中点得出OF＝OE，证出四边形EBFD是平行四边形，添加AC⊥BD时，得出BE＝BF，四边形BEDF是菱形，①正确；添加AC平分∠BAD，得出∠DAC＝∠BAC，证出BE＝DE，因此四边形EBDF是菱形，选项C正确；
添加AB＝AC，可证得BE＝BF，则四边形EBDF是菱形，选项D正确；只有添加选项B不能判定四边形EBFD是菱形；即可得出结论．
【解答】解：∵四边形ABCD是平行四边形，
∴OA＝OC，OB＝OD，
∵点E，F分别是OA，OC的中点，
∴OE＝OF＝＝，
∴四边形EBDF是平行四边形，
添加AC⊥BD时，
∵BO是△BEF的中线，
∴BE＝BF，
∴四边形EBFD是菱形，选项A正确；
添加AC平分∠BAD，
∴∠DAC＝∠BAC＝∠ACB，
∴AD＝AB＝BC，
在△ABE和△ADE中，，
∴△ABE≌△ADE（SAS），
∴BE＝DE，
∴四边形EBFD是菱形，选项C正确；
添加AB＝BC时，
∴∠BAE＝∠BCF，
在△BAE和△BCF中，，
∴△BAE≌△BCF（SAS），
∴BE＝BF，
∴四边形EBFD是菱形，选项D正确；
只有添加选项B不能判定四边形EBFD是菱形；
故选：B．
6．（3分）矩形ABCD中，AB＝2，AD＝1，点M在边CD上，若AM平分∠DMB，则DM的长是（　　）

A． B． C． D．
【分析】由矩形的性质得出CD＝AB＝2，AB∥CD，BC＝AD＝1，∠C＝90°，由平行线的性质得出∠BAM＝∠AMD，再由角平分线证出∠BAM＝∠AMB，得出MB＝AB＝2，由勾股定理求出CM，即可得出DM的长．
【解答】解：∵四边形ABCD是矩形，
∴CD＝AB＝2，AB∥CD，BC＝AD＝1，∠C＝90°，
∴∠BAM＝∠AMD，
∵AM平分∠DMB，
∴∠AMD＝∠AMB，
∴∠BAM＝∠AMB，
∴BM＝AB＝2，
∴CM＝＝＝，
∴DM＝CD﹣CM＝2﹣；
故选：D．
7．（3分）已知a是有理数，则a2﹣2a+4的最小值是（　　）
A．3 B．5 C．6 D．8
【分析】原式变形后，利用完全平方公式配方，并利用非负数的性质求出最小值即可．
【解答】解：a2﹣2a+4＝（a2﹣2a+1）+3＝（a﹣1）2+3，
∵（a﹣1）2≥0，
∴（a﹣1）2+3≥3，即a2﹣2a+4≥3，
则a2﹣2a+4的最小值是3，
故选：A．
8．（3分）用公式法解方程4y2﹣12y﹣3＝0，得到（　　）
A．y＝ B．y＝ C．y＝ D．y＝
【分析】先得出a、b、c的值，再计算出判别式的值，继而代入求根公式即可．
【解答】解：∵a＝4，b＝﹣12，c＝﹣3，
∴Δ＝（﹣12）2﹣4×4×（﹣3）＝192＞0，
∴y＝＝＝，
故选：C．
9．（3分）方程x2﹣5x﹣6＝0左边化为两个一次因式的乘积为（　　）
A．（x﹣5x）（x﹣3）＝0 B．（x﹣2）（x+3）＝0
C．（x﹣1）（x+6）＝0 D．（x+1）（x﹣6）＝0
【分析】将左边用十字相乘法因式分解即可．
【解答】解：∵x2﹣5x﹣6＝0，
∴（x﹣6）（x+1）＝0，
故选：D．
10．（3分）某农产品市场经销一种销售成本为40元的水产品，据市场分析，若按每千克50元销售，一个月能售出500千克：销售单价每涨1元，月销售量就减少10千克，设销售单价为每千克x元，月销售利润可以表示为（　　）
A．（x﹣40）[500﹣10（x﹣50）]元 B．（x﹣40）（10x﹣500）元
C．（x﹣40）（500﹣10x）元 D．（x﹣40）[500﹣10（50﹣x）]元
【分析】直接利用每千克利润×销量＝总利润，进而得出关系式．
【解答】解：设销售单价为每千克x元，则月销售利润＝（x﹣40）[500﹣10（x﹣50）]．
故选：A．
二、填空题（本题有5小题，每小题3分，共15分）
11．（3分）把方程2x2﹣x﹣6＝0配方，化为（x+m）2＝n的形式为 　（x﹣）2＝　．
【分析】根据配方法即可求出答案．
【解答】解：∵2x2﹣x﹣6＝0，
∴x2﹣x＝3，
∴x2﹣+＝，
∴（x﹣）2＝，
∴故答案为：（x﹣）2＝．
12．（3分）已知x＝2是关于x的一元二次方程kx2+（k2﹣2）x+2k+4＝0的一个根，则k的值为 　﹣3　．
【分析】把x＝2代入kx2+（k2﹣2）x+2k+4＝0得4k+2k2﹣4+2k+4＝0，再解关于k的方程，然后根据一元二次方程的定义确定k的值．
【解答】解：把x＝2代入kx2+（k2﹣2）x+2k+4＝0得4k+2k2﹣4+2k+4＝0，
整理得k2+3k＝0，解得k1＝0，k2＝﹣3，
因为k≠0，
所以k的值为﹣3．
故答案为﹣3．
13．（3分）有两双完全相同的鞋，从中任取两只，恰好成为一双的概率为 　　．
【分析】设其中一双鞋分别为a，a′；画出树状图，可知共有12种情况，能配成一双的有8种情况，根据概率公式计算即可；
【解答】解：设其中一双鞋分别为a，a′；
画树状图得：

∵共有12种情况，能配成一双的有8种情况，
∴取出两只刚好配一双鞋的概率是：＝．
故答案为：．
14．（3分）某种商品原价每件40元，经两次降价，现售价每件32.4元，则该种商品平均每次降价的百分率是 　10%　．
【分析】设降价百分率为x，根据售价从原来每件40元经两次降价后降至每件32.4元，可列方程求解．
【解答】解：设降价百分率为x，
列方程：40（1﹣x）2＝32.4．
解得x1＝0.1，x2＝1.9（不合题意舍去）．
故答案为：10%．
15．（3分）如图，在菱形ABCD中，AC＝6，AB＝5，点E是直线AB、CD之间任意一点，连接AE、BE、DE、CE，则△EAB和△ECD的面积和等于 　12　．

【分析】连接BD，根据菱形对角线的性质，利用勾股定理计算BD的长，根据两平行线的距离相等，所以△EAB和△ECD的面积和等于平行四边形EGHF的面积的一半，再利用菱形面积等于对角线积的一半计算可得结论．
【解答】解：连接BD交AC于O，
∵四边形ABCD是菱形，
∴AC⊥BD，OA＝AC＝×6＝3，
∵AB＝5，
由勾股定理得：OB＝4，
∴BD＝2OB＝8，
∵AB∥CD，
∴△EAB和△ECD的高的和等于点C到直线AB的距离，
∴△EAB和△ECD的面积和＝×菱形ABCD的面积＝×＝＝12．
故答案为：12

三、解答题（本题有7小题，共55分）
16．（7分）按要求解方程：
（1）x2﹣1＝4x（公式法）；
（2）x2﹣1＝2x+2（因式分解法）．
【分析】（1）方程利用公式法求出解即可；
（2）方程利用因式分解法求出解即可．
【解答】解：（1）整理得x2﹣4x﹣1＝0，
∵a＝1，b＝﹣4，c＝﹣1，
∴b2﹣4ac＝16﹣4×1×（﹣1）＝20＞0，
∴x＝＝＝2±，
∴x1＝2+，x2＝2﹣；
（2）整理得x2﹣2x﹣3＝0，
∴（x﹣3）（x+1）＝0
∴x1＝3，x2＝﹣1．
17．（7分）如图，在▱ABCD中，AE⊥BC于点E，CF⊥AB于点F，且AE＝CF，求证：▱ABCD是菱形．

【分析】根据AAS证明△ABE≌△CBF，进而利用全等三角形的性质得出BC＝BA，进而利用菱形的判定证明即可．
【解答】证明：∵AE⊥BC于点E，CF⊥AB于点F，
∴∠CFB＝∠AEB＝90°，
在△ABE与△CBF中
，
∴△ABE≌△CBF（AAS），
∴BC＝BA
∵四边形ABCD是平行四边形，
∴▱ABCD是菱形．
18．（7分）在甲乙两个不透明的口袋中，分别有大小、材质完全相同的小球，其中甲口袋中的小球上分别标有数字1，2，3，乙口袋中的小球上分别标有数字2，3，4，从两口袋中分别各摸一个小球．求摸出小球数字之和为5的概率
【分析】根据题意画出树状图得出所有等情况数和摸出小球数字之和为5的情况数，再根据概率公式即可得出答案．
【解答】解：根据题意画图如下：

由树状图可知，共有9种情况，每种情况的可能性相等．摸出的两个小球数字之和为5有3种情况，
则P（数字之和为5）＝＝．
19．（8分）▱ABCD中，过点D作DE⊥AB于点E，点F在CD上，DF＝BE，连接BF，AF．
（1）求证：四边形BFDE是矩形；
（2）若AF平分∠BAD，且AE＝3，DF＝5，求矩形BFDE的面积．

【分析】（1）根据平行四边形的性质，可得AB与CD的关系，根据平行四边形的判定，可得BFDE是平行四边形，再根据矩形的判定，可得答案；
（2）由平行线和角平分线定义得出∠DFA＝∠DAF，证出AD＝DF＝5，由勾股定理求出DE＝＝4，即可得出矩形BFDE的面积．
【解答】（1）证明：∵四边形ABCD是平行四边形，
∴AB∥CD．
∵BE∥DF，BE＝DF，
∴四边形BFDE是平行四边形．
∵DE⊥AB，
∴∠DEB＝90°，
∴四边形BFDE是矩形；
（2）解：∵AB∥CD，
∴∠BAF＝∠DFA，
∵AF平分∠BAD，
∴∠BAF＝∠DAF，
∴∠DFA＝∠DAF，
∴AD＝DF＝5，
∵DE⊥AB，
∴∠AED＝90°，
由勾股定理得：DE＝＝4，
∴矩形BFDE的面积＝DF×DE＝5×4＝20．
20．（8分）已知关于x的一元二次方程（a+c）x2+2bx+（a﹣c）＝0，其中a、b、c分别为△ABC三边的长．
（1）如果x＝﹣1是方程的根，试判断△ABC的形状，并说明理由；
（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由．
【分析】（1）根据方程解的定义把x＝﹣1代入方程得到（a+c）×（﹣1）2﹣2b+（a﹣c）＝0，整理得a﹣b＝0，即a＝b，于是根据等腰三角形的判定即可得到△ABC是等腰三角形；
（2）根据判别式的意义得到Δ＝（2b）2﹣4（a+c）（a﹣c）＝0，整理得a2＝b2+c2，然后根据勾股定理的逆定理得到△ABC是直角三角形．
【解答】解：（1）△ABC是等腰三角形．理由如下：
∵x＝﹣1是方程的根，
∴（a+c）×（﹣1）2﹣2b+（a﹣c）＝0，
∴a+c﹣2b+a﹣c＝0，
∴a﹣b＝0，
∴a＝b，
∴△ABC是等腰三角形；
（2）△ABC是直角三角形．理由如下：
∵方程有两个相等的实数根，
∴Δ＝（2b）2﹣4（a+c）（a﹣c）＝0，
∴4b2﹣4a2+4c2＝0，
∴a2＝b2+c2，
∴△ABC是直角三角形．
21．（8分）用长12m的一根铁丝围成长方形．
（1）如果长方形的面积为5m2，那么此时长方形的长是多少？宽是多少？
（2）能否围成面积是10m2的长方形？为什么？
【分析】（1）由于长方形的面积为5m2，由此列出方程x（6﹣x）＝5，解方程即可求解；
（2）由于长方形的面积为10m2，由此列出方程x（6﹣x）＝10，判断方程的根的情况即可求解．
【解答】解：（1）设长方形的宽为xm，则长为（6﹣x）m，
根据题意得x（6﹣x）＝5，
解得x1＝5，x2＝1，又x＜6﹣x，
∴x1＝5 （舍去）．
∴当长方形的宽为1m，长为（6﹣x）m＝5m时，面积为5m2．
（2）当面积为10m2时，x（6﹣x）＝10，
即x2﹣6x+10＝0，此时Δ＝36﹣40＜0，故此方程无实数根，这样的长方形不存在．
22．（10分）已知：如图，菱形ABCD的对角线AC与BD相交于点O，若∠CAD＝∠DBC．
（1）求证：四边形ABCD是正方形．
（2）E是OB上一点，DH⊥CE，垂足为H，DH与OC相交于点F，求证：OE＝OF．

【分析】（1）由菱形的性质得出AD∥BC，∠BAD＝2∠DAC，∠ABC＝2∠DBC，得出∠BAD+∠ABC＝180°，证出∠BAD＝∠ABC，求出∠BAD＝90°，即可得出结论；
（2）由正方形的性质得出AC⊥BD，AC＝BD，CO＝AC，DO＝BD，得出∠COB＝∠DOC＝90°，CO＝DO，证出∠ECO＝∠EDH，证明△ECO≌△FDO（ASA），
即可得出结论．
【解答】（1）证明：∵四边形ABCD是菱形，
∴AD∥BC，∠BAD＝2∠DAC，∠ABC＝2∠DBC，
∴∠BAD+∠ABC＝180°，
∵∠CAD＝∠DBC，
∴∠BAD＝∠ABC，
∴2∠BAD＝180°，∴∠BAD＝90°，
∴四边形ABCD是正方形；
（2）证明：∵四边形ABCD是正方形，
∴AC⊥BD，AC＝BD，CO＝AC，DO＝BD，
∴∠COB＝∠DOC＝90°，CO＝DO，
∵DH⊥CE，垂足为H，
∴∠DHE＝90°，∠EDH+∠DEH＝90°，
∵∠ECO+∠DEH＝90°，
∴∠ECO＝∠EDH，
在△ECO和△FDO中，，
∴△ECO≌△FDO（ASA），
∴OE＝OF．