初中苏科版11.1 反比例函数教案设计

这是一份初中苏科版11.1 反比例函数教案设计，共5页。教案主要包含了三象限内；等内容，欢迎下载使用。
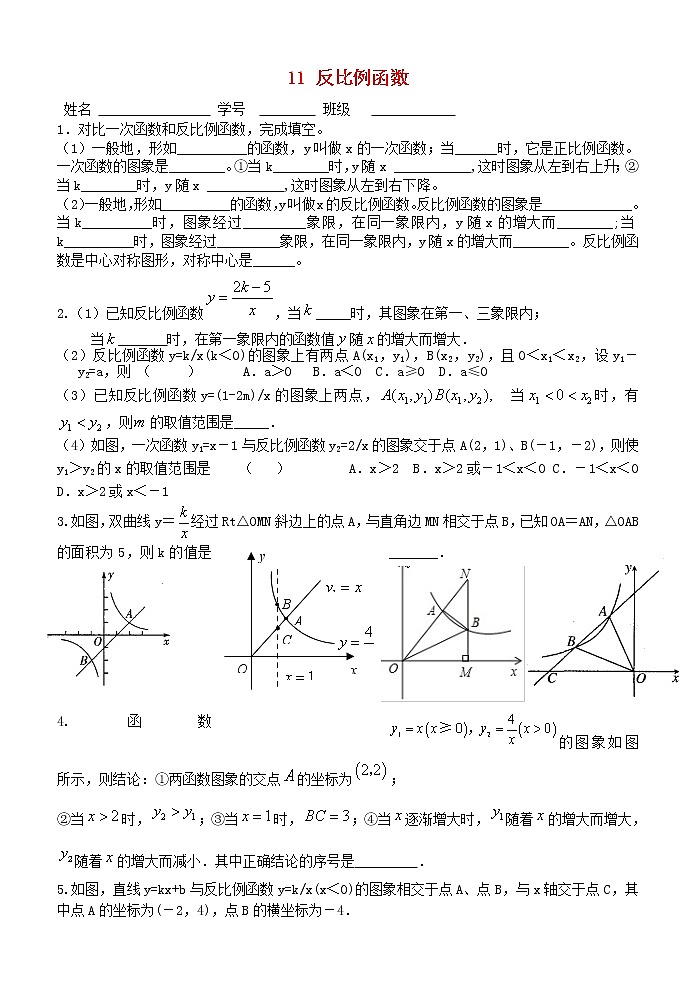
11 反比例函数 姓名                  学号           班级                    1．对比一次函数和反比例函数，完成填空。（1）一般地，形如__________的函数，y叫做x的一次函数；当______时，它是正比例函数。一次函数的图象是________。①当k________时，y随x ___________,这时图象从左到右上升；②当k________时，y随x ___________,这时图象从左到右下降。（2）一般地，形如__________的函数，y叫做x的反比例函数。反比例函数的图象是_____________。当k__________时，图象经过_________象限，在同一象限内，y随x的增大而________;当k__________时，图象经过_________象限，在同一象限内，y随x的增大而________。反比例函数是中心对称图形，对称中心是______。2.（1）已知反比例函数，当_____时，其图象在第一、三象限内；当___  __时，在第一象限内的函数值随的增大而增大．（2）反比例函数y=k/x(k＜0)的图象上有两点A(x1，y1)，B(x2，y2)，且0＜x1＜x2，设y1－y2=a，则 （     ）      A．a＞0   B．a＜0  C．a≥0  D．a≤0                      （3）已知反比例函数y=(1-2m)/x的图象上两点，  当时，有，则的取值范围是_____．（4）如图，一次函数y1=x－1与反比例函数y2=2/x的图象交于点A(2，1)、B(－1，－2)，则使y1＞y2的x的取值范围是    （   ）        A．x＞2  B．x＞2或－1＜x＜0 C．－1＜x＜0 D．x＞2或x＜－13.如图，双曲线y＝经过Rt△OMN斜边上的点A，与直角边MN相交于点B，已知OA＝AN，△OAB的面积为5，则k的值是_______． 4.函数的图象如图所示，则结论：①两函数图象的交点的坐标为；②当时，；③当时，；④当逐渐增大时，随着的增大而增大，随着的增大而减小．其中正确结论的序号是         ．5.如图，直线y=kx+b与反比例函数y=k/x(x＜0)的图象相交于点A、点B，与x轴交于点C，其中点A的坐标为(－2，4)，点B的横坐标为－4．(1)试确定反比例函数的关系式；            (2)求△AOB的面积．（3）补全双曲线，求出k/x＜kx+b时x的取值范围。  6.已知y=+，与x成正比例，与x+1成反比例，且当x=1时，y=3.5；当x=2时，y=5.求x=–2时，y的值。 7.已知函数的图象有两个交点，其中一个交点的横坐标为1，则          .如图,已知关于x的函数y=k(x-1)和y=-(k≠0), 它们在同一坐标系内的图象大致是(  )     8.如图，点A(x1，y1)、B(x2，y2)都在双曲线y＝ (x>0)上，且x2－x1＝4，y1－y2＝2；分别过点A、B向x轴、y轴作垂线段，垂足分别为C、D、E、F，AC与BF相交于G点，四边形FOCG的面积为2，五边形AEODB的面积为14，那么双曲线的解析式为_______．      9.如图，直线y=2x+2与y轴交于A点，与反比例函数y＝（x＞0）的图象交于点M，过M作MH⊥x轴于点H，且AO=2OH．
（1）求k的值；（2）点N（a，1）是反比例函数 y＝（x＞0）图象上的点，在x轴上是否存在点P，使得PM+PN最小？若存在，求出点P的坐标；若不存在，请说明理由．     10.如图，已知正比例函数y=2x和反比例函数的图象交于点A（m，-2）．
（1）求反比例函数的解析式；
（2）观察图象，直接写出正比例函数值大于反比例函数值时自变量x的取值范围；
（3）若双曲线上点C（2，n）沿OA方向平移 个单位长度得到点B，判断四边形OABC的形状并证明你的结论．    初二数学练习        班级：__________  姓名：__________1．函数y=中,当x=时,y=_____;当x=_______时,y= －1.2.已知函数y=kx的图象经过点(2,-6),则函数y=的解析式可确定为______，反比例函数在每个象限内，y随x的增大而____________。3．已知y与2x+1成反比例,且当x=1时,y=2,那么当x=0时,y=________.4．已知反比例函数y=,当x>0时,y随x的________而增大.5.点 A（，）、B(, )均在反比例函数的图象上，若 ＜0，则 _____.6．正比例函数y=k1x(k1≠0)和反比例函数y=(k2≠0)的一个交点为(m,n),则另一个交点为          7.如图，函数y＝－x与函数y＝－的图像相交于A、B两点，过A、B两点分别作y轴的垂线，垂足分别为点C、D，则四边形ACBD的面积为_______8.如图，△OAB中，C是AB的中点，反比例函数y＝（k>0）在第一象限的图象经过A、C两点，若△OAB面积为6，则k的值为            9．已知一次函数y=kx+b的图象经过第一、二、三象限,则函数y=的图象A.第一、三象限     B.第二、四象限  C.第三、四象限     D.第一、二象限      (     )10.当x>0时,两个函数值y一个随x的增大而增大另一个随x的增大而减少 的是        (      )A.y=3x与y=  B.y=3x与y=-    C.y=-2x+6与y=     D.y=3x-15与y=-11、在直角坐标系中，直线y=6-x与函数 y=4/x (x>0)的图象相交于点  A、B，设点A的坐标为(，y1  )，那么长为,宽为y1的矩形面积分别为(    )    A．2   B．4   C．8    D．1212.若点A(-2,y1),B(-1, y2),C(1, y3)在反比例函数y=（k＜0）的图象上，则下列结论正确的是(   ) A.>>   B.>>   C.>>    D.>>13.如图，双曲线经过矩形QABC的边BC的中点E，交AB于点D。若梯形ODBC的面积为3，则双曲线的解析式为A．     B．   C．      D．    (     )14．已知：两点，反比例函数与线段相交，过反比例函数上任意一点作轴的垂线为垂足，为坐标原点，则面积的取值范围是(         )Ａ．  Ｂ．  C     Ｄ．或     15.如图，反比例函数的图像与一次函数y＝kx－3的图像在第一象限内的交点坐标为A(4，m)．  (1)求m的值及一次函数的表达式，  (2)若直线x＝2与反比例函数和一次函数的图像分别交于点B、C，求线段BC的长．  16正方形OABC的面积为9，点O是坐标原点，点A在x轴上，点C在y轴上，点B在函数y＝（k>0，x>0）的图象上，点P(m、n)是函数y＝上任意一点，过点P分别作x轴、y轴的垂线，垂足分别为E、F，并设矩形OEPF中和正方形OABC不重合部分的面积为S． (1)求点B的坐标和k值；  (2)当S＝时，求P点的坐标．      17.如图，直线y=k和双曲线y＝过P点作PA0垂直x轴，垂足为A0，x轴上的点A0、A1、A2、…An的横坐标是连续的整数，过点A1、A2、…An分别作x轴的垂线，与双曲线y＝（x＞0）及直线y=k分别交于点B1、B2、…Bn，C1、C2、…Cn。（1）求A0点坐标；   （2）求的值；（3）试猜想的值。（直接写答案）   18.在平面直角坐标系中，点A（-3，4）关于y轴的对称点为点B，连接AB，反比例函数y＝（x＞0）的图象经过点B，过点B作BC⊥x轴于点C，点P是该反比例函数图象上任意一点，过点P作PD⊥x轴于点D，点Q是线段AB上任意一点，连接OQ、CQ．
（1）求k的值；
（2）判断△QOC与△POD的面积是否相等，并说明理由．