初中苏科版5.2 二次函数的图象和性质教学设计

这是一份初中苏科版5.2 二次函数的图象和性质教学设计，共2页。
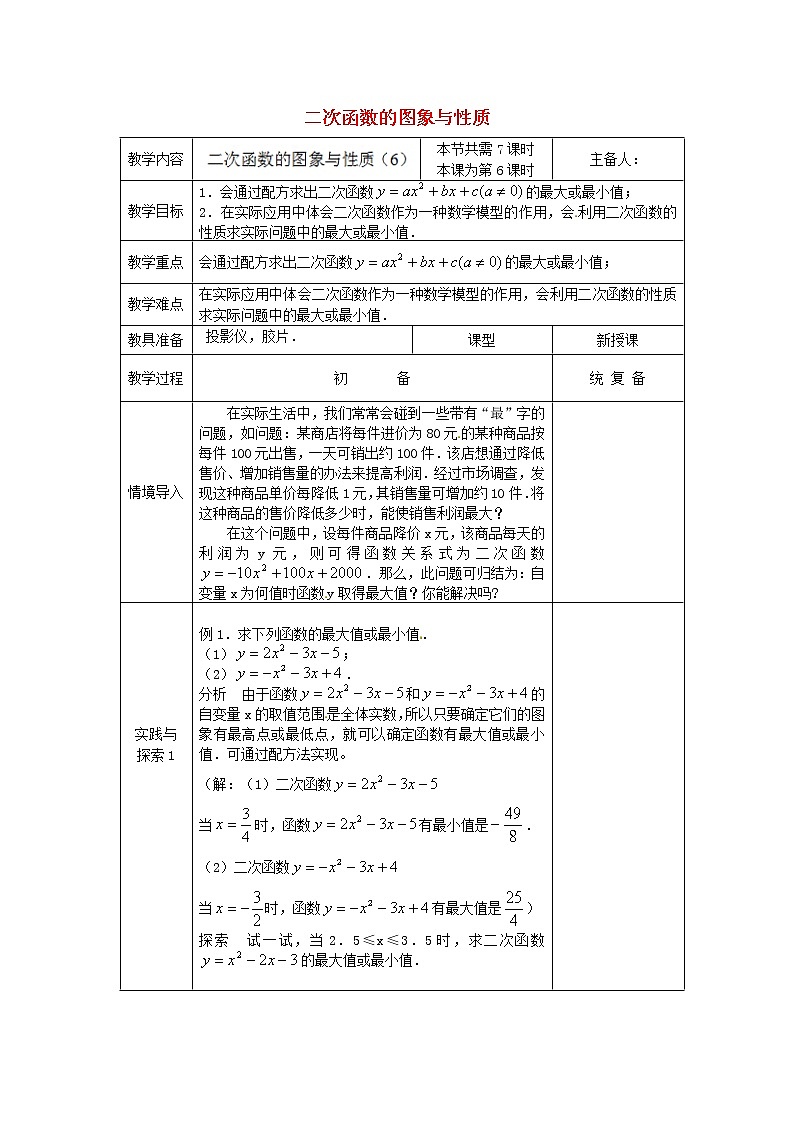
二次函数的图象与性质教学内容本节共需7课时本课为第6课时主备人： 教学目标1．会通过配方求出二次函数的最大或最小值；2．在实际应用中体会二次函数作为一种数学模型的作用，会利用二次函数的性质求实际问题中的最大或最小值．教学重点会通过配方求出二次函数的最大或最小值；教学难点在实际应用中体会二次函数作为一种数学模型的作用，会利用二次函数的性质求实际问题中的最大或最小值．教具准备 投影仪，胶片．课型新授课教学过程初       备统 复 备情境导入 在实际生活中，我们常常会碰到一些带有“最”字的问题，如问题：某商店将每件进价为80元的某种商品按每件100元出售，一天可销出约100件．该店想通过降低售价、增加销售量的办法来提高利润．经过市场调查，发现这种商品单价每降低1元，其销售量可增加约10件．将这种商品的售价降低多少时，能使销售利润最大？在这个问题中，设每件商品降价x元，该商品每天的利润为y元，则可得函数关系式为二次函数．那么，此问题可归结为：自变量x为何值时函数y取得最大值？你能解决吗?  实践与探索1      例1．求下列函数的最大值或最小值．（1）；（2）．分析  由于函数和的自变量x的取值范围是全体实数，所以只要确定它们的图象有最高点或最低点，就可以确定函数有最大值或最小值．可通过配方法实现。（解：（1）二次函数当时，函数有最小值是．（2）二次函数当时，函数有最大值是）探索  试一试，当2．5≤x≤3．5时，求二次函数的最大值或最小值．  实践与探索2例2．某产品每件成本是120元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间关系如下表：x（元）130150165y（件）705035若日销售量y是销售价x的一次函数，要获得最大销售利润，每件产品的销售价定为多少元？此时每日销售利润是多少？分析  日销售利润=日销售量×每件产品的利润，因此主要是正确表示出这两个量． 小结与作业回顾与反思     最大值或最小值的求法，第一步确定a的符号，a＞0有最小值，a＜0有最大值；第二步配方求顶点，顶点的纵坐标即为对应的最大值或最小值． 课堂作业：如图26．2．8，在Rt⊿ABC中，∠C=90°，BC=4，AC=8，点D在斜边AB上，分别作DE⊥AC，DF⊥BC，垂足分别为E、F，得四边形DECF，设DE=x，DF=y．（1）用含y的代数式表示AE；（2）求y与x之间的函数关系式，并求出x的取值范围；（3）设四边形DECF的面积为S，求S与x之间的函数关系，并求出S的最大值． 家庭作业：   教学后记