
数学九年级下册6.3 相似图形教案
展开相似图形
一、学习目标:
1、 了解形状相同的图形是相似图形,能在诸多图形中找出相似图形
2、 理解相似三角形、相似多边形、相似比的概念
二、学习重点:相似三角形、相似多边形、相似比的概念。利用概念进行计算和证明。
三、学习难点:证明相似三角形。
四、学习过程:
(一)导入新课:
1.下面五组图形有何特点?
2. 找形状相同的图形.————————形状相同的图形是相似图形。
(二)探索新知:
探索一:(1)度量课本第90页放大镜中的三角形和原三角形对应的角和边,你发现了什么?
(2)放大镜中的三角形和原三角形形状相同吗?它们相似吗?
新知:定义:各角对应相等、各边对应成比例的两个三角形,叫做相似三角形。
相似三角形中对应边的比叫做相似比。
相似用符号“∽”表示,
记作:△ABC∽△A′B′C′,
读作:△ABC相似于△A′B′C ′.
对应边的比如叫做相似比,即k 的值叫做相似三角形的相似比。
试一试
1、分别根据下列已知条件,写出各组相似三角形的对应边的比例式:
①如图1,已知△ADE∽△ABC,则 = =
②如图2,已知△OAB∽△OCD,则 = = _____
③如图3,已知△ABC∽△ACD,则 = =
图1 图2 图3
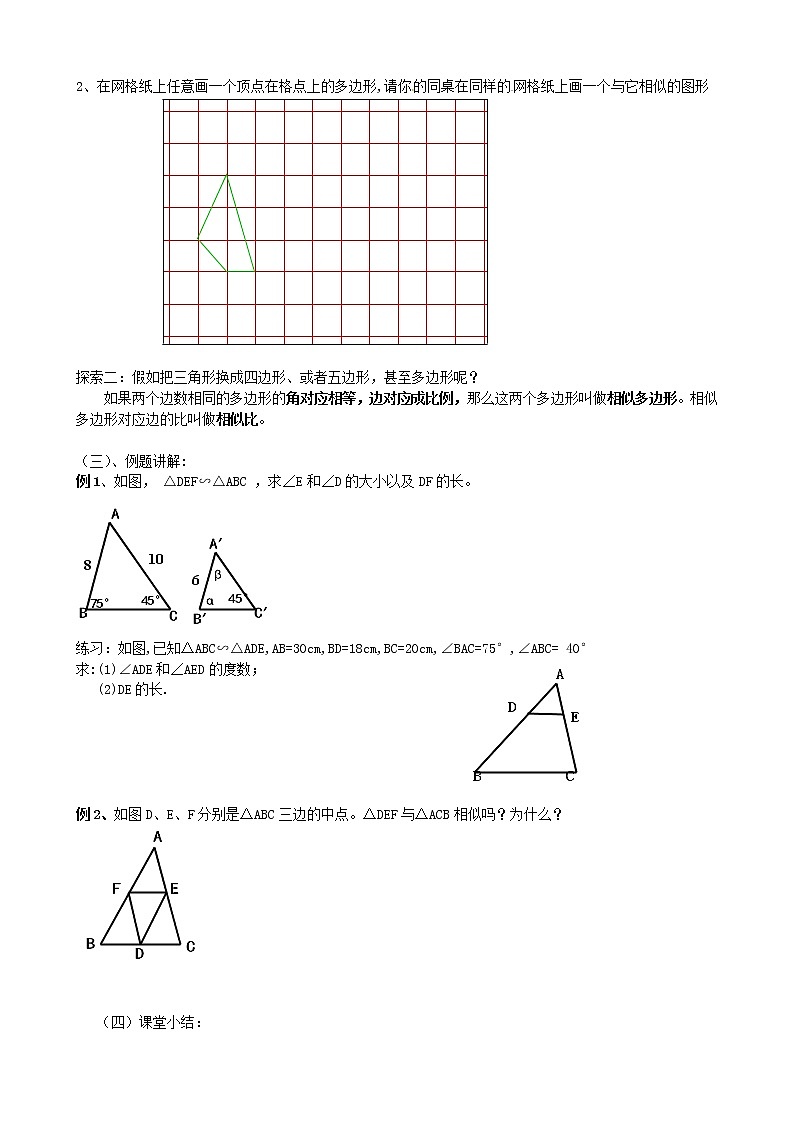
2、在网格纸上任意画一个顶点在格点上的多边形,请你的同桌在同样的网格纸上画一个与它相似的图形
探索二:假如把三角形换成四边形、或者五边形,甚至多边形呢?
如果两个边数相同的多边形的角对应相等,边对应成比例,那么这两个多边形叫做相似多边形。相似多边形对应边的比叫做相似比。
(三)、例题讲解:
例1、如图, △DEF∽△ABC ,求∠E和∠D的大小以及DF的长。
练习:如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°
求:(1)∠ADE和∠AED的度数;
(2)DE的长.
例2、如图D、E、F分别是△ABC三边的中点。△DEF与△ACB相似吗?为什么?
(四)课堂小结:
10.3 相似图形作业 班级 姓名
一、选择题
1.下列说法中,正确的是 ( )
A.任意两个矩形形状相同 B.任意两个菱形形状相同
C.任意两个直角三角形相似 D.任意两个正五边形形状相同
2.已知△ABC∽△A1B1C1,且∠A=50°,∠B=95°,则∠C1的度数为 ( )
A.50° B.95° C.35° D.25°
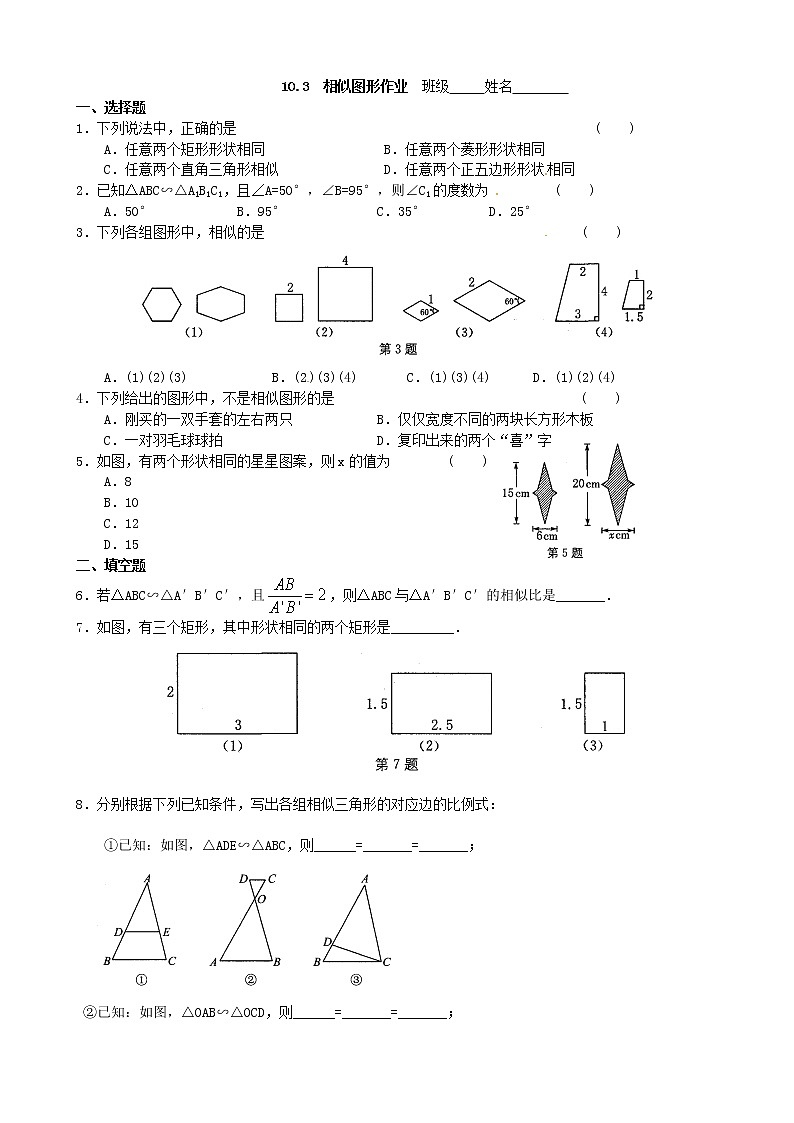
3.下列各组图形中,相似的是 ( )
A.(1)(2)(3) B.(2)(3)(4) C.(1)(3)(4) D.(1)(2)(4)
4.下列给出的图形中,不是相似图形的是 ( )
A.刚买的一双手套的左右两只 B.仅仅宽度不同的两块长方形木板
C.一对羽毛球球拍 D.复印出来的两个“喜”字
5.如图,有两个形状相同的星星图案,则x的值为 ( )
A.8
B.10
C.12
D.15
二、填空题
6.若△ABC∽△A′B′C′,且,则△ABC与△A′B′C′的相似比是_______.
7.如图,有三个矩形,其中形状相同的两个矩形是_________.
8.分别根据下列已知条件,写出各组相似三角形的对应边的比例式:
①已知:如图,△ADE∽△ABC,则______=_______=_______;
②已知:如图,△OAB∽△OCD,则______=_______=_______;
③已知:如图,△ABC∽△ACD,则______=_______=_______.
9.找出两类形状相同的的图形_________、_________.
10.△ABC的三条边的长分别为6、8、10,与△ABC相似的△的最长边为30。则△的最短边的长为_______。△与△ABC的相似比为 。
11.观察一组图形,图形中的三角形都是相似三角形,根据其变化规律,可得第10个图中三角形的个数为
三、解答题
12.下面各组图形中,哪些是相似图形?哪些不是?
13.在右边的网格纸中描出左边图形的缩小图形.
14.在如图所示的两个相似四边形中,求x、y、∠α的值.
15.如图所示,D在AB上,△ADC∽△ACB.(1)写出图中相等的角;(2)写出对应边的比例式;
(3)如果AC=,AD=2,求BD的长。
10.3 相似图形家作 班级 姓名
一、选择填空:
1、下列四组图形中,不一定相似的是 ( )
A.我国国旗上的五角星 B.边长分别为1和2的两个正方形
C.两幅比例尺不同的中国行政地图 D.两个等腰梯形
2、A、B两地的实际距离是200米,画在图上的距离是2厘米,则图上距离与实际距离的比( )
A.1∶10 B.1∶100 C.1∶1000 D.1∶10000
3、在相同时刻的物高与影长成比例.小明的身高为1.5米,在地面上的影长为2米,同一时刻一古塔在地面上的影长为40米 ,则古塔的高位 ( )
A.15 B.10 C.12 D.8
4、我国的报纸都有一个特点:把报纸对折后,所得到的矩形与原矩形相似。这些报纸的长和宽的比值是
A. B. C. D. ( )
5、三角板上分别以内边框和外边框为边的两个三角形_______相似三角形(填是或不是)。
6、(1)写出相似三角形和各组相似三角形的对应边的比例式:如图1,
△ ∽△ ,则____ __=___ ____=______ _;
(2)已知:如图2,△ABC∽△DEF,则这两个三角形的相似比是________.
图2 图1
7、△ABC的各边之比为3:5:7,与其相似的另一个三角形的最长边为28cm,那么它的最小边
为 cm.
8、若△ABC∽△, 且△ABC的三边长分别为,2,,△的两边长分别为,,则其第三边的长为___________.
二、解答题:
1、(1)在下边网格纸中描出第1题图的扩大图形
(2)在右边网格纸中描出第2题图的缩小图形
第1题图 第2题图
2、已知如图中两个梯形相似,求出未知数y,z的长度和∠α,∠β的度数。
3、在图中的△ABC内任取一点M,连结MA、MB、MC,分别取MA、MB、MC的中点A’、B’、C’,连结A’B’、B’C’、C’A’,△ABC和△A’B’C’相似吗?为什么?
拓展与延伸:光明中学要在一块长为60米,宽为30米的矩形场地中心设计一个圆形花坛,半径为5米.求:(1)在比例尺为1:300的平面图上,这个矩形场地的长和宽各是多少?(2)在比例尺1:300的平面图上圆形花坛的面积是多少? (3)矩形场地的实际长宽之比与平面图上的矩形长宽之比分别是多少?它们之间的关系是什么?
初中数学6.3 余角 补角 对顶角教案: 这是一份初中数学6.3 余角 补角 对顶角教案,共2页。教案主要包含了学习目标,学习难点,教学过程等内容,欢迎下载使用。
苏科版七年级上册6.3 余角 补角 对顶角教学设计及反思: 这是一份苏科版七年级上册6.3 余角 补角 对顶角教学设计及反思,共2页。教案主要包含了学习目标,学习难点,教学过程等内容,欢迎下载使用。
苏科版七年级上册第6章 平面图形的认识(一)6.3 余角 补角 对顶角教案: 这是一份苏科版七年级上册第6章 平面图形的认识(一)6.3 余角 补角 对顶角教案,共4页。













