
初中数学苏科版九年级下册6.6 图形的位似教案
展开图形的位似
课型:新授
一、学习目标:
1、通过实验、操作、思考活动认识位似形
2、会利用位似形原理将一个图形放大或缩小。
二、学习过程:
完成下列问题:
1.如图,已知点O和△ABC,画射线OA、OB、OC,在OA、OB、OC上分别取点A′、B′、C′,使
⑴ 画△A′B′C′.,探究△A′B′C′与△ABC的关系.
⑵ 分别在 OA、OB、OC的反向延长线上取点
画△A′′B′′C′′.
- 两个多边形不仅
叫位似图形;这个点叫 .
3通过学习你认为位似图形具有哪些特征呢?
⑴
⑵
⑶
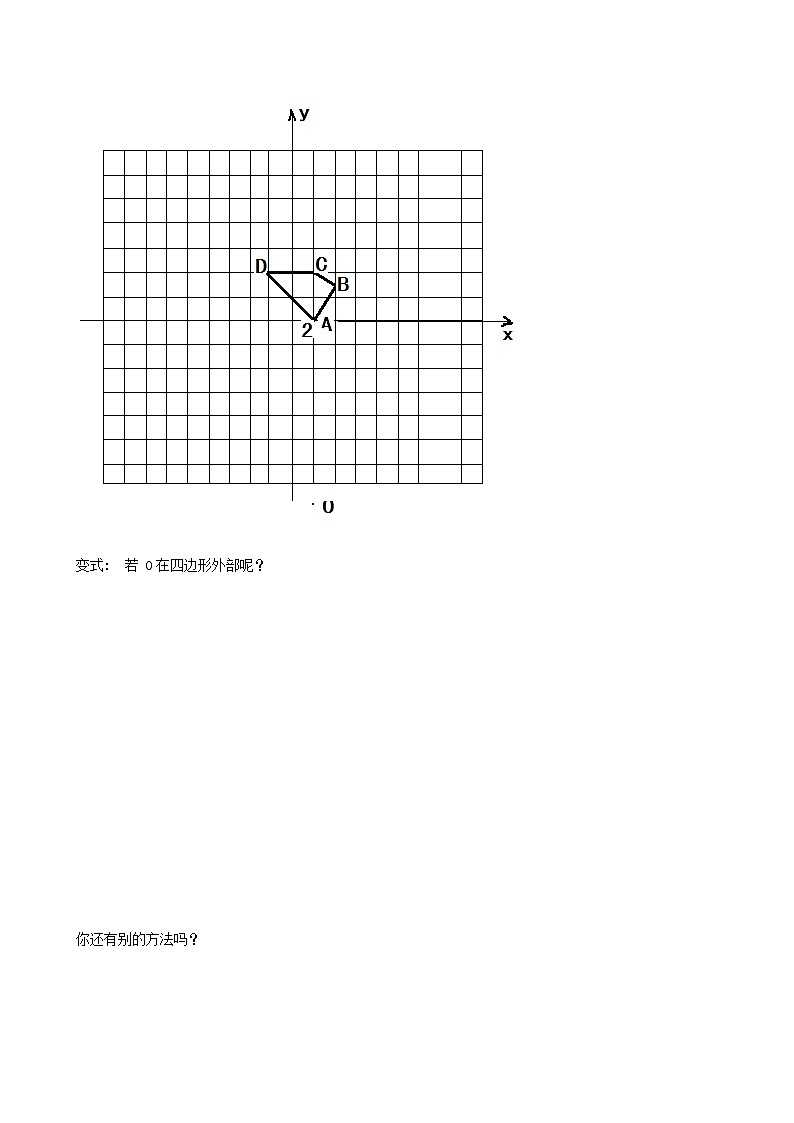
例1、如图,以O为位似中心,将四边形ABCD放大为原来的2倍.
变式: 若 O在四边形外部呢?
你还有别的方法吗?
归理二:如何画?
例2如图(1)请写出四边形ABCD各顶点的坐标;(2)以坐标原点O为位似中心,作四边形ABCD的位似图形,使像与四边形ABCD的位似比为3,求写出像的各顶点的坐标.
归理三:如何求位似图形的点坐标?
以坐标原点为位似中心的位似变换有以下性质:
若原图形上点的坐标为(x,y),像与原图形的位似比为k,则像上的对应点的坐标为 或
§10.6图形的位似课堂作业
班级 姓名
1、用作位似形的方法,可以将一个图形放大或缩小,位似中心( )
(A) 只能选在原图形的外部 (B) 只能选在原图形的内部
(C) 只能选在原图形的边上 (D) 可以选择任意位置
2、下列说法中不正确的是( )
A.位似图形一定是相似图形; B.相似图形不一定是位似图形;
C.位似图形上任意一对对应点到位似中心的距离之比等于相似比;
D.位似图形中每组对应点所在的直线必相互平行
3.按如下方法将△ABC的三边缩小来原来的:如图所示,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法中正确的个数是( )
①△ABC与△DEF是位似图形;
②△ABC与△DEF是相似图形;
③△ABC与△DEF是周长的比为2:1;
④△ABC与△DEF面积比为4:1
A.1个 B.2个 C.3个 D.4个
4、以点O为位似中心,作出四边形ABCD的位似图形,使得新图形与原图形的相似比为2:1.
5、如图,已知五边形A1B1C1D1E1是五边形ABCDE的位似图形,但被小玮擦去了一部分,你能将它补完整吗?
6、已知,在四边形ABCD中,点E为AB上的任一点,过E作EF∥AD交BD于点F,过F作FG∥CD交BC于点G.EG与AC平行吗?为什么?
7.如图△ABC的三个顶点坐标分别为A(2,2) 、B(3,1) 、C(1,0),使将△ABC以O为位似中心放大,使放大后的△DEF与△ABC对应边之比为2:1,并指出其对应边AB与DE有何位置关系?求出点D、E、F的坐标.
8.在AB=30m,AD=20m的矩形ABCD的花坛四周修筑小路.
(1)如果四周的小路的宽均相等,如图(1),那么小路四周所围成的矩形A′B′C′D′和矩形ABCD相似吗?请说明理由.
(2)如果相对着的两条小路的宽均相等,如图(2),试问小路的宽x与y的比值为多少时,能使小路四周所围成的矩形A′B′C′D′和矩形ABCD位似?请说明理由.
§10.6图形的位似家庭作业
班级 姓名
1、关于位似变换:
(1)由位似变换得到的图形与原来的图形是相似图形;
(2)两个图形的对应顶点的连线都经过位似中心;
(3)两个图形的对应边平行或都经过位似中心;
(4)位似中心是可以取在任意位置.上述结论中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
2、(1)如图,正方形ABCD和正方形OEFG中, 点A和点F的坐标分别为(3,2),
(-1,-1),则两个正方形的位似中心的坐标是_________.
(2)如图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,且PA1=PA,则AB׃A1B1等于( )
A、 B、 C、 D、
3、如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为
(a,b),那么大“鱼”上对应“顶点”的坐标为( )
A、(-a,-2b) B、(-2a,-b) C、(-2a,-2b)D、(-2b,-2a)
4、如图,已知△EFH和△MNK是位似图形,那么其位似中心是点 (填A、B、C、D).
5、如图,以A为位似中心,将五角星缩小为原来的.(使对应点在点O的同侧)
6、如图,在直角坐标系中点A的坐标为A(2,3),点B的坐标为B(3,0)。 以O为位似中心,按比例尺2∶1将△AOB放大为△A′O′B′。画出△A′O′B′并写出顶点A′、B′的坐标。
7、如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1).
(1)以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
(2)分别写出B、C两点的对应点B′、C′的坐标;
(3)如果△OBC内部一点M的坐标为(a,b),写出M的对应点M′的坐标.
8、如图,在12×12的正方形网格中,△TAB 的顶点坐标分别为T(1,1)、A(2,3)、
B(4,2).
(1)以点T(1,1)为位似中心,按比例尺(TA′∶TA)3∶1在位似中心的同侧将
△TAB放大为△TA′B′,放大后点A、B的对应点分别为A′、B′.画出△TA′B′,并写出点A′、B′的坐标;
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标.
初中沪科版22.4 图形的位似变换教案设计: 这是一份初中沪科版22.4 图形的位似变换教案设计,共3页。
初中数学苏科版七年级上册6.2 角教案: 这是一份初中数学苏科版七年级上册6.2 角教案,共2页。教案主要包含了学习目标,学习难点,教学过程等内容,欢迎下载使用。
初中第6章 平面图形的认识(一)6.5 垂直教学设计: 这是一份初中第6章 平面图形的认识(一)6.5 垂直教学设计,共4页。