






初中数学1.2.4 绝对值课前预习ppt课件
展开1.理解绝对值的概念及其几何意义.2.会求一个数(不涉及字母)的绝对值.3.会求绝对值已知的数. 4.了解绝对值的非负性,并能用其非负性解决相关问题.
1.什么叫做相反数?
2.你能找出互为相反数的两个数在数轴上表示的点的共同特点吗?
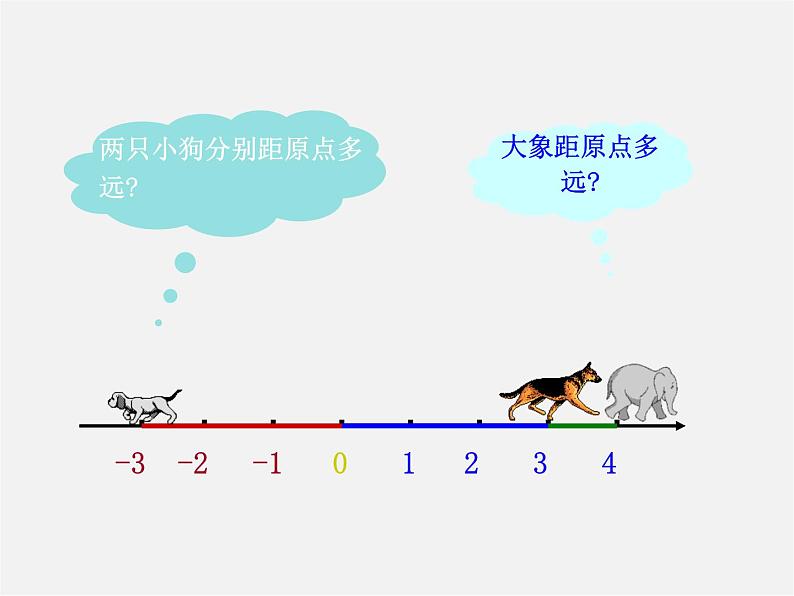
一般地,数轴上表示数 的点与原点的距离叫做数 的绝对值,记作| | .
例如,上面的问题中,在数轴上表示数-1的点和表示数1的点与原点的距离都是1,所以,1与-1的绝对值都是1,即|1|=1,|-1|=1.
练习1:-2的绝对值表示它离原点的距离是 个单位,记作 .练习2:-0.8的绝对值是 .练习3:口答: (1)|+6|= ,| |= , |8.2|= ;(2)|0|= ;(3)|-3|= ,|- |= , |-0.6|= .
数 的绝对值的一般规律: 1.一个正数的绝对值是它本身;
即 ①若 >0,则| |= ; ②若 <0,则| |=– ; ③若 =0,则| |=0.
2.一个负数的绝对值是它的相反数;
1.有没有绝对值等于-2的数? 一个数的绝对值会是 负数吗?为什么?不论有理数 取何值,它的绝 对值总是什么数?
不论有理数 取何值,它的绝对值总是正数或0,即对任意有理数 ,总有 ≥0.
2.互为相反数的两个数的绝对值有什么关系?
一对相反数虽然分别在原点两边,但它们到原点的距离是相等的.所以互为相反数的两个数的绝对值相等.
例1 求下列各数的绝对值.-19, ,0,-2.3,+0.56,-6,+6, .
【解析】-19的绝对值是19,即|-19|=19;
的绝对值是 ,即| |= ;
0的绝对值是0,即|0|=0;
-2.3的绝对值是2.3,即|-2.3|=2.3;
+0.56的绝对值是0.56,即|+0.56|=0.56;
-6的绝对值是6,即|-6|=6;
+6的绝对值是6 ,即|+6|=6;
的绝对值是 ,即| |= .
例2 求下列各数的值.
负数的绝对值是它的相反数
议一议:上述各数的绝对值与这些数本身有什么关系?
正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0.
小组之间讨论一下: (1)当a是正数时,|a|=____; (2)当a是负数时,|a|=__; (3)当a=0时,|a|=___.
1.说出下列各式的值
2.求下列各数的绝对值
9 , -9 , -3.9 , 3.9, , , 0.
答案: 1.26 0
答案:9 9 3.9 3.9 0
1.判断:(1)一个数的绝对值是 2 ,则这个数是2 ( ) (2)|5|=|-5| ( ) (3)|-0.3|=|0.3| ( ) (4)|3|>0 ( ) (5)|-1.4|>0 ( ) (6)有理数的绝对值一定是正数 ( ) (7)若a=b,则|a|=|b| ( ) (8)若|a|=|b|,则a=b ( ) (9)若|a|=-a,则a必为负数 ( ) (10)互为相反数的两个数的绝对值相等 ( )
2.如果a与1互为相反数,则︱a︱等于( ) A.2B.-2C.1D.-1 【解析】选C.1的相反数是-1, ︱-1︱=1.
3.―|―3|=( )A.―3 B.― C. D.3【解析】选A.︱-3︱=3,-︱-3︱=-3.
数轴上表示数a的点与原点的距离
(1)如果a>0,那么|a|=a(2)如果a<0,那么|a|=-a(3)如果a=0,那么|a|=0
初中数学人教版七年级上册1.2.4 绝对值说课ppt课件: 这是一份初中数学人教版七年级上册1.2.4 绝对值说课ppt课件,共12页。PPT课件主要包含了学前温故,新课早知等内容,欢迎下载使用。
七年级上册1.2.4 绝对值教学演示ppt课件: 这是一份七年级上册1.2.4 绝对值教学演示ppt课件,共30页。PPT课件主要包含了做一做,想一想,课堂升华,试一试等内容,欢迎下载使用。
初中数学人教版七年级上册1.2.4 绝对值课前预习ppt课件: 这是一份初中数学人教版七年级上册1.2.4 绝对值课前预习ppt课件,共11页。PPT课件主要包含了绝对值的意义的学习,有理数的大小比较,例题1,绝对值的非负性,例题2,即a1b2,又c0d-1,绝对值的拓展应用,例题3,-a+2b-c等内容,欢迎下载使用。













