_2021年中考一轮复习课件3.3　反比例函数

这是一份_2021年中考一轮复习课件3.3　反比例函数，共60页。
考点一　反比例函数的图象与性质
1.(2020辽宁营口,5,3分)反比例函数y= (xy2>y3　    D.y3>y1>y2
答案    A    ∵k0时,y随x的增大而增大且y0,∴y3y1>y3,故选A.
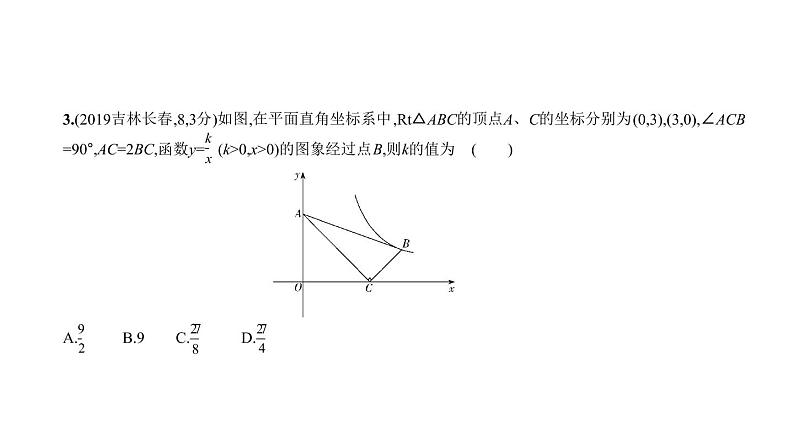
3.(2019吉林长春,8,3分)如图,在平面直角坐标系中,Rt△ABC的顶点A、C的坐标分别为(0,3),(3,0),∠ACB =90°,AC=2BC,函数y= (k>0,x>0)的图象经过点B,则k的值为 (　　) A. 　    B.9　    C. 　    D. 
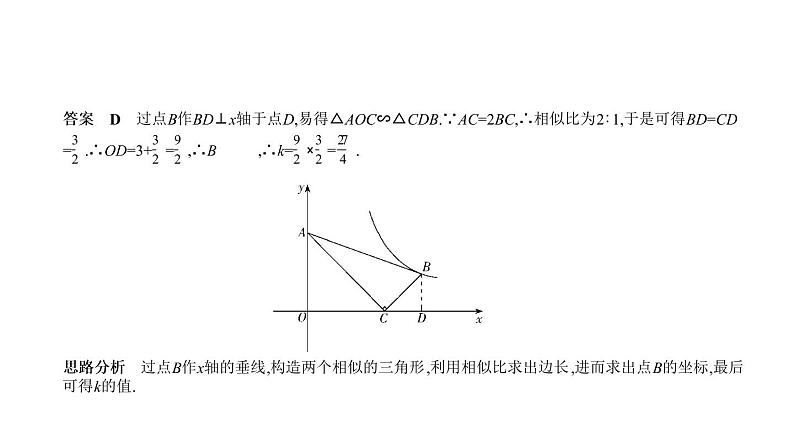
答案    D　过点B作BD⊥x轴于点D,易得△AOC∽△CDB.∵AC=2BC,∴相似比为2∶1,于是可得BD=CD = .∴OD=3+ = ,∴B ,∴k= × = . 
思路分析　过点B作x轴的垂线,构造两个相似的三角形,利用相似比求出边长,进而求出点B的坐标,最后 可得k的值.
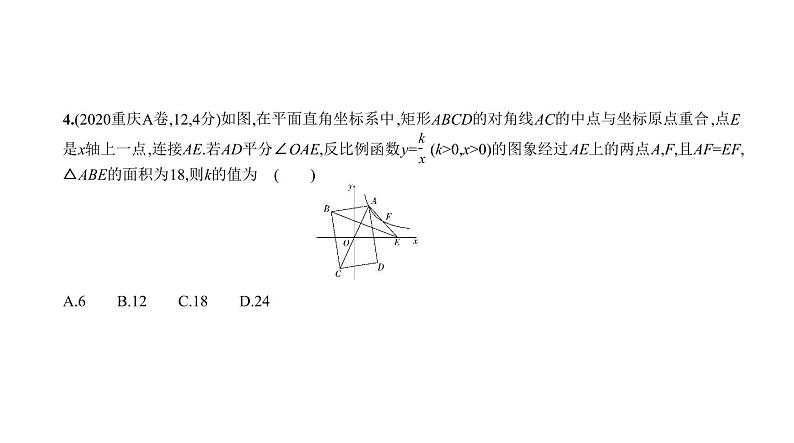
4.(2020重庆A卷,12,4分)如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E 是x轴上一点,连接AE.若AD平分∠OAE,反比例函数y= (k>0,x>0)的图象经过AE上的两点A,F,且AF=EF,△ABE的面积为18,则k的值为 (　　) A.6　    B.12　    C.18　    D.24
答案    B　连接BD,∵AD平分∠OAE,∴∠OAD=∠EAD,∵四边形ABCD是矩形,∴OA=OD,∴∠ODA=∠ OAD,∴∠ODA=∠EAD,∴BD∥AE,∴△AOE与△ABE的面积相等,为18,又∵AF=EF,∴△OEF的面积为 9,设F ,∵F为AE的中点且A点在反比例函数y= (k>0,x>0)的图象上,∴A ,过A作AM⊥x轴于M,过F作FN⊥x轴于N,则OM= ,MN= ,又∵AF=EF,∴MN=NE,∴△OFN的面积为△OEF面积的 ,为6,∴k=2S△OFN=12. 
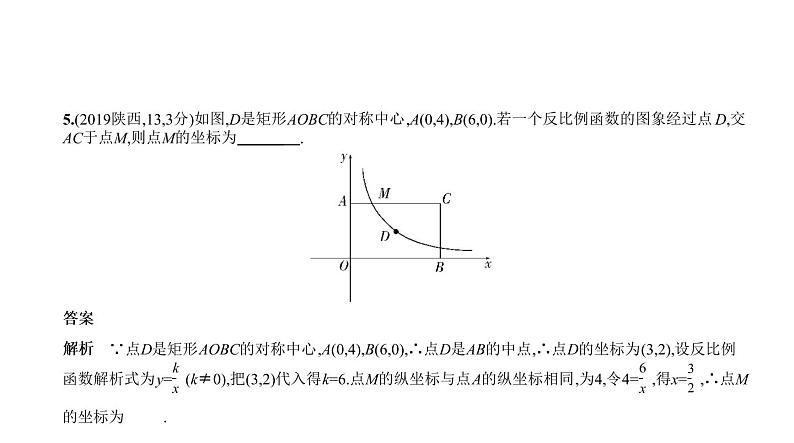
5.(2019陕西,13,3分)如图,D是矩形AOBC的对称中心,A(0,4),B(6,0).若一个反比例函数的图象经过点D,交 AC于点M,则点M的坐标为　　　    .
6.(2019内蒙古包头,19,3分)如图,在平面直角坐标系中,已知A(-1,0),B(0,2),将△ABO沿直线AB翻折后得 到△ABC,若反比例函数y= (x0)的图象上(点B的横坐标大于点A的横坐标),点A的坐标为(2,4),过点A作AD⊥x轴于点D,过点B作BC⊥x轴于点C,连接OA,AB.(1)求k的值;(2)若D为OC的中点,求四边形OABC的面积. 
解析　(1)把(2,4)代入y= ,得4= .解得k=8. (3分)(2)∵点A的坐标是(2,4),∴OD=2,AD=4.∵D为OC的中点,∴OC=2OD=4. (4分)当x=4时,y= =2,∴点B的坐标是(4,2),∴BC=2. (5分)∴S四边形OABC=S△AOD+S四边形ABCD= ×2×4+ ×(2+4)×2=10.
∴四边形OABC的面积是10. (7分)
思路分析　(1)将点A的坐标代入y= ,可得k值;(2)将点C的横坐标代入反比例函数的解析式可得点B的纵坐标,利用三角形和梯形的面积公式可得结果.
8.(2020江西,18,8分)如图,Rt△ABC中,∠ACB=90°,顶点A,B都在反比例函数y= (x>0)的图象上,直线AC⊥x轴,垂足为D,连接OA,OC,并延长OC交AB于点E,当AB=2OA时,点E恰为AB的中点,若∠AOD=45°,OA=2  .(1)求反比例函数的解析式;(2)求∠EOD的度数. 
解析　(1)∵AD⊥x轴,∠AOD=45°,OA=2 ,∴AD=OD=2.∴A(2,2).∵点A在反比例函数图象上,∴k=2×2=4.∴y= .(2)∵△ABC为直角三角形,点E为AB的中点,∴AE=CE=EB,∴∠AEC=2∠ECB.∵AB=2OA,∴AO=AE.∴∠AOE=∠AEO=2∠ECB.∵∠ACB=90°,AD⊥x轴,∴BC∥x轴.
∴∠ECB=∠EOD.∴∠AOE=2∠EOD.∵∠AOD=45°,∴∠EOD= ∠AOD= ×45°=15°.
9.(2019甘肃兰州,23,7分)如图,在平面直角坐标系xOy中,反比例函数y= (k≠0)的图象过等边三角形BOC的顶点B,OC=2,点A在反比例函数图象上,连接AC,AO.(1)求反比例函数y= (k≠0)的表达式;(2)若四边形ACBO的面积是3 ,求点A的坐标. 
解析　(1)∵OC=2,且△BOC为等边三角形,∴B(-1,- ),∴k=(-1)×(- )= ,∴反比例函数表达式为y= .(2)S四边形ACBO=S△BOC+S△AOC,过点A作AN⊥x轴于点N.∵S△BOC= OC2= ,∴ +S△AOC=3 ,∴S△AOC=2 ,即 OC·AN=2 ,又∵OC=2,∴AN=2 ,设A(t,2 ),∴2 t= ,∴t= ,即点A的坐标为 .
考点二　反比例函数与一次函数的综合应用
1.(2020宁夏,7,3分)如图,函数y1=x+1与函数y2= 的图象相交于点M(1,m),N(-2,n).若y1>y2,则x的取值范围是 (　　) A.x1),分别与直线y=kx+2和双曲线y= 交于P、Q两点,且PQ=2QD,求点D的坐标.
解析　(1)把(-1,0)代入y=kx+2,得-k+2=0,解得k=2,∴一次函数解析式为y=2x+2.把(1,n)代入y=2x+2,得n=4,∴C(1,4),把(1,4)代入y= ,得m=1×4=4,∴反比例函数解析式为y= .(2)∵PD∥y轴,D(a,0),∴P(a,2a+2),Q ,∵PQ=2QD,∴2a+2- =2× ,整理得a2+a-6=0,解得a1=2,a2=-3(舍去),经检验,a=2为原分式方程的解,且符合题意,∴D(2,0).
11.(2019云南昆明五华模拟,20)已知反比例函数y= (a为常数)的图象经过点B(-4,2).(1)求a的值;(2)如图,过点B作直线AB与函数y= 的图象交于点A,与x轴交于点C,且AB=3BC,过点A作直线AF⊥AB,交x轴于点F,求线段AF的长. 
解析　(1)将(-4,2)代入y= ,得2= ,解得a=-12.(2)∵a=-12,∴反比例函数解析式为y=- ,分别过点B、A作x轴的垂线,垂足分别为点D、E,则BD=2.∵AB=3BC,∴ = .由作图知BD∥AE,∴△BCD∽△ACE,∴ = ,即 = ,∴AE=8.把y=8代入y=- ,得x=-1.∴A(-1,8).设直线AB的解析式为y=kx+b(k≠0),把(-1,8),(-4,2)代入解析式得, 解得 ∴直线AB的解析式为y=2x+10,当y=0时,2x+10=0,解得x=-5,∴C(-5,0),