人教版七年级下册5.3.1 平行线的性质图片课件ppt

这是一份人教版七年级下册5.3.1 平行线的性质图片课件ppt，共19页。PPT课件主要包含了课件说明，答BE∥CF，归纳小结等内容，欢迎下载使用。
学习目标：（1）平行线的性质与判定的应用．（2）经历例题的分析过程，从中体会转化的思想和分析问题的方法，进一步培养推理能力，体会数学在实际生活中的应用．学习重点：综合应用平行线的性质与判定解决问题．
1．梳理旧知，引入新课
问题1 （1）平行线的性质是什么？
　性质1 两直线平行，同位角相等．
性质2 两直线平行，内错角相等．
性质3 两直线平行，同旁内角互补．
这三个性质中条件和结论分别是什么？
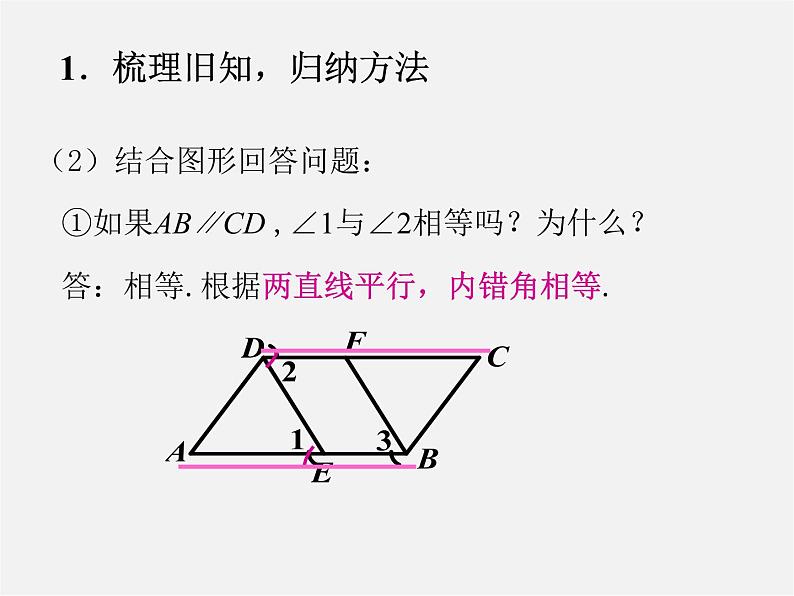
（2）结合图形回答问题：
答：相等.根据两直线平行，内错角相等.
1．梳理旧知，归纳方法
①如果AB∥CD ,∠1与∠2相等吗？为什么？
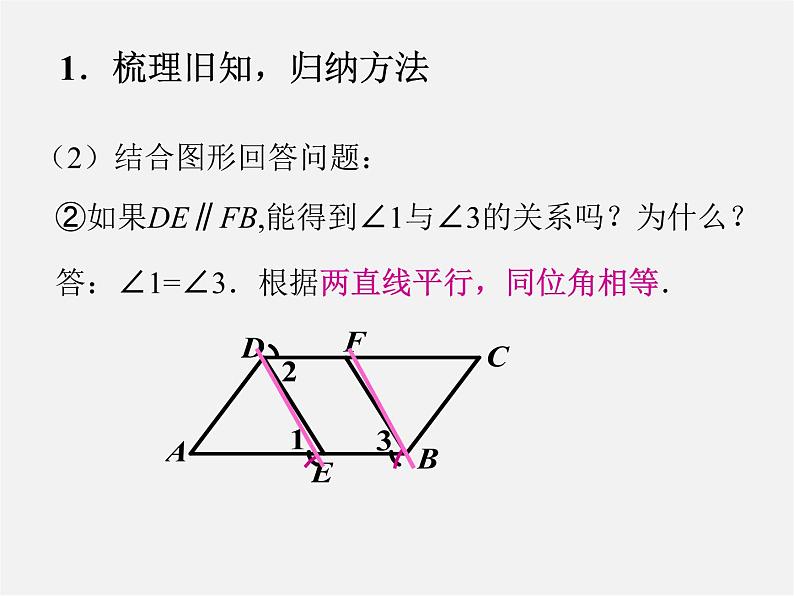
答：∠1=∠3．根据两直线平行，同位角相等．
②如果DE∥FB,能得到∠1与∠3的关系吗？为什么？
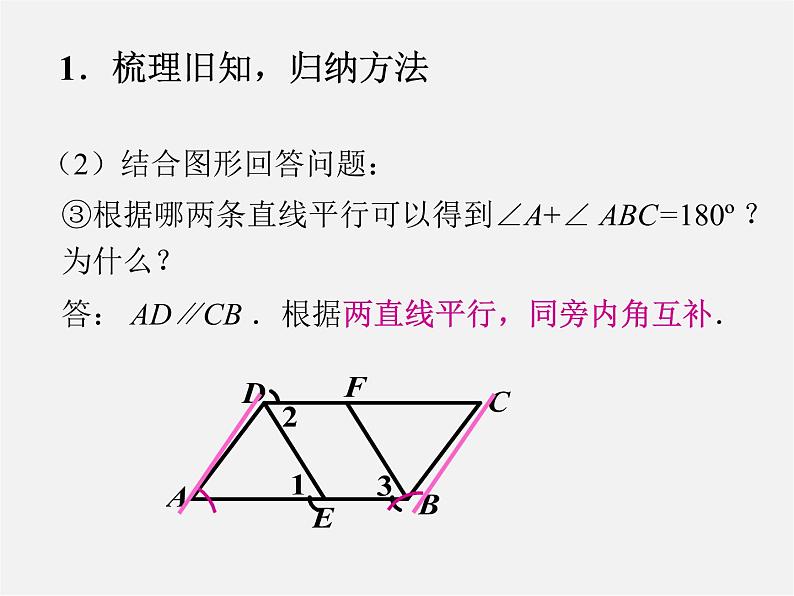
答： AD∥CB ．根据两直线平行，同旁内角互补．
③根据哪两条直线平行可以得到∠A+∠ ABC=180º ？为什么？
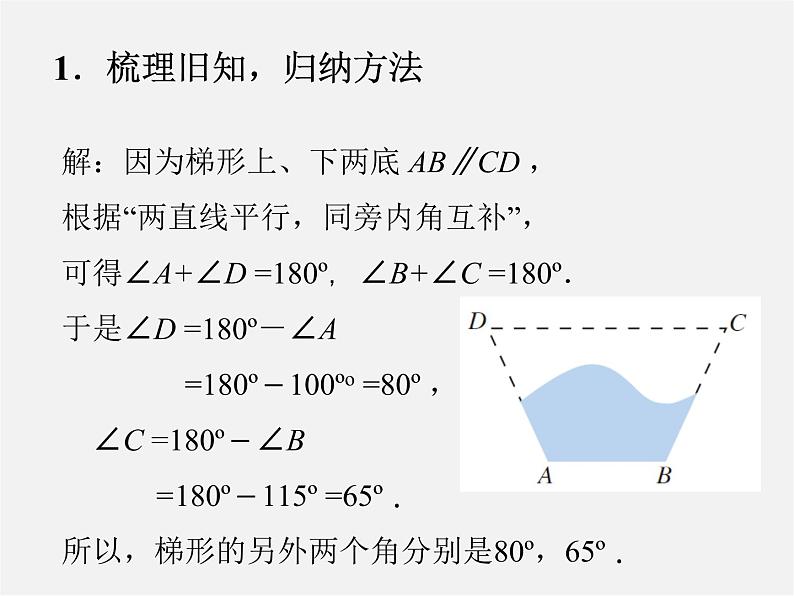
问题2 如图，是一块梯形铁片的残余部分，量得∠A=100º，∠B=115º，梯形的另外两个角分别是多少度？
解：因为梯形上、下两底 AB∥CD ，根据“两直线平行，同旁内角互补”，可得∠A+∠D =180º，∠B+∠C =180º．于是∠D =180º－∠A =180º－100º =80º ， ∠C =180º－∠B =180º－115º =65º ．所以，梯形的另外两个角分别是80º，65º ．
问题3 对比平行线的性质和判定方法，你能说出它们的区别吗？
理由如下：∵ CE∥BF，∴∠1=∠B．∵∠1=∠2 ，∴∠2=∠B．∵∠2和∠B是内错角，∴ AB∥CD（内错角相等，两直线平行）．
2．综合运用，巩固提高
问题4 已知，如图，∠1=∠2，CE∥BF，试说明： AB∥CD．
练习1　如图，AB∥CD，BE平分∠ABC，CF平分∠BCD，你能发现BE与CF的位置关系吗？说明理由．
理由如下：∵ BE平分∠ABC，∴同理∵ AB∥CD，∴∠ABC=∠BCD.∴∠1=∠2.∵∠1和∠2是内错角，∴ BE∥CF（内错角相等，两直线平行）.
练习2　已知：如图，∠AGD=∠ACB，∠1=∠2，CD与EF平行吗？为什么？
理由如下：∵ ∠AGD =∠ACB ，∴ GD∥BC. ∵∠1和∠3是内错角，∴∠1=∠3（两直线平行,内错角相等）.∵∠1=∠2，∴∠2=∠3.∵∠2和∠3是同位角，∴ CD∥EF（同位角相等，两直线平行）.
3．应用迁移，拓展升华
问题5 如图，潜望镜中的两面镜子是互相平行放置的，光线经过镜子反射时，∠1=∠2，∠3=∠4，∠2和∠3有什么关系？为什么进入潜望镜的光线和离开潜望镜的光线是平行的？
已知条件：如图，AB∥CD，∠1=∠2，∠3=∠4．猜想：∠2和∠3有什么关系，并说明理由；试说明：PM∥NQ．
答：∠2=∠3.理由如下：∵ AB∥CD ，∴ ∠2=∠3（两直线平行，内错角相等）．
已知条件：如图，AB∥CD，∠1=∠2，∠3=∠4．试说明：PM∥NQ．
理由如下：∵∠1=∠2 ，∠3=∠4，又∵∠2=∠3．∴∠1=∠2 =∠3=∠4．∵∠1+∠2 +∠5=180º，∠3+∠4 +∠6=180º，∴∠5=∠6．∵∠5和∠6是内错角，∴ PM∥NQ （内错角相等，两直线平行）．
（1）平行线的性质与判定的区别是什么？
（2）在解决具体问题过程中，你能区别什么时候需要使用平行线的性质，什么时候需要使用平行线的判定吗？