初中数学人教版七年级下册5.2.2 平行线的判定教课ppt课件

这是一份初中数学人教版七年级下册5.2.2 平行线的判定教课ppt课件，共18页。PPT课件主要包含了创设情景明确目标，合作探究达成目标，总结梳理内化目标，达标检测反思目标等内容，欢迎下载使用。

如图所示，装修工人正在向墙上钉木条，如果木条b与墙壁的边缘垂直，那么木条a与墙壁的边缘所夹的角为多少度时，才能使木条a与木条b平行？
掌握平行线的三种判定方法；
能够灵活运用平行线的三种判定方法进行推理和计算。
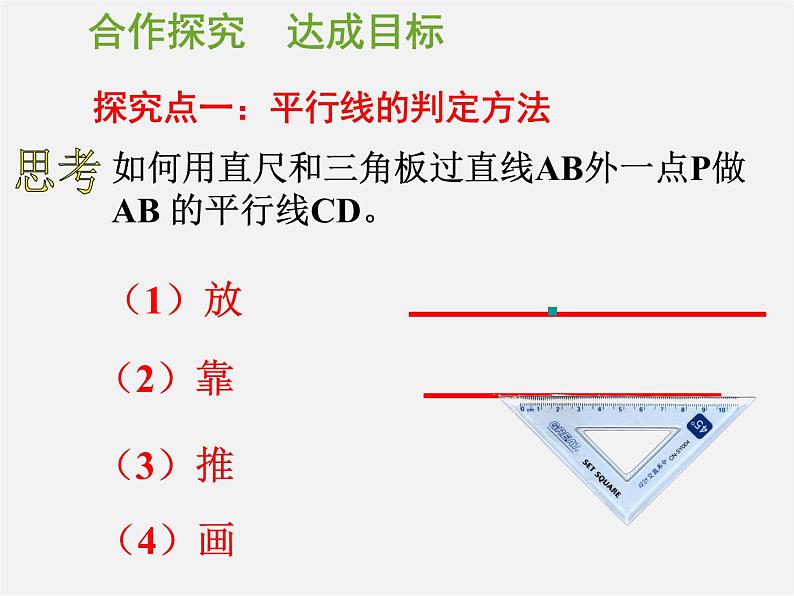
探究点一：平行线的判定方法
如何用直尺和三角板过直线AB外一点P做AB 的平行线CD。
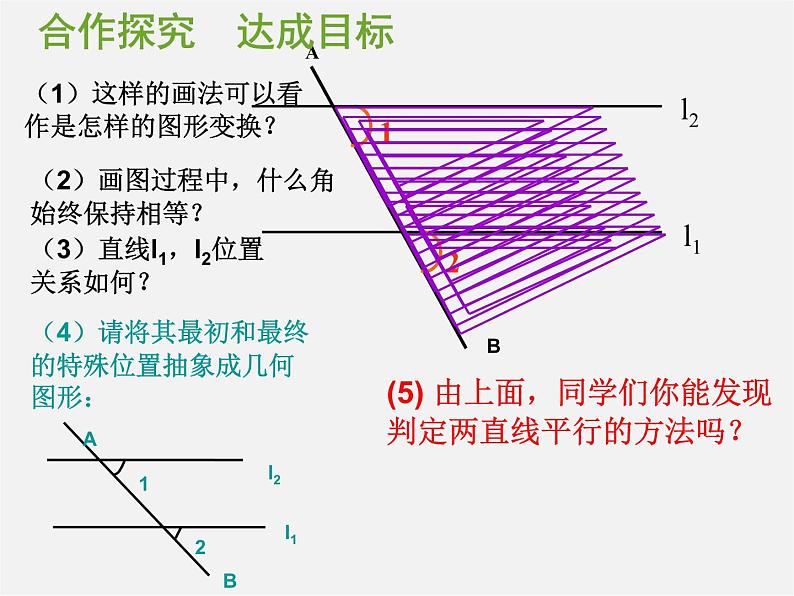
（1）这样的画法可以看作是怎样的图形变换？
（4）请将其最初和最终的特殊位置抽象成几何图形：
（2）画图过程中，什么角始终保持相等？
（3）直线l1，l2位置关系如何？
(5) 由上面，同学们你能发现判定两直线平行的方法吗？
一般地，判定两直线平行有以下的方法：
两条直线被第三条所截，如果同位角相等，那么这两条直线平行．简单地说，同位角相等，两直线平行．
∵∠1=∠2（已知）∴a∥b（同位角相等，两直线平行）
两条直线被第三条直线所截，同时得到同位角、内错角和同旁内角，由同位角相等可以判定两直线平行，那么，能否利用内错角和同旁内角来判定两直线平行呢？
如图，由3= 2，可推出a//b吗？如何推出？写出你的推理过程。
∵1=3(已知） 3= 2（对顶角相等）  1= 2  a//b(同位角相等，两直线平行）
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行简单说成：内错角相等,两直线平行
如图，直线a、b被直线c所截， 若∠2+∠3=180°， 则a b
答：∵ ∠2+∠3=180°(已知) ∠1+∠3=180°(邻补角定义) ∴ ∠1=∠2 (同角的补角相等) ∴a∥b(同位角相等，两直线平行)
判定方法3 同旁内角互补，两直线平行.
探究点二：平行线判定的应用
木工师傅用角尺画出工件边缘的两条垂线，就可以再找出两条平行线，如图所示，a∥b，你能说明是什么道理吗？
解 ∵∠1=∠2=90° ∴a∥b（同位角相等，两直线平行）
例：在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线平行吗？为什么？
∵b⊥a,c⊥a. (已知)
如图：b⊥a、c⊥a，那么b、c平行吗？
∴∠1=∠2=90(垂直定义)
∴b∥c.(同位角相等，两直线平行)
1．上交作业：教科书习题5.2第4，7题;2．课后作业: 见“学生用书”的课后测评案 .
1．如图所示，在下列条件中，不能判断L1∥L2的是（ ）． A．∠1=∠3 B．∠2=∠3
C．∠4+∠5=180° D．∠2+∠4=180°
2．如图，BE是AB的延长线。由∠CBE=∠A可以判定____∥___根据是________________________由∠CBE=∠C可以判定___∥____根据是___________________________
同位角相等，两直线平行；
内错角相等，两直线平行.
3．如图，一个弯形管道ABCD的拐角∠ABC=120°，∠BCD=60°，这时说管道AB∥CD吗？请说明理由。
答：AB∥CD，因为同旁内角互补，两直线平行。
4．如图所示，已知∠OEB=130°，∠FOD=25°，OF平分∠EOD，试说明AB∥CD．
解：根据∠OEB+∠EOD=180°得到AB∥CD