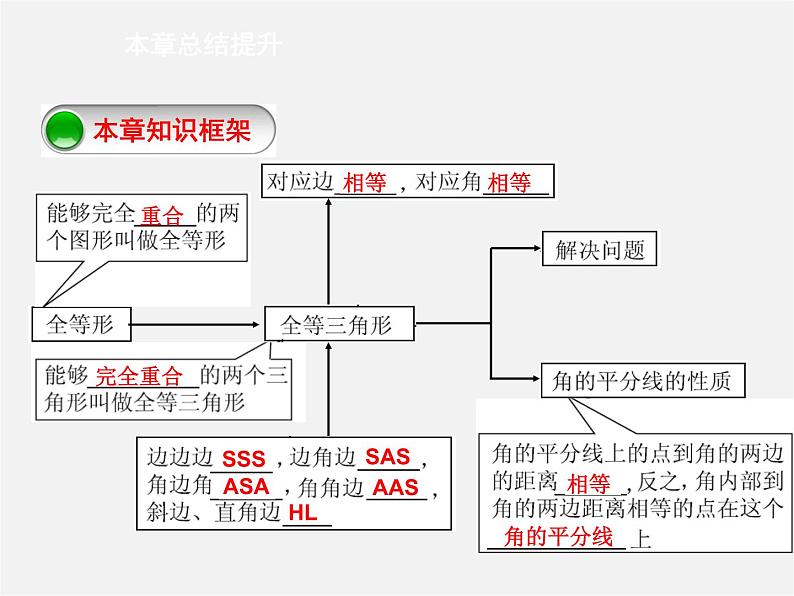
初中数学人教版八年级上册12.1 全等三角形复习ppt课件

这是一份初中数学人教版八年级上册12.1 全等三角形复习ppt课件，共27页。PPT课件主要包含了第十二章全等三角形，本章总结提升，完全重合，SSS，SAS，ASA，AAS，角的平分线，针对训练等内容，欢迎下载使用。

本 章 总 结 提 升
► 类型之一　一元二次方程及有关概念
思想方法：全等变换包括平移变换、翻折变换和旋转变换三种方式.全等变换前后的两个图形全等，具有全等的所有性质，所以利用全等变换是证明线段相等或角相等的基本方法，有时通过全等变换把已知的边（或角）与要证的边（或角）集中在某一个三角形中，便于解决问题.
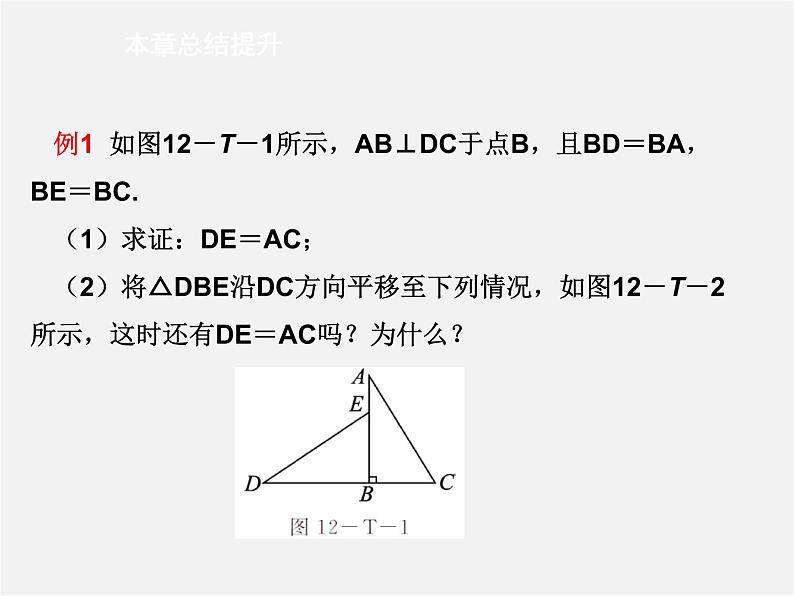
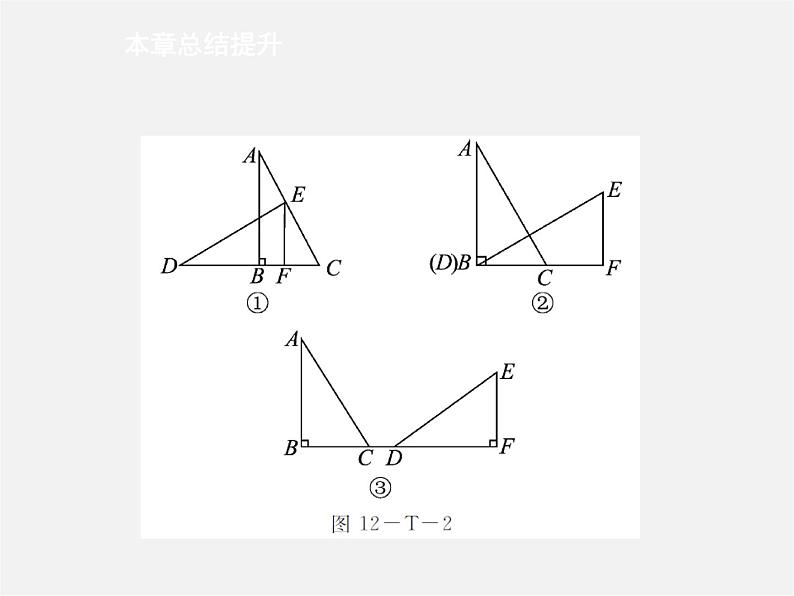
例1 如图12－T－1所示，AB⊥DC于点B，且BD＝BA，BE＝BC.（1）求证：DE＝AC；（2）将△DBE沿DC方向平移至下列情况，如图12－T－2所示，这时还有DE＝AC吗？为什么？
［解析］ （1）要证DE＝AC，只需证它们所在的△DBE和△ABC全等即可；（2）各图均由图12－T－1变化而来，属于全等变换，证明方法都与（1）相同.
［点评］ 注重基本图形的挖掘，平移变换中，线、角的大小关系没有变化，证线段相等，关键还是证两线段所在的两个三角形全等.
1.如图12－T－3所示，在有公共顶点的△ABC和△ADE中，AB＝AC，AD＝AE，且∠CAB＝∠EAD.（1）求证：CE＝BD；（2）若将△ADE绕点A沿逆时针方向旋转，当旋转到点C，E，D在一条直线上时，如图12－T－4所示，（1）问中的结论是否仍然成立？如果成立，请证明；如果不成立，请说明理由.
［解析］ （1）要证CE＝BD，只需证它们所在的△ACE和△ABD全等，结合已知条件易证.（2）由于旋转后△ABC和△ADE形状没有变化，而且∠CAE和∠DAB仍然相等，△ACE和△ABD全等，则结论CE＝BD仍成立.
［点评］ 当完成本题后，可以利用旋转变换、改变图形探究结论是否仍然成立，这有利于培养学生的创新精神和探究问题的能力.
► 类型之二　利用三角形全等证明有关结论
思想方法：全等三角形的对应边相等和对应角相等，所以在平面几何中，证明两线段相等、两个角相等、两条直线互相平行、两条直线互相垂直等问题时，常常可以通过证明三角形全等来实现.有时在整个证明过程中往往要完成多次三角形全等的证明，才能解决待证（或待求）的问题.
例2 如图12－T－5所示，AB＝DC，AD＝BC，DE＝BF.求证：BE＝DF.
［解析］ BE和DF分别在△ABE与△CDF（或△BDE与△DBF）中，由已知条件不能直接推导它们全等，结合图形，连接BD，可证△ABD≌△CDB，得∠A＝∠C，再去证△ABE≌△CDF.
［点评］ （1）当条件不足时，常常通过添加辅助线得出新的条件，进一步完成问题的解答.（2）连接四边形的对角线，把四边形问题转化为三角形问题来解决，是数学常用的方法，它可使复杂问题简单化，并能够较清晰地找到边的关系.
2.如图12－T－6所示，在四边形ABCD中，BC>BA，AD＝CD，BD平分∠ABC.求证：∠A＋∠C＝180°.
证明：在BC上截取BE＝AB，连接DE.易证△ABD≌△EBD，∴AD＝ED，∠A＝∠BED.过点D作DF⊥EC于点F.
∵AD＝CD，∴DE＝DC.又DF＝DF，∴Rt△DEF≌Rt△DCF，∴∠C＝∠DEC.∴∠A＋∠C＝∠BED＋∠DEC＝180°.
► 类型之三　利用角平分线的性质（或判定）证明有关结论
思想方法：角的平分线不仅把角分成相等的两部分，而且角的平分线上的点到角两边的距离相等，以及到角两边距离相等的点在这个角的平分线上，这些为我们证明线段（或角）相等提供了便利的方法.
［解析］ 作ME⊥AD，证△AME≌△AMB.
证明：（1）过点M作ME⊥AD于点E.∵DM平分∠ADC，∠C＝90°，∴MC＝ME.∵M是BC的中点，∴MC＝MB＝ME.又AM＝AM，∠AEM＝∠ABM＝90°，∴Rt△BAM≌Rt△EAM（HL），∴∠EAM＝∠BAM，即AM平分∠DAB.
［点评］ 作出点M到角两边的距离，利用距离相等是解决这个问题的关键，因此当遇到角平分线的问题时，如果不能打开思路，不妨过角平分线上的点作出到角两边的垂线.
3.如图12－T－8所示，已知∠B＝∠E＝90°，CE＝CB，AB∥CD.求证：AD＝CD.
► 类型之四　运用三角形全等解决生活实际问题
思想方法：全等三角形广泛应用于现实生活中，为我们解决实际问题提供了有力的工具.把实际问题转化为数学问题，抽象概括出基本的几何图形，并充分利用所学知识构造全等三角形，利用全等三角形的性质解决问题.
例4 如图12－T－9所示，要测量池宽，可从点A出发在地面上画一条线段AC，使AC⊥AB，再从C点观测，在BA的延长线上测得一点B′，使∠ACB′＝∠ACB.这时量得的AB′的长度就是AB的长度.请按图写出已知、求证，并加以证明.
4.一位经历过战争的老人讲述了这样一个故事：在一次战役中，我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡，需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下，一个战士想出来这样一个办法：他面向碉堡的方向站好，然后调整帽子，使视线通过帽檐正好落在碉堡的底部；然后，他转过一个角度，保持刚才的姿态，这时视线落在了自己所在岸的某一点上；接着，他用步测的方法量出自己与那个点的距离，这个距离就是他与碉堡间的距离.请解释其中的道理.