冀教版九年级下册29.3 切线的性质和判定课前预习ppt课件

这是一份冀教版九年级下册29.3 切线的性质和判定课前预习ppt课件，共23页。PPT课件主要包含了学习目标，一起探究学习新课，新课学习，几何语言，∴l⊥OA，巩固小练习，OA为⊙O的半径，∵BC⊥OA于A，∴BC为⊙O的切线，切线的判定等内容，欢迎下载使用。

1.判定一条直线是否是圆的切线并会过圆上一点作圆的切线.2.理解并掌握圆的切线的性质定理及判定定理.3.能运用圆的切线的性质定理和判定定理解决问题.
创设问题情境，引入新课
直线行驶的自行车车轮与车印是什么关系呢？
今天我们就来探究一下直线与圆相切时，会有哪些性质..
思考：如图，如果直线l是⊙O 的切线，点A为切点，观察OA与直线l的位置关系可能是什么？
OA与直线l要么垂直,要么不垂直.
（1）假设OA与l不垂直,作OM⊥l于点M.
（2）则OM（3）所以OA与l垂直.
∵直线l与⊙O 相切于点A.
一、切线性质 圆的切线垂直于经过切点的半径．
1.如图，PA为⊙O的切线，切点为A，OP=2，∠APO=45°,则⊙O的半径=____.图中阴影面积=______.
辅助线：连接圆心和切点
2.如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=120°，过D点的切线PD与直线AB交于点P，则∠ADP的度数为（ ）A．40° B．35° C．30° D．45°
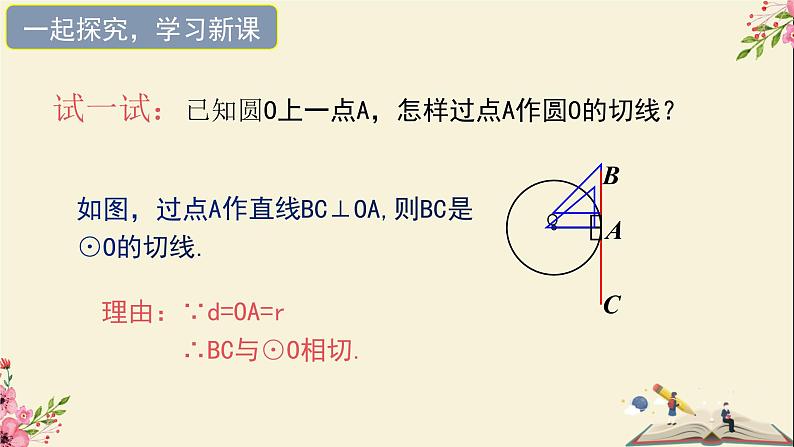
试一试：已知圆O上一点A，怎样过点A作圆O的切线？
如图，过点A作直线BC⊥OA,则BC是⊙O的切线.
理由：∵d=OA=r ∴BC与⊙O相切.
经过半径的外端并且垂直于这条半径的直线是圆的切线.
1.判断下列命题是否正确.⑴ 经过半径外端的直线是圆的切线.⑵ 垂直于半径的直线是圆的切线.⑶ 过直径的外端并且垂直于这条直径的直线是圆的切线.⑷ 和圆只有一个公共点的直线是圆的切线.⑸ 过直径一端点且垂直于直径的直线是圆的切线.
2.下列各直线是不是圆的切线？如果不是，请说明为什么？
因为没有经过半径的外端.
注意：“经过半径的外端”和“垂直于这条半径”，两个条件缺一不可，否则就不是圆的切线.
3.如图所示，A是⊙O上一点，且AO=5,PO=13,AP=12,则PA与⊙O的位置关系是 .
例1.已知：直线AB经过⊙O上的点C，并且OA=OB，CA=CB.求证：直线AB是⊙O的切线.
分析：由于AB过⊙O上的点C，所以连接OC，只要证明AB⊥OC即可.
证明：连接OC. ∵ OA＝OB,CA＝CB, ∴ AB⊥OC.（三线合一） ∵ OC是⊙O的半径, ∴ AB是⊙O的切线.
例2.如图,△ABC 中，AB ＝AC ，O 是BC中点，⊙O 与AB 相切于E.求证：AC 是⊙O 的切线．
分析：由点O向AC作垂线段OF，d=OF,r=OE，因此只需要证明OF=OE.
证明：连接OE，OA,过O作OF⊥AC于点F.
∵⊙O与AB相切于E∴OE ⊥ AB.
∵AB＝AC,O是BC中点．
∵d=OF,r=OE.∴d=r.
又OE⊥AB ，OF⊥AC.
证明直线与圆相切的方法：
1.定义法：和圆有且只有一个公共点的直线是圆的切线;
2.数量关系法：圆心到直线的距离等于半径(即d=r)的直线是圆的切线；
3.判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。
(1) 有交点，连半径,证垂直; (2) 无交点，作垂直,证半径.
已知中有切线时的常用辅助线
见切点，连半径，得垂直.
1.如图所示，已知AB是⊙O的直径，AC,BC是⊙O的弦，OE∥AC交BC于E,过点B作⊙O的切线交OE的延长线于点D,连接DC并延长交BA的延长线于点F.(1)求证：DC是⊙O的切线.(2)若∠ABC=30°,AB=8，求CF.
(1)连接OC,证明△DBO≌△DCO，可得∠DCO=∠DBO=90°
2.如图所示，△ABC内接于⊙O,∠B=60°，CD是⊙O的直径，点P是CD延长线上一点，且AP=AC.(1)求证:PA是⊙O的切线；(2)若PD=2，求⊙O的直径.
(1)连接OA,由题意计算出∠OAP=90°.
(2)在Rt△OAP中，∠P=30°，推出PO=2AO=2DO,则PD=OD.⊙O的直径=2×2=4.
证明：连接OP. ∵AB=AC,∴∠B=∠C. ∵OB=OP，∴∠B=∠OPB， ∴∠OBP=∠C. ∴OP∥AC. ∵PE⊥AC， ∴PE⊥OP. ∴PE为⊙O的切线.
3.如图,△ABC中，AB=AC，以AB为直径的⊙O交边BC于P， PE⊥AC于E. 求证:PE是⊙O的切线.
有交点，连半径，证垂直
无交点，作垂直，证半径