初中数学冀教版九年级下册30.4 二次函数的应用图文课件ppt

这是一份初中数学冀教版九年级下册30.4 二次函数的应用图文课件ppt，共26页。PPT课件主要包含了学习目标，创设情境引入新课，新课学习，归纳总结，函数与方程的关系，巩固练习，∴取x80，典例精析，问题一，问题二等内容，欢迎下载使用。

1.根据题意求出二次函数.2.根据给定的函数值，将二次函数转化为一元二次方程求解.3.根据给定的函数值的范围，将二次函数转化为一元二次不等式或不等式组求解.
汽车在行驶中，由于惯性作用，刹车后还要向前滑行一段距离才能停住，这段距离叫做刹车距离.刹车距离是分析和处理道路交通事故的一个重要因素.
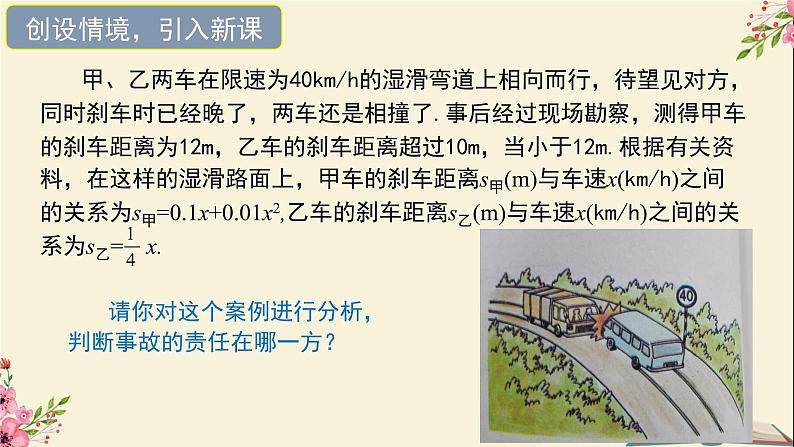
请你对这个案例进行分析，判断事故的责任在哪一方？
根据刹车距离，求出两车的行驶速度，判断是否超速.即由y的值或y的取值范围，求出x的值或x的取值范围.
解：由题意，s甲=0.1x+0.01x2，甲车刹车前的行驶速度 就是当甲车的刹车距离为12m时的车速，即 0.1x+0.01x2=12 解得 x=30或x=－40（舍去） 所以甲车刹车前的行驶速度为30km/h，小于限速值 40km/h 故甲车没有违章超速.
转化为一元二次方程解决问题
乙车刹车前的行驶速度范围为40km/h＜ x＜48km/h，大于限速值40km/h，故乙车违章超速；
转化为一元一次不等式组解决问题
在限速40km/h的前提下，能不能计算出甲车、乙车的刹车距离的范围？从而直接用刹车距离判断两车是否超速？
甲的刹车距离为12m,因此甲没有超速.
乙的刹车距离超过了10m,因此乙超速了.
同样，当二次函数y=ax2+bx+c 的某一个函数值y=m,就可以利用一元二次方程ax2+bx+c=m确定与它对应的x的值.即将二次函数问题转化为一元二次方程问题.
当一次函数y=kx+b的某一个函数值y=m,就可以利用一元一次方程kx+b=m确定与它对应的x的值.即将一次函数问题转化为一元一次方程问题.
1.某商店经销一种销售成本为每千克40元的水产品．据市场分析，若按每千克50元销售，一个月能售出500千克；销售单价每涨1元，月销售量就减少10千克．针对这种水产品的销售情况，商店想在月销售成本不超过10000元的情况下，使得月销售利润达到8000元，销售单价应定为多少？
解：设销售单价为x元/千克，月销售利润为y元.y=(x-40)[500-10(x-50)] =－10x2＋1400x－40000
把y=8000代入，得 －10x2＋1400x－40000=8000 解得 x1＝60，x2＝80．
∵月销售成本不超过10000元
∴40×[500-10（x-50)]≤10000解得，x≥75
答：月销售单价应定为80元/千克.
图中出现了几何中常见的什么基本型？
题中出现“K”形，一般会用到什么知识？
在一元二次方程章节，我们是如何处理“能不能”的问题的？
方程有没有根，即利用根的判别式
解：设BE=x,CE=1-x.
又∵ ∠ABE=∠ECF ,∴ Rt△ABE∽Rt△ECF.
∵∠1+∠3=90°,∠2+∠3=90°∴∠1=∠2.
解：设BE=x,CF=y.
与方法一相同，可证△ABE∽△ECF
∵a=-1＜0,抛物线开口向下
例1 如图，已知边长为1的正方形ABCD,在BC边上有一动点E，连接AE，作EF⊥ AE，交CD边于点F.
1.当二次函数y=ax2+bx+c 的某一个函数值y=m,就得到一元二次方程ax2+bx+c=m.则将二次函数问题转化为一元二次方程问题.就可以用一元二次方程的知识解决问题，如：解方程、根的判别式等等.
2.可以利用相似的知识得到二次函数的表达式.
1.如图，在△ABC中，∠B=90°，AB=12cm,BC=24cm,动点P从点A开始沿边AB向点B以2cm/s的速度移动（不与点B重合），动点Q从点B开始沿边BC向点C以4cm/s的速度移动（不与点C重合）.如果点P、Q同时出发，那么经过几秒，四边形APQC的为112c㎡.
设经过x秒，四边形APQC的面积为112c㎡
∴经过2秒或4秒，四边形APQC的面积为112c㎡.
2.如图，在△ABC中，∠B=90°，AB=12cm,BC=24cm,动点P从点A开始沿边AB向点B以2cm/s的速度移动（不与点B重合），动点Q从点B开始沿边BC向点C以4cm/s的速度移动（不与点C重合）.如果点P、Q同时出发，那么经过几秒，四边形APQC的面积最小.
设经过x秒，四边形APQC的面积为yc㎡
∵a=4＞0,∴当x=3时，y有最小值.
∴经过3秒，四边形APQC的面积最小.
例2 如图，△ABC是一块铁皮余料，已知底边BC=160cm,高AD=120cm.在铁皮余料上截取一个矩形EFGH,使H在AD上，点G在AC上，点E、F在BC上，AD交HG于点M.
（2）用函数解决最值时，首先要解决什么问题？
利用函数解决最值的问题.
求矩形EFGH的最大值.
（1）通常我们会怎样解决“最大”的问题？
（3）在本题中，需要确定什么样的函数表达式？
以矩形边长为自变量，面积为函数的表达式.
解：设HG为xcm,矩形EFGH的面积为yc㎡.
由题得，HG∥BC∴△AHG∽△ABC
∴当x=60时，y有最大值为4800.
即矩形EFGH的最大值为4800c㎡.
1.求最值往往用函数来解决，求哪个数量的最大或最小值，就需要列出以这个数量为函数的表达式，再用函数的顶点坐标或增减性解决问题.
2.与图形相关的函数问题，往往会和以前的相似知识相联系.
1.一人乘雪橇沿一条直线形的斜坡滑下，滑下的路程sm与下滑的时间满足关系式s=10t+t2，当滑下的路程为200m时，所用的时间为 .
2.一根高2m的标杆直立在水平地面上，某时测得这根标杆的影长为3m，同一时刻测得一幢大楼的影子长x m，设这幢大楼的高度为y m，则y与x之间的关系式为 .当x=24m时，这幢大楼的高度为 .
3.一个滑雪者从85m长的山坡滑下，滑行的距离为S（单位：m）与滑行的时间t（单位：s）的函数关系式是S=1.8t+0.064t2，他通过这段山坡需要多长时间？
解：由题意得，S=85 85 =1.8t+0.064t2 解方程得： t1=25或t2 = －53.125（不合题意，舍去） 所以，他通过这段山坡需要25秒的时间
当已知某个二次函数的函数值y = m,求对应的x 的值的基本方法：1.根据题意先确定这个二次函数的解析式 y = ax 2 + bx + c；2.令 y = m，构成ax 2 + bx + c= m的一元二次方程；3.再解一元二次方程，求出符合题意的x 的值.
如果给出的是函数值y的范围，则二次函数可以转换化成一元二次不等式或一元二次不等式组求解.