人教版八年级下册17.1 勾股定理图片课件ppt

这是一份人教版八年级下册17.1 勾股定理图片课件ppt，共23页。
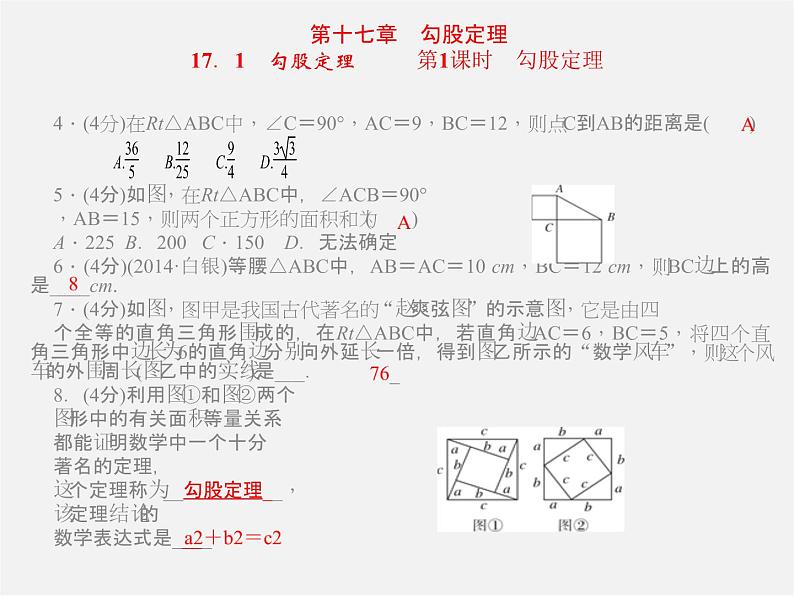
第十七章　勾股定理 17．1　勾股定理 第1课时　勾股定理
4．(4分)在Rt△ABC中，∠C＝90°，AC＝9，BC＝12，则点C到AB的距离是(　　) 5．(4分)如图，在Rt△ABC中，∠ACB＝90°，AB＝15，则两个正方形的面积和为(　　)A．225 B．200 C．150 D．无法确定6．(4分)(2014·白银)等腰△ABC中，AB＝AC＝10 cm，BC＝12 cm，则BC边上的高是____cm.7．(4分)如图，图甲是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，在Rt△ABC中，若直角边AC＝6，BC＝5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图乙所示的“数学风车”，则这个风车的外围周长(图乙中的实线)是___．8．(4分)利用图①和图②两个图形中的有关面积等量关系都能证明数学中一个十分著名的定理，这个定理称为__勾股定理__，该定理结论的数学表达式是____
11．如图所示，以Rt△ABC的三条边为直径分别向外作半圆，设以BC为直径的半圆的面积记作S1，以AC为直径的半圆的面积记作S2，以AB为直径的半圆的面积记作S3，则S1，S2，S3之间的关系正确的是(　　)A．S1＋S2>S3 B．S1＋S2＜S3 C．S1＋ S2＝S3 D．无法确定
12．(2014·凉山)已知一个直角三角形的两边的长分别是3和4，则第三边长为 13．如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7 cm，则正方形A，B，C，D的面积和是__49_cm2__．三、解答题(共40分)14．(8分)如图，Rt△ABC中，∠C＝90°，AD平分∠CAB，DE⊥AB于E，若AC＝6，BC＝8，CD＝3.(1)求DE的长；(2)求△ADB的面积．
15．(8分)如图，Rt△ABC中，∠C＝90°，a，b，c分别是∠A，∠B，∠C的对边长，且a＋b＝7，c＝5，求Rt△ABC的面积．  16．(12分)如图所示，四边形ABCD是长方形，把△ACD沿AC折叠到△ACD′，AD′与BC交于E，若AD＝4，DC＝3，求BE.
【综合应用】17．(12分)如图，公路MN上有一拖拉机由点P向点N行驶，在公路一侧点A处有一所中学，已知PA＝160 m，且∠NPA＝30°.假设拖拉机在行驶时，周围100 m以内会受到噪音影响，那么拖拉机在公路MN上沿PN方向行驶时，学校是否会受到噪音影响？请说明理由．如果受影响，已知拖拉机的速度为18 km/h，那么学校受影响的时间是多少秒？
第2课时　勾股定理的应用
2．(4分)某楼梯的侧面视图如图所示，其中AB＝4米，∠BAC＝30°，∠C＝90°，因某种活动要求铺设红色地毯，则在AB段楼梯所铺地毯的长度应为 (2＋2)米__．3．(4分)如图所示，是一个外轮廓为矩形的机器零件平面示意图，根据图中标出的尺寸(单位：mm)计算两圆孔中心A和B的距离为__100_mm__．
4．(4分)如图，有一块边长为12米的正方形绿地，在绿地旁边B处有健身器材，由于居住在A处的居民去健身时践踏绿地，于是小明在A处立一个标牌“少走_ _步，踏之何忍！”请你在标牌上填上数字．(假设2步为1米) 　  5．(4分)如图，一艘轮船以16海里/时的速度从港口A向东南方向航行，另一艘轮船以12海里/时的速度从港口A同时出发向东北方向航行，则半小时后两船相距__ __海里．6．(4分)如图，有两棵树，一棵高12米，另一棵高6米，两树相距8米，一只鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行__ __米．7．(4分)如图，矩形ABCD边AD沿折痕AE折叠，使点D落在BC上的点F处，已知AB＝6，△ABF的面积是24，则FC等于(　　)A．1　　　　B．2　　　　C．3　　　　D．4
8．(4分)如图是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是(　　)A．12≤a≤13 B．12≤a≤15 C．5≤a≤12 D．5≤a≤139．(8分)如图，在一棵树的10 m高的B处有两只猴子，其中一只猴子爬下树，走到离树20 m处的池塘A处，另一只猴子爬到树顶D后直接跃向池塘A处(假设它经过的路线为直线)，如果两只猴子所经过的路程相等，求这棵树的高．解：设BD＝x m，由题意知BC＋AC＝BD＋AD，∴AD＝(30－x)m，∴(10＋x)2＋202＝(30－x)2，解得x＝5，∴x＋10＝15，即这棵树高15 m
10．如图，每个小正方形的边长为1，△ABC的三边长a，b，c的大小关系是(　　)A．a＜c＜b B．a＜b＜c C．c＜a＜b D．c＜b＜a 　　　　　   11．如图，在四边形ABCD中，∠BAD＝90°，∠CBD＝90°，AB＝3，AD＝4，BC＝12，则正方形DCEF的面积为12．某市在旧城改造中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境，已知这种草皮每平方米售价a元，则购买这种草皮至少需要____元． 13．如图，以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1，再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1……如此作下去，若OA＝OB＝1，则第n个等腰直角三角形的面积Sn＝
14．(2014·潍坊)我国古代有这样一道数学问题：“枯木一根直立地上，高二丈周三尺，有葛藤自根缠绕而上，五周而达其顶，问葛藤之长几何？”题意是：如图，把枯木看作一个圆柱体，因一丈是十尺，则该圆柱的高为20尺，底面周长为3尺，有葛藤自点A处缠绕而上，绕五周后其末端恰好到达点B处，则问题中葛藤的最短长度是____尺． 15．(8分)如图，牧童在A处放牛，牧童家在B处，A，B处相距河岸的距离AC，BD分别为500 m和300 m，且C，D两处的距离为600 m，天黑前牧童从A处将牛牵到河边去饮水，再赶回家，那么牧童最少要走多少米？解：如图，作B关于CD的对称点B′，连AB′，交CD于点P，过A作B′B的垂线，垂足为E，在Rt△AB′E中，AE＝600，B′E＝800，AB′＝1000(米)
16．(10分)一架长5米的梯子AB，斜靠在一竖直墙AC上，这时梯足B到墙底端C的距离为1.4米．(1)此时梯子顶端A距离地面多高？(2)若梯子的顶端沿墙下滑0.8米，那么梯足B是否也外移了0.8米？解：(1)AB2－BC2＝AC2，∴AC2＝52－1.42，AC＝4.8米　 (2)DE＝5，EC＝4，∴DC2＝DE2－EC2＝9，∴DC＝3，∴DC－BC＝3－1.4＝1.6米，∴梯足B向外移动了1.6【综合应用】17．(12分)(2014·牡丹江改编)如图，在等腰△ABC中，AB＝AC，BC边上的高AD＝6 cm，腰AB上的高CE＝8 cm，求：△ABC的周长． 
17．2　勾股定理的逆定理 第1课时　勾股定理的逆定理
1．(3分)(2014·滨州)下列四组线段中，可以构成直角三角形的是(　　)A．4，5，6　　B．1.5，2，2.5 C．2，3，4 D．1，，32．(3分)已知△ABC的三边长分别为5，13，12，则△ABC的面积为(　　)A．30 B．60 C．78 D．不能确定3．(3分)若三角形的三边长分别为n＋1，n＋2，n＋3，如果这个三角形是直角三角形，那么n的值为(　B　)A．1 B．2 C．3 D．不能确定4．(3分)若△ABC的三边a，b，c满足下列关系式|a＋2b－60|＋(b－18)2＋ ＝0，则△ABC为(　A　)A．直角三角形 B．等腰三角形 C．等腰直角三角形 D．无法确定5．(4分)三角形的三边长满足(a＋b)2＝c2＋2ab，则这个三角形是__
6．(6分)在△ABC中，∠A，∠B，∠C的对边分别是a，b，c，根据下列各边的长度，判断各三角形是否为直角三角形．并指出哪一个角是直角． 解：(1)是，∠B是直角　(2)不是　(3)是，∠A是直角    7．(8分)一种机器零件的形状如图所示，按规定这个零件中∠A和∠DBC都应为直角，工人师傅量得这个零件各边尺寸如图所示，这个零件符合要求吗？请说明理由．解：符合要求，理由是：∵152＝225，122＋92＝144＋81＝225，∴152＝122＋92，∴∠A＝90°，同样172＝152＋82，∴∠DBC＝90°，故符合要求      8．(3分)“全等三角形的面积相等”的逆命题是__面积相等的两个三角形全等__，它是__假__(填“真”或“假”)命题．9．(3分)下列说法正确的是(　　)A．每个命题都有逆命 B．真命题的逆命题是真命题C．假命题的逆命题是假命题 D．每个定理都有逆定理10．(4分)下列命题的逆命题正确的是(　　)A．角平分线上的点到这个角两边的距离相等 B．若两个实数相等，则它们的绝对值相等C．全等三角形的对应角相等 D．若两个实数相等，则它们的平方也相等
11．下列各组数据中，是勾股数的为(　　)A．70，240，250 B．79，150，170 12．下列定理中，没有逆定理的是(　　)A．内错角相等，两直线平行 B．直角三角形的两个锐角互余C．对顶角相等 D．两直线平行，同位角相等13．在△ABC中，∠A，∠B，∠C的对边分别是a，b，c，下列说法中，不能推出△ABC是直角三角形的是(　　)A．a2－c2＝b2 B．(a－b)(a＋b)＋c2＝0 C．∠A＝∠B＝∠C D．∠A＝2∠B＝2∠C 14．木工师傅做一个长方形桌面，量得它的长为80分米，宽为60分米，对角线为100分米，则这个桌面_ __．(填“合格”或“不合格”)15．“同角的补角相等”的逆命题是 __，逆命题是__假__(填“真”或“假”)命题．16．已知a，b，c是△ABC三边的长，且满足关系式＋|a－b|＝0，则△ABC的形状为__等腰直角三角形__ 17．(8分)如图，已知在四边形ABCD中，∠B＝90°，AB＝3，BC＝4，CD＝12，AD＝13.求四边形ABCD的面积．
18．(9分)阅读下列解题过程：已知a，b，c为△ABC的三边，且满足a2c2－b2c2＝a4－b4，试判断△ABC的形状．解：∵a2c2－b2c2＝a4－b4①∴c2(a2－b2)＝(a2＋b2)(a2－b2)②∴c2＝a2＋b2.③∴△ABC为直角三角形．(1)上述解题过程，从哪一步开始出现错误？请写出该步的代号__③__；(2)错误的原因是__等号两边不能同时除以a2－b2，因为它有可能为零__；(3)本题正确的结论是__△ABC是直角三角形或等腰三角形__．19．(9分)如图，E，F分别是正方形ABCD中BC和CD边上的点，且AB＝4， F为CD的中点，连接AF，AE，问△AEF是什么三角形？请说明理由．解：△AEF为直角三角形　理由：由勾股定理可得AE2＝25，EF2＝5，AF2＝20，∴AE2＝AF2＋EF2，∴△AEF为直角三角形
【综合应用】20．(10分)张老师在一次“探究性学习”课中，设计了如下数表：(1)请你分别探究a，b，c与n之间的关系，并且用含n(n>1)的式子表示：a＝__n2－1__，b＝__2n__，c＝__n2＋1__．(2)猜想以a，b，c为边的三角形是否为直角三角形？并证明你的猜想．解：(2)是直角三角形，证明：∵a2＋b2＝(n2－1)2＋(2n)2＝n4＋2n2＋1，c2＝(n2＋1)2＝n4＋2n2＋1，∴a2＋b2＝c2，∴以a，b，c为边长的三角形是直角三角形
第2课时　勾股定理及其逆定理的综合应用
1．(3分)如图，小林想检验自己刚加工的门框中每个角是否都为直角，他用直尺量得BE＝30 cm，BF＝40 cm，EF＝50 cm，他认为∠B是直角，其他三个角的检验方法同上，小林验证的根据是__
3．(3分)若一个三角形的三边之比为5∶12∶13，且周长为60 cm，则它的面积为____．4．(3分)为了求出湖两岸的A，B两点之间的距离，一个观测者在点C设桩，使三角形ABC恰好为直角三角形，如图，通过测量，得到AC长160 m，BC长128 m，则从点A穿过湖到点B的距离是(　　) A．48 m B．90 m C．96 m D．69 m
5．(4分)如图，长方体的长为15，宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是(　　) 　　  6．(4分)如图，正方形网格中的△ABC，若小方格边长为1，则△ABC是(　　)A．直角三角形 B．锐角三角形 C．钝角三角形 D．以上答案都不对7．(4分)五根小木棒，其长度分别为7，15，20，24，25，现将它们摆成两个直角三角形，其中正确的是(　　)8．(4分)在△ABC中，D是BC上一点，且BD＝5，AB＝13，AD＝12，AC＝15，则△ABC的面积为(　　) A．30 B．42 C．84 D．100
9．(4分)(2014·安徽)如图，Rt△ABC中，AB＝9，BC＝6，∠B＝90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为(　　) 10．(8分)如图，在C港有甲、乙两艘渔船，若甲船沿北偏东60°方向以每小时8海里速度前进，乙船沿南偏东某方向以每小时15海里速度前进，1小时后甲船到达B岛，乙船到达A岛，且A岛与B岛相距17海里，你能知道乙船沿哪个方向航行吗？解：南偏东30°方向
11．如图，每个小正方形边长为1，A，B，C是小正方形的顶点，则∠ABC的度数为(　　) A．90° B．60° C．45° D．30° 　　　　  12．如图，在由单位正方形组成的网格图中标有AB，CD，EF，GH四条线段，其中能构成一个直角三角形三边的线段是(　　)A．CD，EF，GH B．AB，EF，GH C．AB，CD，GH D．AB，CD，EF
14．如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形，若斜边AB＝3，则图中阴影部分的面积为 　  15．在直线l上依次摆放着五个正方形，如图所示，已知倾斜放置的两个正方形的面积分别是3，5，正放置的三个正方形的面积依次是S1，S2，S3，则S1＋2S2＋S3＝__16．(8分)如图是一个零件的示意图，测量AB＝4厘米，BC＝3厘米，CD＝12厘米，AD＝13厘米，∠ABC＝90°，根据这些条件，你能求出∠ACD的度数吗？试说明理由．解：在△ABC中，∵AB＝4，BC＝3，∠ABC＝90°，∴AC2＝32＋42＝52，∴AC＝5，在△ACD中，CD＝12，AD＝13，AC＝5，即有AC2＋CD2＝AD2，∴∠ACD＝90°