2020-2021学年17.1 勾股定理多媒体教学课件ppt

这是一份2020-2021学年17.1 勾股定理多媒体教学课件ppt，共35页。PPT课件主要包含了学习目标，看一看，a2+b2c2，感悟与反思，a2c2-b2，b2c2-a2，c2a2+b2，b8c10，课堂反馈等内容，欢迎下载使用。

  星期日老师带领初二全体学生去凌峰山风景区游玩,同学们看到山势险峻,查看景区示意图得知:凌峰山主峰高约为900米,如图:为了方便游人,此景区从主峰A处向地面B处架了一条缆车线路,已知山底端C处与地面B处相距1200米, ,请问缆车路线AB长应为多少？
1．了解勾股定理的发现过程，掌握勾股定理的内容，会用面积法证明勾股定理。2．培养在实际生活中发现问题总结规律的意识和能力。3．介绍我国古代在勾股定理研究方面所取得的成就，激发爱国热情，勤奋学习。重点：勾股定理的内容及证明。难点：勾股定理的证明。
（一）、课前准备（2分钟）
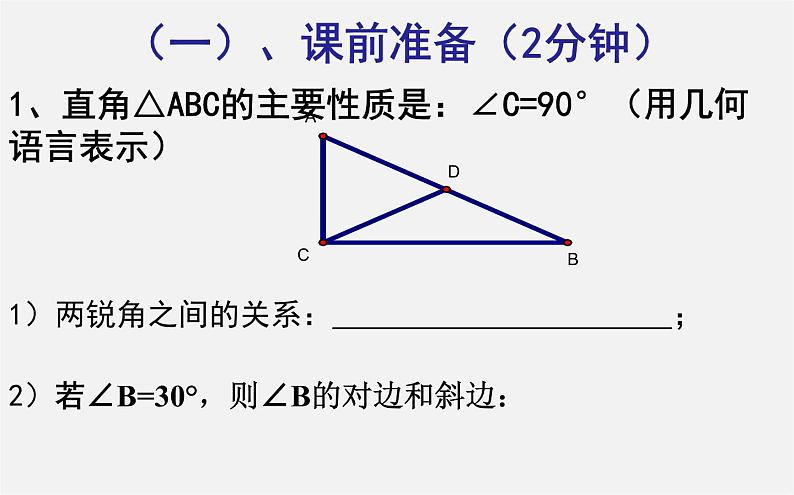
1、直角△ABC的主要性质是：∠C=90°（用几何语言表示）
1）两锐角之间的关系： ；
2）若∠B=30°，则∠B的对边和斜边：
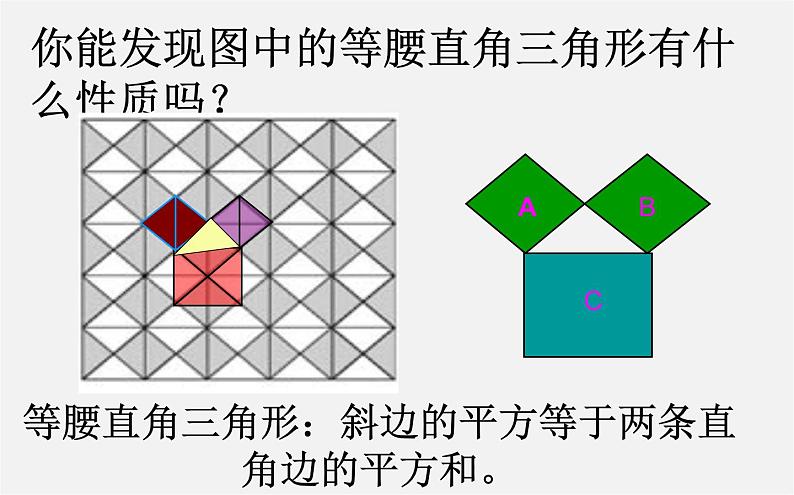
相传两千五百年前，一次毕达哥拉斯去朋友家作客，发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系，同学们，我们也来观察一下图案，看看你能发现什么？
你能发现图中的等腰直角三角形有什么性质吗？
在等腰直角三角形中斜边的平方等于两条直角边的平方和，其他的直角三角形中也有这个性质吗？
一般的直角三角形三边关系
（二）总结规律，大胆才猜想（5分钟）
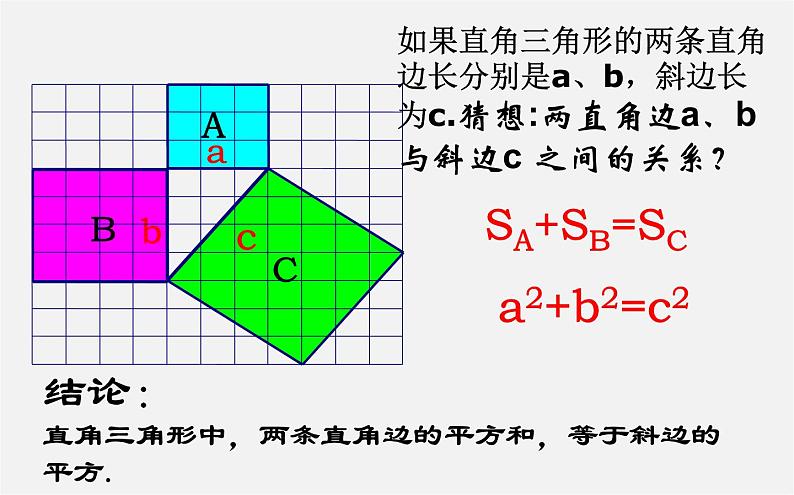
如果直角三角形的两条直角边长分别是a、b，斜边长为c.猜想:两直角边a、b与斜边c 之间的关系？
结论：直角三角形中，两条直角边的平方和，等于斜边的平方.
如果直角三角形两直角边分别为a，b，斜边为c，那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
∵ ∠C＝90° ∴ a2 + b2 = c2
读一读 我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦.图1-1称为“弦图”，最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.图1-2是在北京召开的2002年国际数学家大会（TCM－2002）的会标，其图案正是“弦图”，它标志着中国古代的数学成就.　　　　　　　
∵ ab×4+(b-a)²=c²
2ab+（b²-2ab+a²）=c²
【证法1】（赵爽证明）
S=1/2ab×4+ c²=1/2ab ×4+ a²+b² a²+b² =c²
【证法2】已知：在△ABC中，∠C=90°，∠A、∠B、∠C的对边为a、b、c。求证：a2＋b2=c2
【 证法3】（1876年美国总统Garfield证明）
以a、b 为直角边，以c为斜边作两个全等的直角三角形，则每个直角三角形的面积等于ab. 把这两个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上.
∵S梯形ABCD=1/2(a+b)(a+b) =1/2ab×2+1/2 c²
分析：已知△ABC中，
，                                        AC=900米，BC=1200米，          求斜边AB的长.
 例：星期日老师带领初二全体学生去凌峰山风景区游玩,同学们看到山势险峻,查看景区示意图得知:凌峰山主峰高约为900米,如图:为了方便游人,此景区从主峰A处向地面B处架了一条缆车线路,已知山底端C处与地面B处相距1200米,
,请问缆车路线AB长应为多少?                                                               
三、应用定理 巩固新知
1、如图，直角△ABC的主要性质是：∠C=90°，（用几何语言表示）⑴两锐角之间的关系： ；(2)若∠B=30°，则∠B的对边和斜边： ；(3)三边之间的关系：
1、在Rt△ABC中，∠C=90°①若a=5，b=12，则c=___________；②若a=15，c=25，则b=___________；③若c=61，b=60，则a=__________；④若a∶b=3∶4，c=10则SRt△ABC =________。
2、已知在Rt△ABC中，∠B=90°，a、b、c是△ABC的三边，则⑴c= 。（已知a、b，求c）⑵a= 。（已知b、c，求a）
3、直角三角形两直角边长分别为5和12，则它斜边上的高为__________。4、.已知一个Rt△的两边长分别为3和4，则第三边长的平方是（　　） A、25 B、14C、7D、7或255、等腰三角形底边上的高为8，周长为32，则三角形的面积为（　　） A、56B、48C、40D、32
必做题：课本77页第1、2、3题. 选做题：收集有关勾股定理的其它 证明方法，下节课展示、 交流.
勾股定理的运用已知直角三角形的任意两条边长，求第三条边长.
（三）随堂练习 1、在Rt△ABC中， ，1）如果a=3，b=4，则c=________；2）如果a=6，b=8，则c=________；3）如果a=5，b=12，则c=________；4) 如果a=15，b=20，则c=________.
2、下列说法正确的是（　　）A.若a、b、c是△ABC的三边，则:B.若a、b、c是Rt△ABC的三边，则C.若a、b、c是Rt△ABC的三边， ， 则D.若a、b、c是Rt△ABC的三边， ，则
3、一个直角三角形中，两直角边长分别为3和4，下列说法正确的是（ ）A．斜边长为25 B．三角形周长为25 C．斜边长为5 D．三角形面积为204、如图,三个正方形中,S1＝25，S2＝144，则另一个的面积S3为________． 5、一个直角三角形的两边长分别为5cm和12cm,则第三边的长为 。
在直角三角形ABC中，∠C=900，∠A、∠B、∠C所对的边分别为a、b、c （1）       已知a=1，b=2，求c （2）       已知a=10，c=15，求b
例2：将长为5米的梯子AC斜靠在墙上，BC长为2米，求梯子上端A到墙的底端B的距离.
P的面积 =______________
X=_________
AB=__________
AC=__________
BC=__________
求下列图中表示边的未知数x、y、z的值.
比一比看谁算得又快又准！
求下列直角三角形中未知边的长x:
可用勾股定理建立方程.
1、直角ABC的两直角边a=5,b=12,c=_____ 2、直角ABC的一条直角边a=10,斜边 c=26，则b= ( ).３、已知：∠C＝90°，a=6， a：b＝3：4，求b和c.
１、本节课我们经历了怎样的过程？
　　经历了从实际问题引入数学问题然后发现定理，再到探索定理，最后学会验证定理及应用定理解决实际问题的过程.
　２、本节课我们学到了什么？
　　通过本节课的学习我们不但知道了著名的勾股定理，还知道从特殊到一般的探索方法及借助于图形的面积来探索、验证数学结论的数形结合思想.
３、学了本节课后我们有什么感想？
　　 很多的数学结论存在于平常的生活中，需要我们用数学的眼光去观察、思考、发现，这节课我们还受到了数学文化辉煌历史的教育.
分层测试:
A组: 1、在 中， ， AB=7, AC=3,求BC的长. B组: 2、如图，在矩形ABCD中， DE⊥AC于E，设AE=8， 且AD=10, EC = 4, 求DE 和AB的长