




初中数学人教版九年级上册22.3 实际问题与二次函数图片ppt课件
展开
这是一份初中数学人教版九年级上册22.3 实际问题与二次函数图片ppt课件,共21页。PPT课件主要包含了自主学习指向目标,学习目标,合作探究达成目标,我们来比较一下,针对练一,针对练二,总结梳理内化目标等内容,欢迎下载使用。
创设情境 明确目标
1.会建立恰当的平面直角坐标系,构建二次函数模型,解决抛物线拱桥问题.
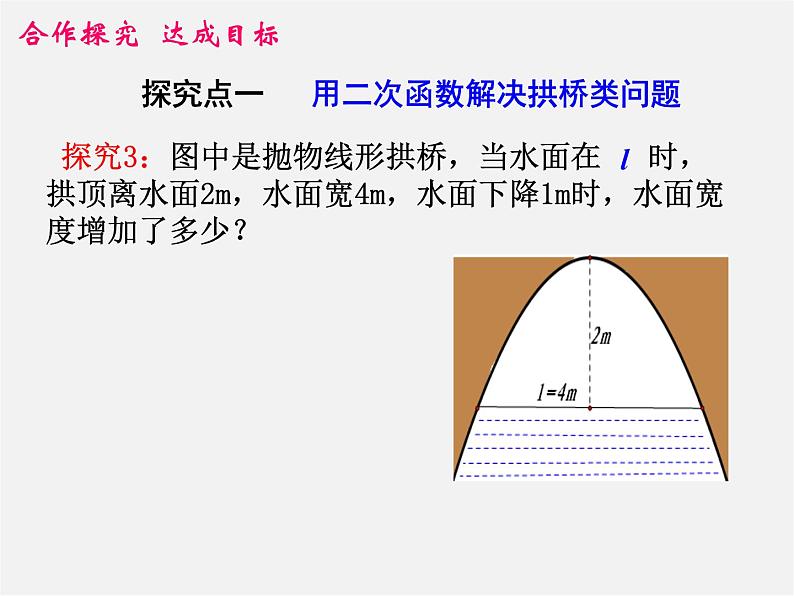
探究点一 用二次函数解决拱桥类问题
探究3:图中是抛物线形拱桥,当水面在 时,拱顶离水面2m,水面宽4m,水面下降1m时,水面宽度增加了多少?
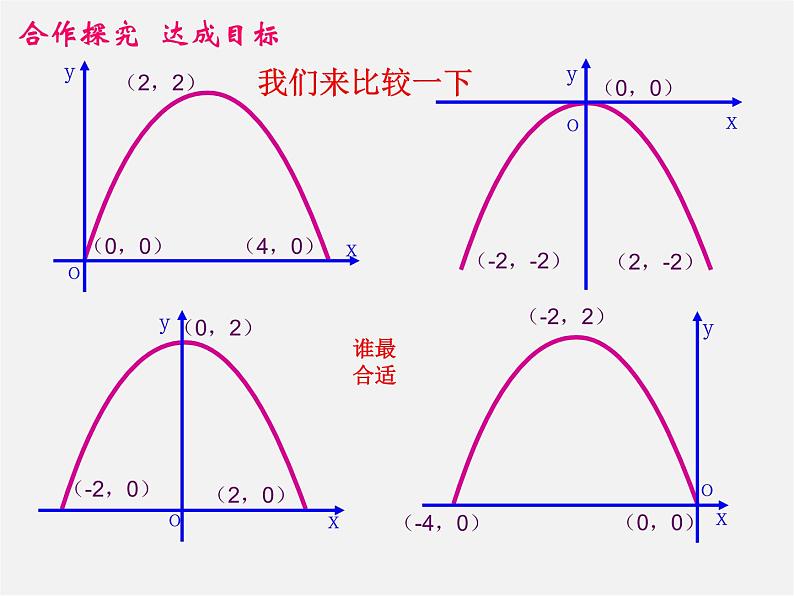
解法一: 如图所示以抛物线的顶点为原点,以抛物线的对称轴为y轴,建立平面直角坐标系.
∴可设这条抛物线所表示的二次函数的解析式为:
当拱桥离水面2m时,水面宽4m
即抛物线过点(2,-2)
∴这条抛物线所表示的二次函数为:
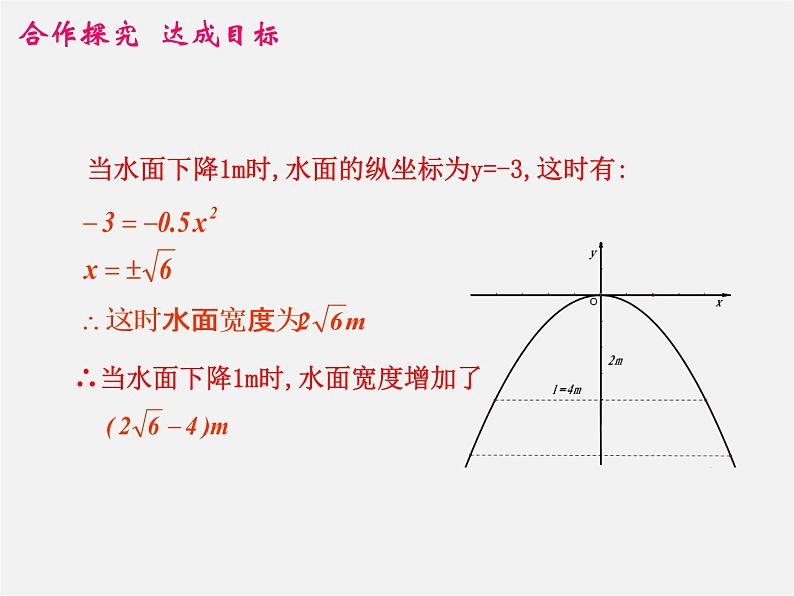
当水面下降1m时,水面的纵坐标为y=-3,这时有:
∴当水面下降1m时,水面宽度增加了
解法二: 如图所示,以抛物线和水面的两个交点的连线为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系.
此时,抛物线的顶点为(0,2)
即:抛物线过点(2,0)
当水面下降1m时,水面的纵坐标为y=-1,这时有:
解法三:如图所示,以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.
∵抛物线过点(0,0)
此时,抛物线的顶点为(2,2)
回顾上一节“最大利润”和本节“桥梁建筑”解决问题的过程,你能总结一下解决此类问题的基本思路吗?与同伴交流.
2.分析问题中的变量和常量,以及它们之间的关系
3.用数学的方式表示出它们之间的关系;
“二次函数应用”的思路
1.某涵洞是抛物线形,它的截面如图所示,现测得水面宽1.6m,涵洞顶点O到水面的距离为2.4m,在图中直角坐标系内,涵洞所在的抛物线的函数关系式是___________.2.在上题中,若水面下降,宽度变为2米,此时水面离涵洞顶点的距离为_______米。
探究点二 用二次函数解决生活中的实际问题
例:飞机着陆后滑行的距离s(单位:m)与滑行的时间t(单位:s)的函数关系式是s=60t-1.5t2 ,飞机着陆后滑行多少秒才能停下来?
思考:飞机从着陆的一瞬间开始计时,到滑行到最远距离停下来所用的时间即为所求,也就是使S取得什么值时的t的值?
解: s=60t-1.5t2 =-1.5(t-20)2+600 ∴当t=20时,s最大,此时飞机才能停下来。
解题步骤:1.分析题意,把实际问题转化为数学问题,画出图形.2.根据已知条件建立适当的平面直角坐标系.3.选用适当的解析式求解.4.根据二次函数的解析式解决具体的实际问题.
3.一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=— 铅球运行路线如图,则他将
铅球推出的水平距离是:_________m.
达标检测 反思目标
上交作业:教科书第42页第11.12题 .










