2020-2021学年25.2 用列举法求概率图片ppt课件

这是一份2020-2021学年25.2 用列举法求概率图片ppt课件，共27页。PPT课件主要包含了整合知识，几何概率PA，课后习题，方法一列表，学科内综合，生活相关问题等内容，欢迎下载使用。
2.同时抛掷两枚质地均匀的硬币，求下列事件的概率：（1）两枚硬币全部正面向上。（2）一枚硬币正面向上，一枚硬币反面向上。
小明的解法如下,他的解答正确吗？解：同时抛掷两枚硬币的全部情况有3种，分别是：正正，反反，反正∴ P(两枚硬币全部正面向上）=P(一枚硬币正面向上，一枚硬币反面向上)=
1.口袋中1红3黑共4个小球，一次从中取出两个小球，求 “取出的小球都是黑球”的概率
解：一次从口袋中取出两个小球时， 所有可能出现的结果共6个，即（红，黑1）（红，黑2）（红，黑3）（黑1，黑2）（黑1，黑3）（黑2，黑3）且它们出现的可能性相等。满足取出的小球都是黑球（记为事件A）的结果有3个，即（黑1，黑2）（黑1，黑3）（黑2，黑3） ， 则 P（A）= =
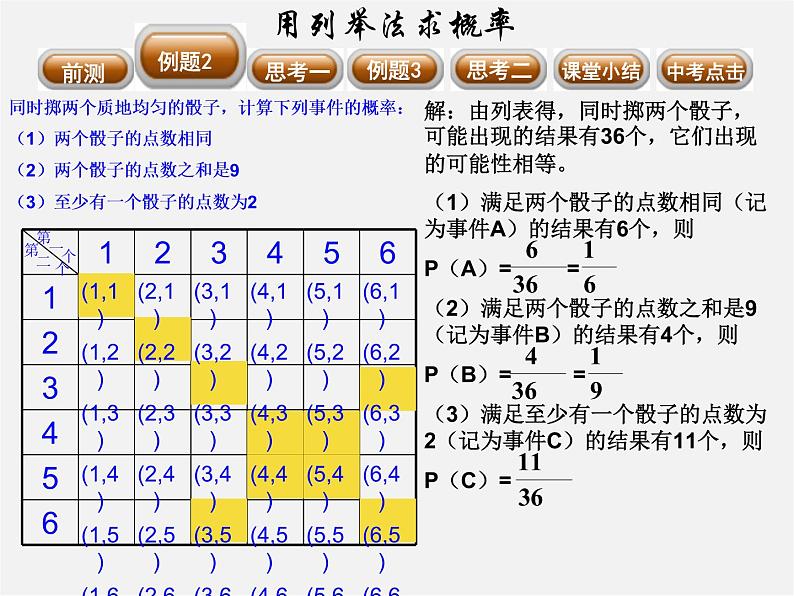
同时掷两个质地均匀的骰子，计算下列事件的概率：（1）两个骰子的点数相同（2）两个骰子的点数之和是9（3）至少有一个骰子的点数为2
同时掷两个质地均匀的骰子，计算下列事件的概率：（1）两个骰子的点数相同（2）两个骰子的点数之和是9（3）至少有一个骰子的点数为2
解：由列表得，同时掷两个骰子，可能出现的结果有36个，它们出现的可能性相等。（1）满足两个骰子的点数相同（记为事件A）的结果有6个，则P（A）= =（2）满足两个骰子的点数之和是9（记为事件B）的结果有4个，则P（B）= =（3）满足至少有一个骰子的点数为2（记为事件C）的结果有11个，则P（C）=
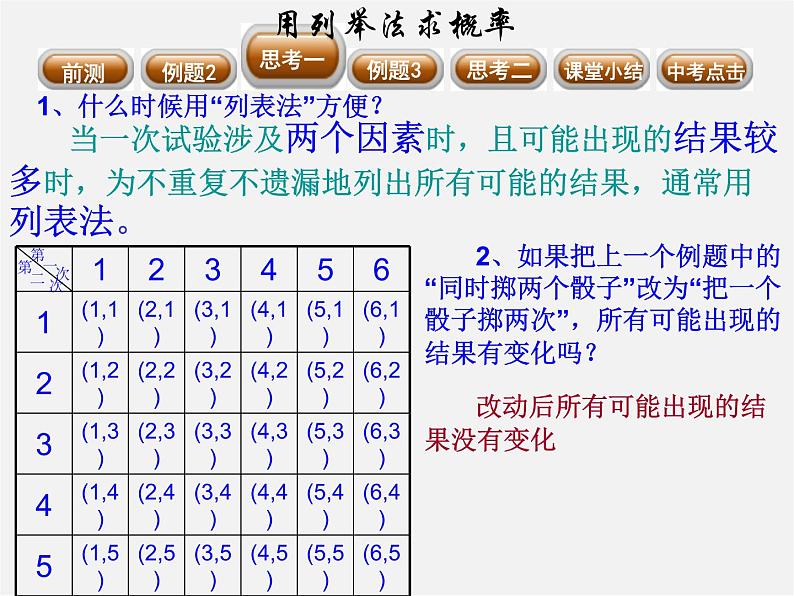
2、如果把上一个例题中的“同时掷两个骰子”改为“把一个骰子掷两次”，所有可能出现的结果有变化吗？
当一次试验涉及两个因素时，且可能出现的结果较多时，为不重复不遗漏地列出所有可能的结果，通常用列表法。
1、什么时候用“列表法”方便？
改动后所有可能出现的结果没有变化
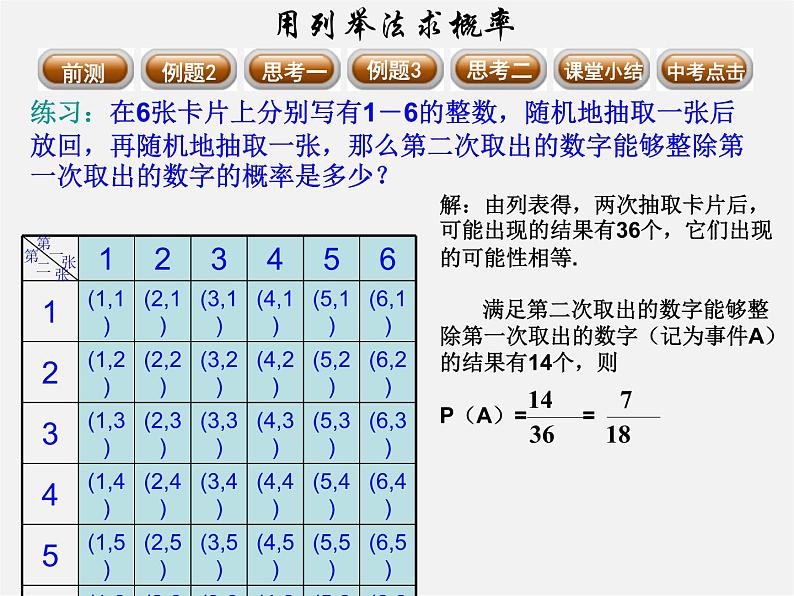
练习：在6张卡片上分别写有1－6的整数，随机地抽取一张后放回，再随机地抽取一张，那么第二次取出的数字能够整除第一次取出的数字的概率是多少？
解：由列表得，两次抽取卡片后，可能出现的结果有36个，它们出现的可能性相等. 满足第二次取出的数字能够整除第一次取出的数字（记为事件A）的结果有14个，则P（A）= =
甲口袋中装有2个相同的小球，它们分别写有字母A和B； 乙口袋中装有3个相同的小球，它们分别写有字母C、D和E；丙口袋中装有2个相同的小球，它们分别写有字母H和I。从3个口袋中各随机地取出1个小球。（1）取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少？（2）取出的3个小球上全是辅音字母的概率是多少？
本题中元音字母: A E I 辅音字母: B C D H
甲口袋中装有2个相同的小球，它们分别写有字母A和B； 乙口袋中装有3个相同的小球，它们分别写有字母C、D和E；丙口袋中装有2个相同的小球，它们分别写有字母H和I。 从3个口袋中各随机地取出1个小球。（1）取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少？ （2）取出的3个小球上全是辅音字母的概率是多少？
解：由树形图得，所有可能出现的结果有12个，它们出现的可能性相等。（1）满足只有一个元音字母的结果有5个，则 P（一个元音）=满足只有两个元音字母的结果有4个，则 P（两个元音）= =满足三个全部为元音字母的结果有1个，则 P（三个元音）=（2）满足全是辅音字母的结果有2个，则 P（三个辅音）= =
想一想，什么时候用“列表法”方便，什么时候用“树形图”方便？
当一次试验涉及两个因素时，且可能出现的结果较多时，为不重复不遗漏地列出所有可能的结果，通常用列表法
当一次试验涉及3个因素或3个以上的因素时，列表法就不方便了，为不重复不遗漏地列出所有可能的结果，通常用树形图
在一个盒子中有质地均匀的3个小球，其中两个小球都涂着红色，另一个小球涂着黑色，则计算以下事件的概率选用哪种方法更方便？1、从盒子中取出一个小球，小球是红球的概率2、从盒子中每次取出一个小球，取出后再放回，取出两球的颜色相同的概率3、从盒子中每次取出一个小球，取出后再放回，连取了三次，三个小球的颜色都相同的概率
求概率的方法有哪些种？应怎样进行选择？
1、当一次试验涉及两个因素时，且可能出现的结果较多时，为不重复不遗漏地列出所有可能的结果，通常用列表法
2、当一次试验涉及3个因素或3个以上的因素时，列表法就不方便了，为不重复不遗漏地列出所有可能的结果，通常用树形图
经过某十字路口的汽车，它可能继续直行，也可能左转或右转，如果这三种可能性大小相同，同向而行的三辆汽车都经过这个十字路口时，求下列事件的概率：（1）三辆车全部继续直行（2）两辆车右转，一辆车左转（3）至少有两辆车左转
解：由树形图得，所有可能出现的结果有27个，它们出现的可能性相等。（1）三辆车全部继续直行的结果有1个，则 P（三辆车全部继续直行）=（2）两辆车右转，一辆车左转的结果有3个，则 P（两辆车右转，一辆车左转）= =（3）至少有两辆车左转的结果有7个，则 P（至少有两辆车左转）=
　　何时用完全列举法，何时用列表法，何时用树形图法比较方便。
　　利用树形图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率.当试验包含一步时,用完全列举法，当试验包含两步时,列表法比较方便,当然,此时也可以用树形图法,当试验在三步或三步以上时,用树形图法方便.
求古典概率的公式P(A)=
将三粒均匀的分别标有1，2，3，4，5，6，的正六面体骰子同时掷出，出现的数字分别为a，b，c，则a，b，c正好是直角三角形三边长的概率是 多少？
1.如图，小明的奶奶家到学校有3条路可走，学校到小明的外婆家也有3条路可走，若小明要从奶奶家经学校到外婆家，不同的走法共有________种2.两道单项选择题都含有A、B、C、D四个选项，若某学生不知道正确答案就瞎猜，则这两道题恰好全部被猜对的概率是（ ） A B C D
3.某校八年级将举行班级乒乓球对抗赛，每个班必须选派出一对男女混合双打选手参赛，八年级一班准备在小娟、小敏、小华三名女选手和小明、小强两名男选手中，选男、女选手各一名组成一对参赛组合，一共能够组成哪几对？如果小敏和小强的组合是最强组合，那么采用随机抽签的办法，恰好选出小敏和小强参赛的概率是多少？
5.“石头、剪刀、布”是个广为流传的游戏，游戏时甲乙双方每次做“石头”、“剪刀”、“布”三种手势中的一种，规定：“石头”胜“剪刀”，“剪刀”胜“布”，“布”胜“石头”，同种手势不分胜负须继续比赛．假定甲乙两人每次都是等可能地做这三种手势，那么一次比赛时两人做同种手势（即不分胜负）的概率是多少？
解：所有可能出下的结果如下：
所有机会均等的结果有9个，
其中的3个做同种手势（即不分胜负）,
1、 如图,有两个可以自由转动的均匀转盘A、B，转盘A被均匀地分成4等份，每份分别标上1、2、3、4四个数字；转盘B被均匀地分成6等份，每份分别标上1、2、3、4、5、6六个数字．有人为甲、乙两人设计了一个游戏，其规则如下： （1）同时自由转动转盘A、B； （2）转盘停止后，指针各指向一个数字（如果指针恰好指在分格线上，那么重转一次，直到指针指向某一数字为止），用所指的两个数字相乘，如果得到的积是偶数，那么甲胜；如果得到的积是奇数，那么乙胜．
你认为这样的规则是否公平？请说明理由；如果不公平，请你设计一个公平的规则，并说明理由．
2.2012年，锦州市被国家评为无偿献血先进城市，医疗临床用血实现了100％来自公民自愿献血，无偿献血总量5.5吨，居全省第三位. 现有三个自愿献血者，两人血型为O型，一人血型为A型.若在三人中随意挑选一人献血，两年以后又从此三人中随意挑选一人献血，试求两次所抽血的血型均为O型的概率. (要求：用列表或画树状图的方法解答)
3、请你依据下图中的寻宝游戏规则，探究“寻宝游戏”的奥秘：⑴用树状图表示出 所有可能的寻宝情况；⑵求在寻宝游戏中胜出 的概率。
4.有两双手套，形状、大小，完全相同，只有颜色不同。黑暗中，任意抽出两只配成一双的概率是多少？
5.点M（x,y） x, y可以在数字－１，０，１，２中任意选取．试求（１）点M在第一象限内的概率．
6.一个家庭有3个孩子(1)求这个家庭有3个男孩的概率;(2)求这个家庭有2个男孩和一个女孩的概率;(3)求这个家庭至少有一个男孩的概率.