初中数学人教版九年级上册第二十三章 旋转23.2 中心对称23.2.1 中心对称教案

这是一份初中数学人教版九年级上册第二十三章 旋转23.2 中心对称23.2.1 中心对称教案，共3页。教案主要包含了重点难点，新课导入，课堂探究等内容，欢迎下载使用。
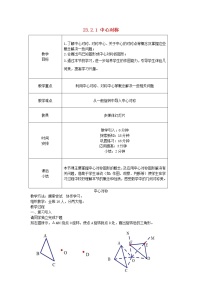
中心对称　　　 　　　　　　　　　　　　　1.了解中心对称、对称中心、关于中心的对称点等概念,并能运用它们解决简单的问题;2.理解并初步应用关于中心对称的两个图形的性质;3.能熟练画出一个图形关于中心对称的图形.【重点难点】中心对称及其性质,并能运用其进行相关的证明与计算.【新课导入】请同学们观察图片(见课件)你有什么发现?【课堂探究】一、两个图形关于中心对称的概念及性质1.关于中心对称的两个图形,对应线段的关系是(　D　)(A)相等且在同一条直线上(B)平行(C)平行且相等(D)相等、平行或在同一条直线上2.如图,△ABO与△CDO关于点O成中心对称,则在一直线上的三点有　A,O,C以及B,O,D　,并且AO=　CO　,BO=　DO　,△ABO与△CDO的关系是　全等　. 二、画出一个图形关于中心对称的图形3.如图:已知线段AB与CD关于点P中心对称,且点A关于P的对称点为点C.请你在下图的正方形方格纸中,(1)找出对称中心P点;(2)画出线段CD.提示:(1)连AC,线段AC中点就是对称中心P;(2)连BP并延长至D点,使DP=BP,连接CD.解:4.如图,已知△ABC和过点O的两条互相垂直的直线x、y,画出△ABC关于直线x对称的△A'B'C',再画出△ABC关于直线y对称的△A″B″C″,则△A″B″C″与△A'B'C'是否关于点O成中心对称?解:是.1.中心对称的性质(1)中心对称的两个图形,对称点所连线段都经过　对称中心　,而且被　对称中心　所平分. (2)中心对称的两个图形是　全等图形　. 2.中心对称的作图(1)定关键点:确定已知图形的关键点;(2)找对称点:找关键点的中心对称点;(3)连线成图:顺次连接对称点所得中心对称图形. 1.下列说法不正确的是(　D　)(A)关于中心对称的两个图形面积相等(B)关于中心对称的两个图形周长相等(C)关于中心对称的对称点连线经过对称中心(D)关于中心对称的两个图形一定关于直线对称2.如图所示的四组图形中,左边图形与右边图形成中心对称的有(　C　)(A)1组 (B)2组 (C)3组 (D)4组3.请在这一组图形符号中找出它们所蕴含的内在规律,然后在横线的空白处设计一个恰当的图形.答案:4.(2013邵阳)如图所示,将△ABC绕AC的中点O顺时针旋转180°得到△CDA,添加一个条件　∠B=90°　,使四边形ABCD为矩形. 5.如图,已知▱ABCD的对角线BD=4 cm,将▱ABCD绕其对称中心O旋转180°,则点D所转过的路径长为　2π cm　.