数学九年级上册22.3 实际问题与二次函数第2课时教学设计及反思

教

学

目

标

知识

技能

1.通过探究掌握利用二次函数的知识分析解决有关面积问题的实际问题.

2.通过探究掌握利用图形之间的关系列出函数解析式

过程

方法

1.培养学生建模思想.

2.通过图形间的关系，进一步体会函数，体验运动变化的思想.

情感

态度

通过练习让学生体会数学在生活中的应用，培养学生的数学学习兴趣.

重点

用二次函数的知识分析解决有关面积问题的实际问题.

难点

通过图形之间的关系列出函数解析式.

环节

教学问题设计

教学活动设计

情

境

引

入

创设情景  引入新课

1.正方体的六个面是全等的正方形，设正方形的棱长为x，表面积为y，求y与x之间的函数关系式，并求出自变量x的取值范围

2.一个圆柱的高等于底面半径，写出它的表面积S与半径r之间的函数关系式

3.一个长方形的长是宽的2倍，写出长方形的面积与宽之间的函数关系式

4.已知一个矩形的周长为12米，设矩形的一边长为xm，面积为Sm2，求S与x之间的函数关系式，并确定自变量的取值范围

首先让学生明确矩形、圆、三角形、正方体、圆柱的面积以及表面积公式.

思考解答写出关系式.

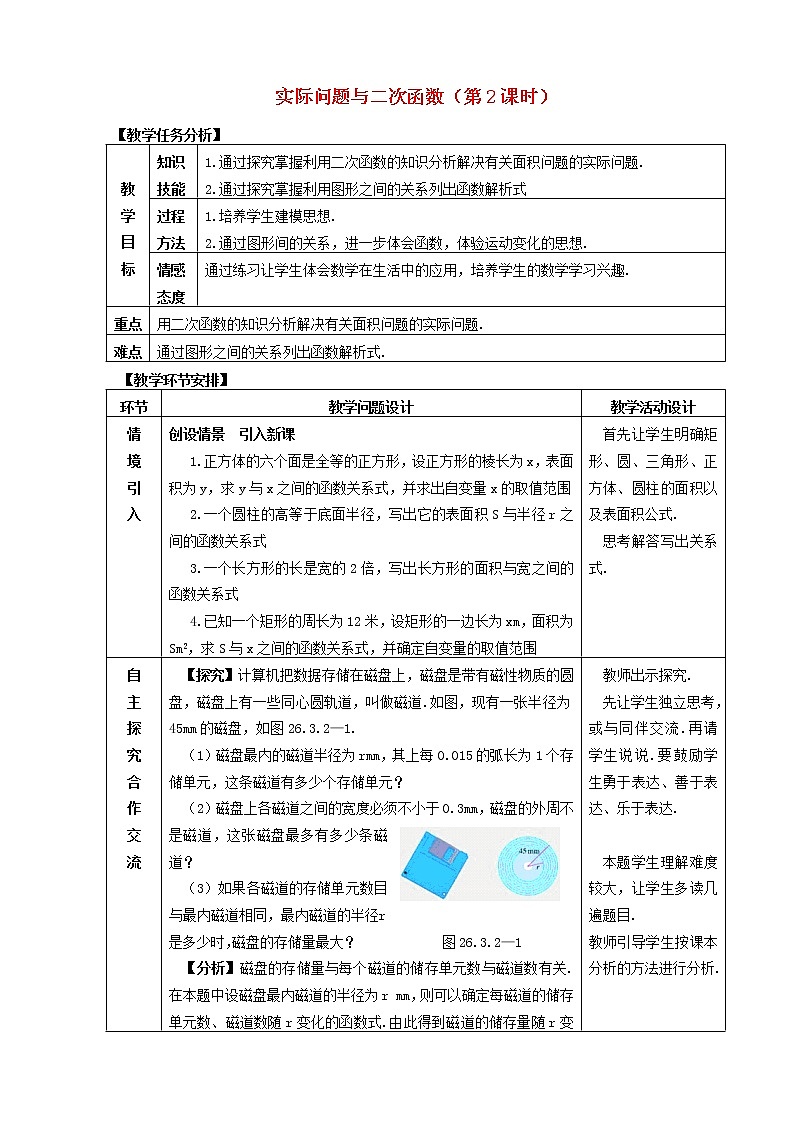
自

主

探

究

合

作

交

流

【探究】计算机把数据存储在磁盘上，磁盘是带有磁性物质的圆盘，磁盘上有一些同心圆轨道，叫做磁道.如图，现有一张半径为45mm的磁盘，如图26.3.2—1.

（1）磁盘最内的磁道半径为rmm，其上每0.015的弧长为1个存储单元，这条磁道有多少个存储单元？

（2）磁盘上各磁道之间的宽度必须不小于0.3mm，磁盘的外周不是磁道，这张磁盘最多有多少条磁道？

（3）如果各磁道的存储单元数目与最内磁道相同，最内磁道的半径r是多少时，磁盘的存储量最大？            图26.3.2—1

【分析】磁盘的存储量与每个磁道的储存单元数与磁道数有关.在本题中设磁盘最内磁道的半径为r mm，则可以确定每磁道的储存单元数、磁道数随r变化的函数式.由此得到磁道的储存量随r变化的函数式，由这个函数求出最大储藏量由学生完成.

教师出示探究.

先让学生独立思考，或与同伴交流.再请学生说说.要鼓励学生勇于表达、善于表达、乐于表达.

本题学生理解难度较大，让学生多读几遍题目.

教师引导学生按课本分析的方法进行分析.

尝

试

应

用

【例题】 1．一块三角形废料如图26.3.2—2所示，∠A＝30°，∠C＝90°，AB＝12.用这块废料剪出一个长方形CDEF，其中，点D、E、F分别在AC，AB，BC上，要使剪出的长方形CDEF面积最大，点E应选在何处？

图26.3.2—2

【分析】师生共同分析：长方形CDEF面积是大三角形的面积减去两个小三角形的面积.

解：（略）

教师出示例题.

请一位学生板练，其他学生练习.完成练习后，先在小组内进行交流、讨论.

成果

展示

用一段长30m的篱笆，围城一个一边靠墙的矩形菜园，墙长为18m.，如图26.3.2—3所示，这个矩形的长、宽为多少时，菜园的面积最大，最大面积为多少？

1.抓住图形的特点进行建模

2.注意实际问题的自变量的取值范围

补

偿

提

高

1.如图26.3.2—5，点E、F、G、H分别位于正方形ABCD的四边上.四边形EFGH也是正方形.当点E位于何处时，正方形EFGH的面积最小？

图26.3.2—4                 图26.3.2—5

2.如图，在△ABC中，∠B＝90°，AB＝12，BC＝24，动点P从A开始沿边AB向B以2的速度移动，动点Q从B开始沿边BC以4的速度移动，如果P、Q分别从A、B同时出发，那么△PBQ的面积随S出发时间如何变化？写出函数关系式及t的取值范围.

针对前几个环节出现的问题，进行针对性的补偿，对学有余力的学生拓展提高.

作业

设计

作业：1.必做：课本第52页，4、5题.

作业设必做题