冀教版九年级下册29.5 正多边形与圆优质ppt课件

这是一份冀教版九年级下册29.5 正多边形与圆优质ppt课件，共26页。PPT课件主要包含了学习目标，新课学习，正多边形的概念，正多边形，各边相等，各角相等，缺一不可，不是中心对称图形，中心对称图形，正三角形等内容，欢迎下载使用。

1.了解正多边形和圆的有关概念.2.理解并掌握正多边形半径、中心角、边心距、边 长之间的关系. 3.会应用正多边形和圆的有关知识解决实际问题.
创设问题情境，引入新课
从以上图片中，你发现了什么样的多边形？我们身边有许多多边形，它们会有哪些性质呢？今天我们就来共同学习一下吧
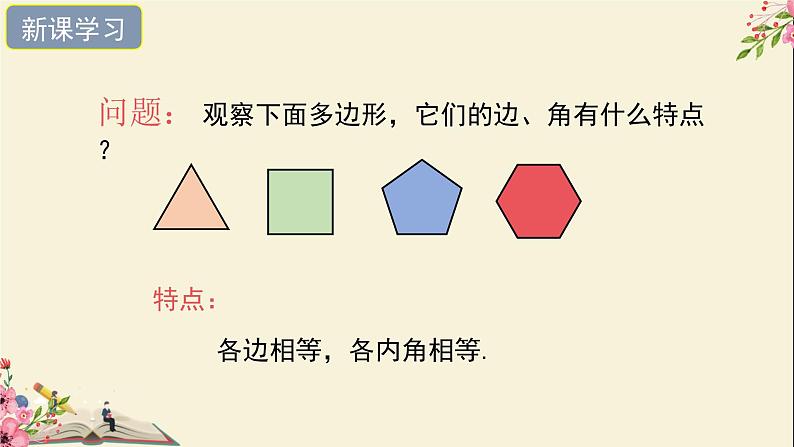
问题： 观察下面多边形，它们的边、角有什么特点？
各边相等，各内角相等.
各边相等,各角也相等的多边形叫做正多边形.
思考： 矩形是正多边形吗？为什么？菱形是正多边形吗？为什么？
矩形不是正多边形，因为矩形不符合“各边相等”.
菱形不是正多边形，因为菱形不符合“各角相等”.
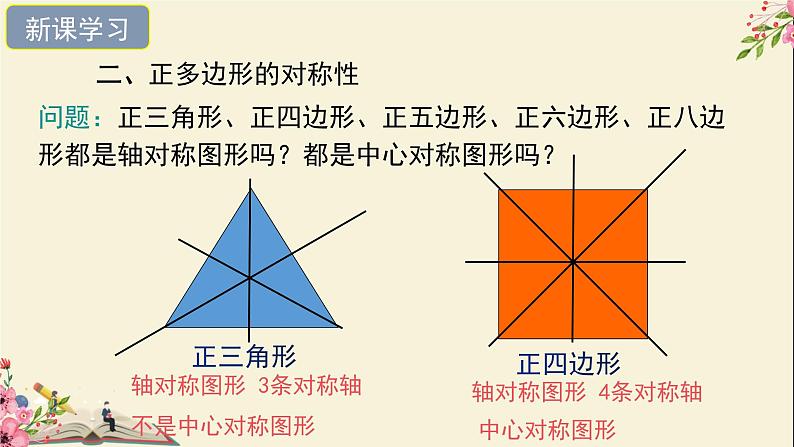
问题：正三角形、正四边形、正五边形、正六边形、正八边形都是轴对称图形吗？都是中心对称图形吗？
二、正多边形的对称性
轴对称图形 3条对称轴
轴对称图形 4条对称轴
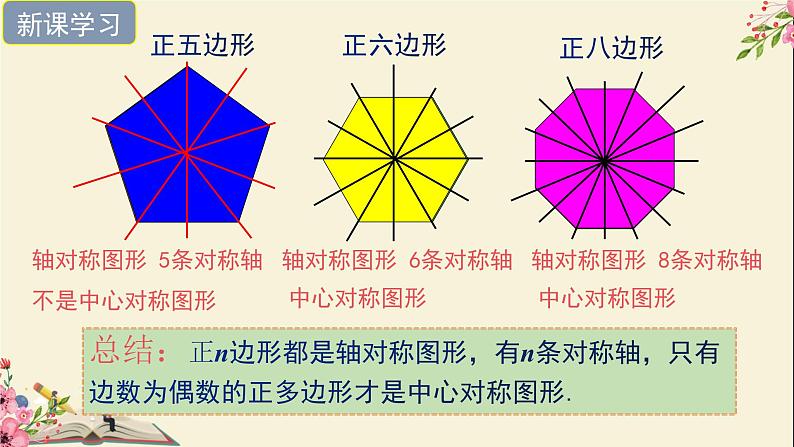
总结：正n边形都是轴对称图形，有n条对称轴，只有边数为偶数的正多边形才是中心对称图形.
轴对称图形 5条对称轴
轴对称图形 6条对称轴
轴对称图形 8条对称轴
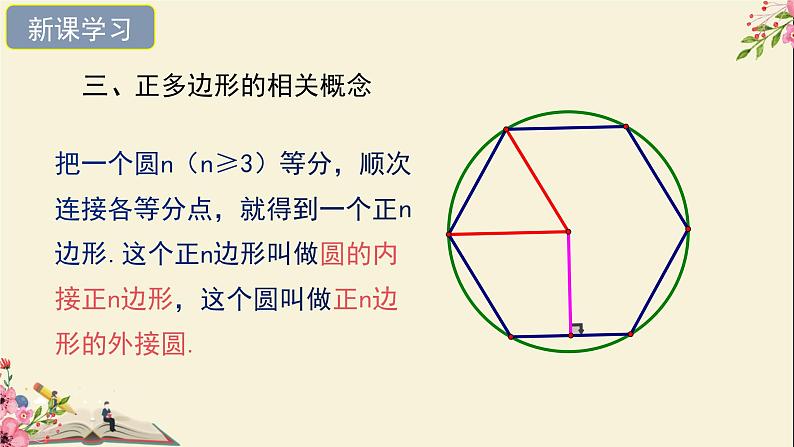
三、正多边形的相关概念
把一个圆n（n≥3）等分，顺次连接各等分点，就得到一个正n边形.这个正n边形叫做圆的内接正n边形，这个圆叫做正n边形的外接圆.
1.外接圆的圆心叫做正多边形的中心.图中点O.
2.外接圆的半径叫做正多边形的半径.图中OA.
3.每一边所对的圆心角叫做正多边形的中心角.图中∠AOF.
4.中心到边的距离叫做正多边形的边心距.图中OM.
四、正多边形和圆的关系
五、正多边形的有关结论
半径、边心距、边的一半
1.如图，AC是⊙O的内接六边形的一边，点B在弧AC上，且BC是⊙O的内接正十边形的一边，若AB是⊙O的内接正n边形的一边，则n=____.
例1.（课本17页例1）用尺规作圆的内接正方形.
作法：1.作直径AB.2.作与AB垂直的直径CD.3.顺次连接AC,CB,BD,DA.四边形ACBD即为所求.
已知：⊙O.求作：正方形ACBD内接于⊙O.
分析：正方形的中心角是90°，作两条互相垂直的直径即可.
证明：∵AB⊥CD∴∠AOC=∠COB=∠BOD=∠DOAAC=CB=BD=DA∵AB,CD是直径∴∠DAC=∠ACB=∠CBD=∠BDA=90°∴四边形ABCD是正方形.
思考一：如何用尺规作正八边形？（在练习本上画出）
作互相垂直的直径，做直径夹角的平分线，出现45°的中心角，进而确定圆的八等分点，依次连接.
思考二：如何用尺规作正六边形？（在练习本上画出）
作半径为边的等边三角形，出现60°的中心角.可确定圆的六等分点，依次连接.
启示：如何作圆内接正n边形？
找到正n边形的中心角，就找到了圆的等分点.顺次连接即可.
例2.（课本17页例12）如图，△ABC为圆内接正三角形，若圆的半径为r,求这个正三角形的边长和边心距.
分析：在图形中作出中心、半径、边心距.
半径：边心距：BD:∠BOD:∠OBD:
解：取中心O,连接OB,作OD⊥BC于D∵△ABC是等边三角形∴∠ABD=60°在Rt△OBD中
例2：（拓展）有一个亭子,它的地基是半径为4 m的正六边形,求地基的周长和面积 .
数学问题：已知正六边形ABCDEF的边长是4米，求它的周长和面积 .
分析：已知边长，周长易求；求面积时还需用到边心距，因此解决问题的关键是要求出边心距.
在Rt△OMB中,OB＝4,∠BOM=30°
解：连接OB,OC过点O作OM⊥BC于M.
利用勾股定理,可得边心距
2.作边心距，构造直角三角形.
1.连半径，得中心角；
正多边形中计算题的常用辅助线：
2. 要用圆形铁片截出边长为4cm的正方形铁片，则选用的圆形铁片的直径最小要____cm.
也就是要找这个正方形外接圆的直径，即正方形的对角线.
3.如图,M,N分别是⊙O内接正多边形AB,BC上的点,且BM=CN.(1)求图①中∠MON=________; 图②中∠MON= ; 图③中∠MON= ;
3.如图,M,N分别是⊙O内接正多边形AB,BC上的点,且BM=CN.(2)试探究∠MON的度数与正n边形的边数n的关系.
BM=CN,∠MBO=∠NCO,OB=OC
思考：四边形MONB的面积与正n边形的面积有什么关系？
正多边形的定义与对称性
正多边形的有关概念及性质
添加辅助线的方法：连半径，作边心距