初中数学人教版九年级下册27.2.1 相似三角形的判定授课课件ppt

这是一份初中数学人教版九年级下册27.2.1 相似三角形的判定授课课件ppt，共10页。PPT课件主要包含了等于k，∠B∠B，∠C∠C，∠A＝∠A，∴DEBC，解1∵，又∠A＝∠A，∠A∠A，∠ACB∠ECD，∴△ACB∽△ECD等内容，欢迎下载使用。
类似于判定三角形全等的SAS方法，我们能不能通过两边和夹角来判断两个三角形相似呢？
利用刻度尺和量角器画△ABC和△A'B'C'，使∠A＝∠A'， 和 都等于给定的值k，量出它们的第三组对应边BC和B'C'的长，它们的比等于k吗？另外两组对应角∠B与∠B'，∠C与∠C'是否相等？
改变∠A或K值的大小，再试一试，是否有同样的结论？
实际上，我们有利用两边和夹角判定两个三角形相似的方法：
改变k的值具有相同的结论
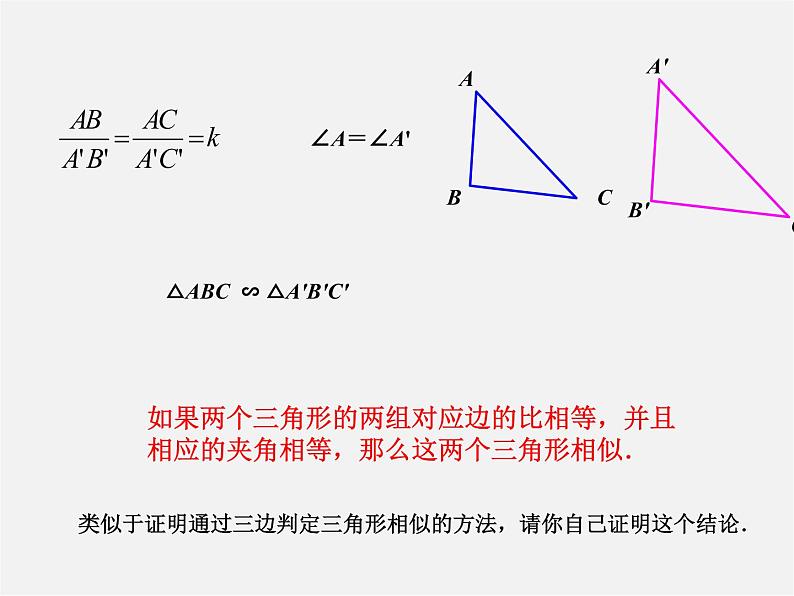
△ABC ∽ △A'B'C'
如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似．
类似于证明通过三边判定三角形相似的方法，请你自己证明这个结论．
已知：如图， △A'B'C'和 △ABC中，∠A ' =∠A，A'B'：AB＝A'C'：AC
求证：△A'B'C' ∽ △ABC
证明：在△ABC 的边AB、AC（或它们的延长线）上别截取AD＝A'B'，AE＝A'C'，连结DE，因∠A ' =∠A，这样△A'B'C' ≌ △ADE
∴ △ADE ∽ △ABC
∴ △A'B'C' ∽ △ABC
对于△ABC和△A'B'C'，如果 ∠B＝∠B'，这两个三角形一定相似吗？试着画画看．
不 一 定 相 似
根据下列条件，判断△ABC与△A'B'C'是否相似，并说明理由：（1）∠A＝120°，AB＝7cm，AC＝14cm， ∠A'＝120°，A'B'＝3cm，A'C'＝6cm；（2）AB＝4cm，BC＝6cm，AC＝8cm． 'B'＝12cm，B'C'＝18cm，A'C'＝21cm
∴ △ABC∽△A'B'C'
△ABC与△A'B'C'的三组对应边的比不等，它们不相似
两三角形的相似比是多少？
要使两三角形相似，不改变AC的长，A'C'的长应当改为多少？
1.根据下列条件，判断△ABC与△A'B'C'是否相似，并说明理由： （1）∠A=40°，AB=8，AC=15 ∠A' =40°，A'B' =16，A'C' =30 （2）AB=10cm，BC=8cm，AC=16cm A'B' =16cm，B'C' =12.8cm，A'C' =25.6cm
∴△ABC∽△A'B'C'
2. 图中的两个三角形是否相似？
∴图中两个三角形不相似．