初中数学人教版九年级下册27.2.1 相似三角形的判定备课课件ppt

这是一份初中数学人教版九年级下册27.2.1 相似三角形的判定备课课件ppt，共26页。PPT课件主要包含了复习提问，求证∠1∠2等内容，欢迎下载使用。

问题1：三角形全等的定义与判定方法？
三角形全等的定义：三组对应角相等，三组对应边相等。
问题2：我们如何判定两个三角形相似？
判定方法：SSS、SAS、ASA、AAS、 HL（适合于直角三角形）
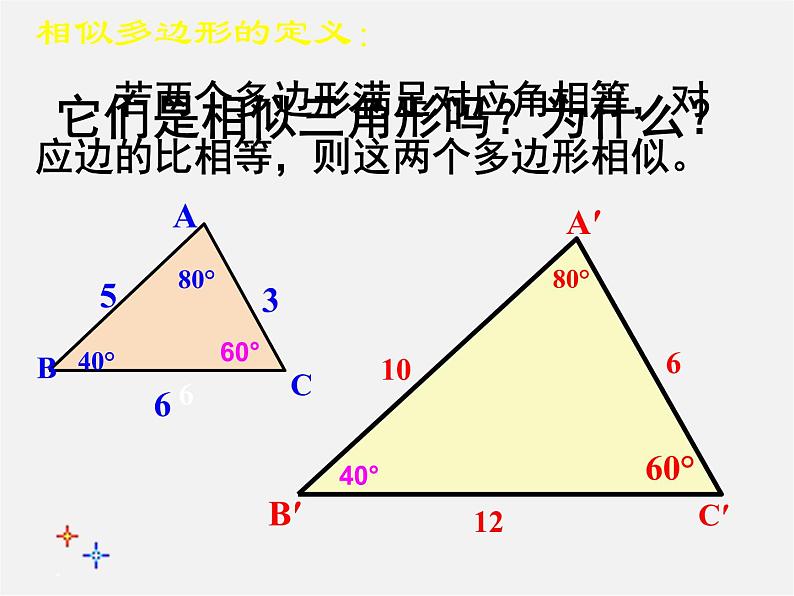
它们是相似三角形吗？为什么？
若两个多边形满足对应角相等，对应边的比相等，则这两个多边形相似。
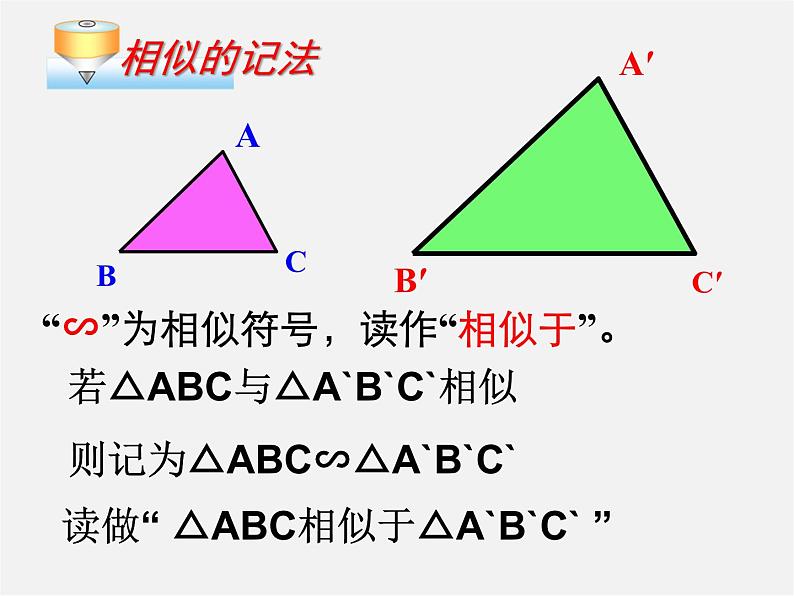
“∽”为相似符号，读作“相似于”。
若△ABC与△A`B`C`相似
则记为△ABC∽△A`B`C`
读做“ △ABC相似于△A`B`C` ”
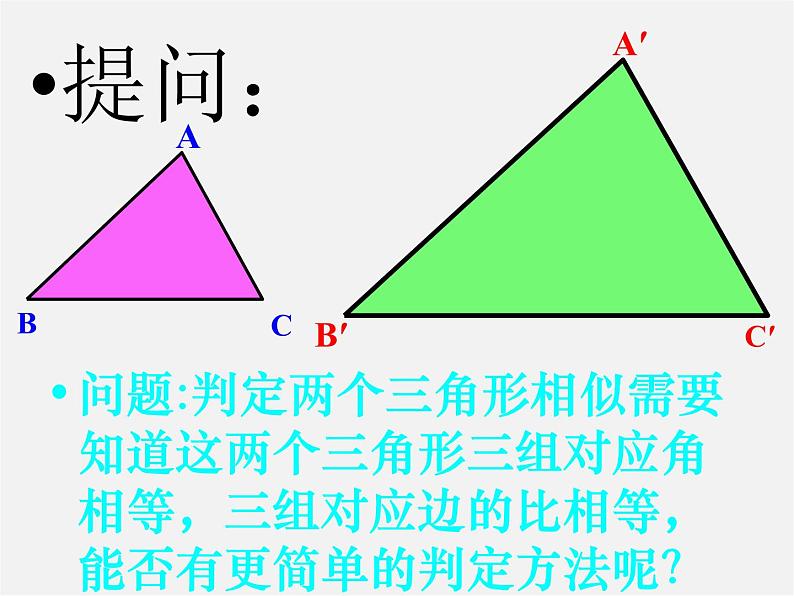
问题:判定两个三角形相似需要知道这两个三角形三组对应角相等，三组对应边的比相等，能否有更简单的判定方法呢？
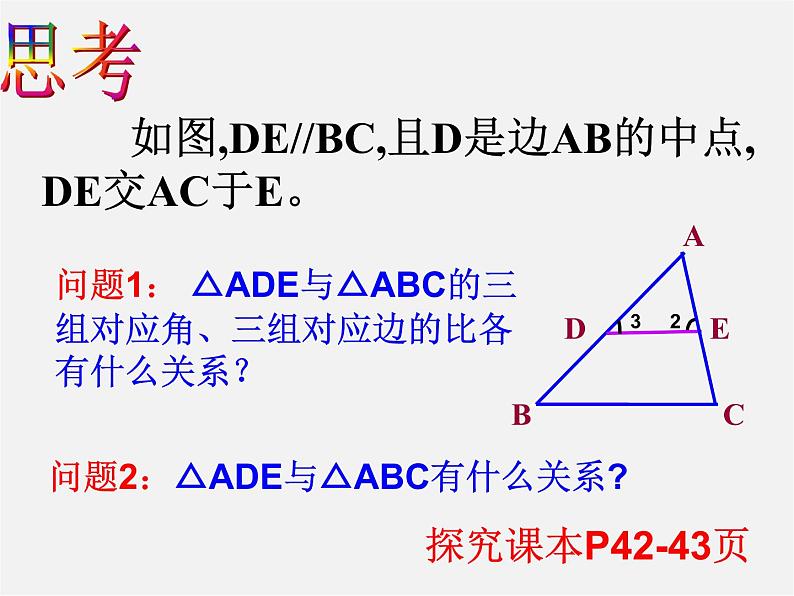
如图,DE//BC,且D是边AB的中点,DE交AC于E。
问题1： △ADE与△ABC的三组对应角、三组对应边的比各有什么关系？
问题2：△ADE与△ABC有什么关系?
探究课本P42-43页
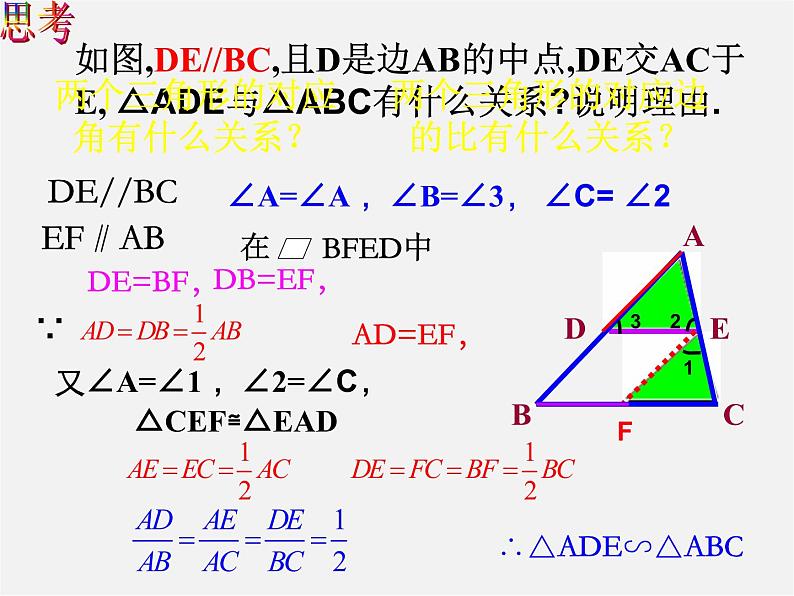
如图,DE//BC,且D是边AB的中点,DE交AC于E, △ADE与△ABC有什么关系?说明理由.
∠A=∠A ，∠B=∠3， ∠C= ∠2
又∠A=∠1 ，∠2=∠C，
两个三角形的对应边的比有什么关系？
两个三角形的对应角有什么关系？
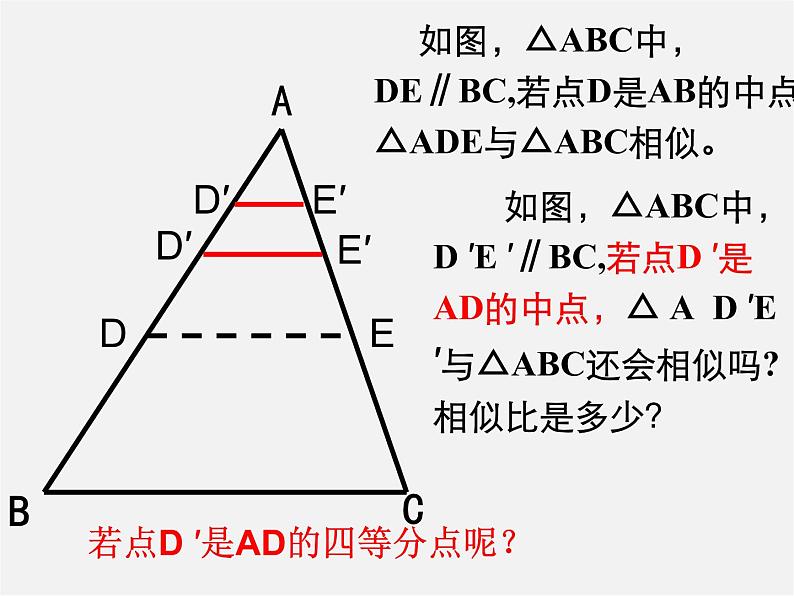
如图，△ABC中， DE∥BC,若点D是AB的中点，△ADE与△ABC相似。
如图，△ABC中， D ′E ′∥BC,若点D ′是AD的中点，△ A D ′E ′与△ABC还会相似吗?相似比是多少？
若点D ′是AD的四等分点呢？
如图，△ABC中， DE∥BC,若点D不是AB的中点，△ADE与△ABC还会相似吗?
△ADE与△ABC仍相似.
判定三角形相似定理： 平行于三角形一边的直线与其它两边(或两边延长线)相交,所得的三角形与原三角形相似。
1、下列各图都满足DE∥BC，是否都有△ADE∽△ABC？
2、 如图，在△ABC中，DG∥EH∥FI∥BC，如果AD=1，DB=3，那么DG：BC= _____ 。
3、如图,已知 DE∥BC,AE=40cm,EC=20cm, BC=48cm,∠A=450,∠C=400. (1)求∠ 1 和 ∠ 2 的大小; (2)求DE的长.
例如：画一个三角形使边长为：1cm、2cm、2.5cm ，再画一个三角形，使它的各边长都是这个三角形各边长的2或3倍。
请观察两个三角形的三组对应边有什么特点？
相似三角形判定定理： 如果两个三角形的三组对应边的比相等，那么这两个三角形相似。
任画一个三角形，再画一个三角形，使它的各边长都是原来三角形各边长的k倍(任确定一个倍数)，度量两个三角形的对应角，它们相等吗？这样的两个三角形相似吗？
在线段A`B`上截取A`D=AB过点D作DE∥ B`C` ，交A`C`于点E.
已知:如图△ABC和△A`B`C`中求证:△ABC∽△A`B`C`
△A`DE∽△A`B`C`
△ABC∽△A`B`C`
相似三角形判定定理：如果两个三角形的三组对应边的比相等，那么这两个三角形相似。
∴△ABC∽△A`B`C`
反馈练习1、试判定△ABC与A′B′C′是否相似，并说明理由．在△ABC和△A′B′C′中，已知：(1)AB＝6 cm， BC＝8 cm，AC＝10 cm，A′B′＝18 cm，B′C′＝24 cm，A′C′＝30 cm．
相似，因为对应边的比相等.
(2) AB=12cm， BC=15cm， AC＝24cm A′B′＝16cm，B′C′＝20cm，A′C′＝30cm
反馈练习试判定△ABC与A′B′C′是否相似，并说明理由．在△ABC和△A′B′C′中，已知：
不相似，因为对应边的比不相等.
∴ △ABC∽△ADE
∴ ∠BAC=∠DAE
∴ ∠BAC- ∠3 =∠DAE-∠3
课本：习题27.2 2（1）、3（1）、5选做题：练习册相应练习