人教版九年级下册27.1 图形的相似课文配套ppt课件

这是一份人教版九年级下册27.1 图形的相似课文配套ppt课件，共22页。PPT课件主要包含了“A”型，“X”型等内容，欢迎下载使用。
三条平行线截两条直线,所得的对应线段的比相等.
平行线分线段成比例定理：
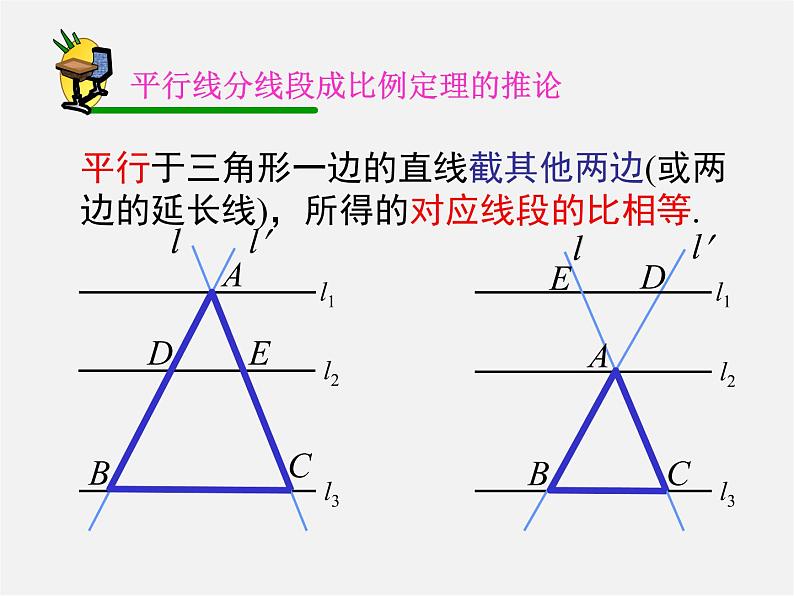
平行于三角形一边的直线截其他两边(或两边的延长线)，所得的对应线段的比相等.
平行线分线段成比例定理的推论
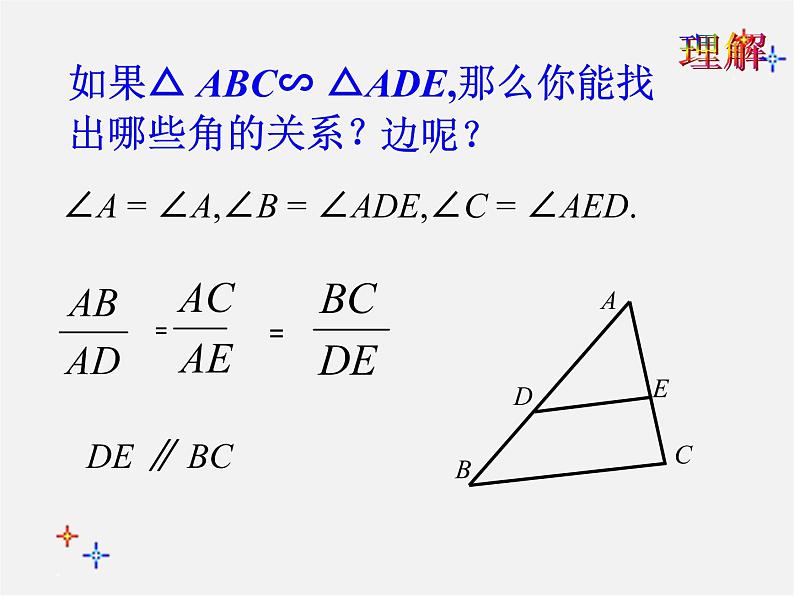
如果△ ABC∽ △ADE,那么你能找出哪些角的关系？
∠A = ∠A,∠B = ∠ADE,∠C = ∠AED.
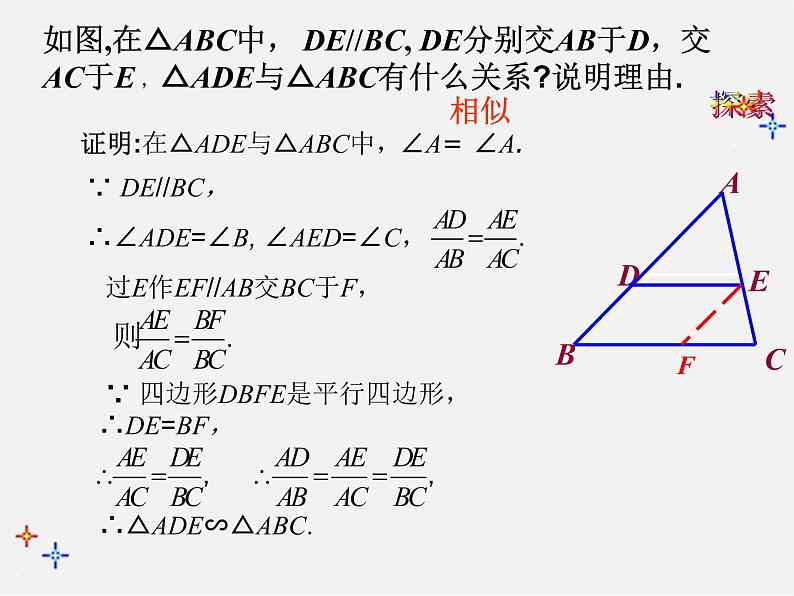
如图,在△ABC中， DE//BC, DE分别交AB于D，交AC于E ，△ADE与△ABC有什么关系?说明理由.
证明:在△ADE与△ABC中，
∴∠ADE=∠B, ∠AED=∠C，
过E作EF//AB交BC于F，
∵ 四边形DBFE是平行四边形，
∴△ADE∽△ABC.
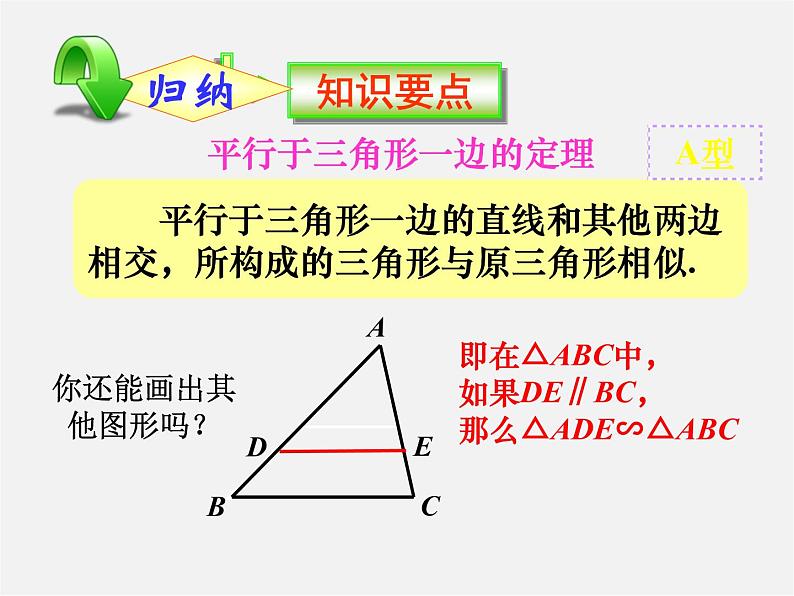
平行于三角形一边的定理
即在△ABC中，如果DE∥BC，那么△ADE∽△ABC
你还能画出其他图形吗？
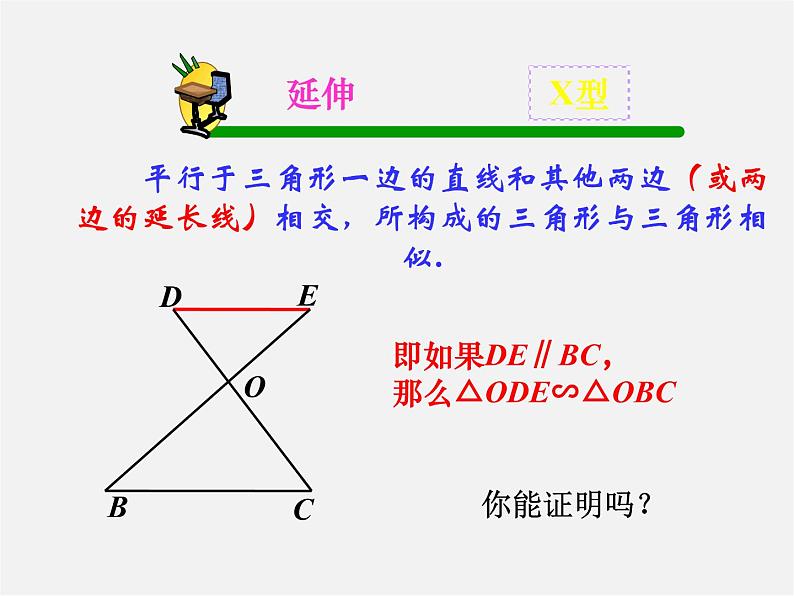
平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与三角形相似.
即如果DE∥BC，那么△ODE∽△OBC
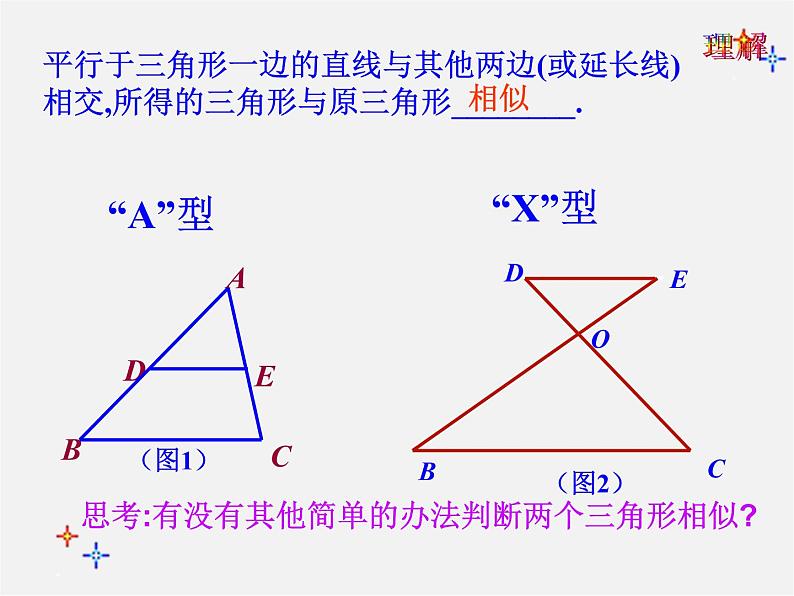
平行于三角形一边的直线与其他两边(或延长线)相交,所得的三角形与原三角形________.
思考:有没有其他简单的办法判断两个三角形相似?
任意画一个三角形，再画一个三角形，使它的各边长都是原来三角形各边长的k倍，度量这两个三角形的对应角，它们相等吗？这两个三角形相似吗？与同桌交流一下，看看是否有同样的结论.
是否有△ABC∽△A′B′C′？
求证: △ .
如果两个三角形的三组对应边的比相等，那么这两个三角形相似.
判定三角形相似的定理之一
△ABC∽△A′B′C′.
三边对应成比例，两三角形相似.
改变k和∠A的值的大小,是否有同样的结论？
△ABC∽△A′B′ C′.
如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似.
判定三角形相似的定理之二
两边对应成比例，且夹角相等，两三角形相似.
△ABC∽△A1B1C1.
不会，因为不能证明构造的三角形和原三角形全等.
A
B
C
这两个三角形一定会相似吗？
两个三角形的相似比是多少？
的三组对应边的比不等，它们不相似.
要使两个三角形相似，不改变AC的长，A′C′的长应改为多少？
例2 已知：如图，在四边形ABCD中，∠B=∠ACD，AB=6，BC=4，AC=5，CD= ，求AD的长.
解: AB=6，BC=4，AC=5，CD=
又∠B=∠ACD，
相似三角形的判定方法有几种？
3.边边边判定法（SSS）
4.边角边判定法（SAS）
只能在特定的图形里面使用