初中数学6 完全平方公式图片课件ppt

这是一份初中数学6 完全平方公式图片课件ppt，共21页。PPT课件主要包含了完全平方公式，教材分析，教材的地位和作用，教学重难点，学情教法，教学设计，附板书设计，教学反思等内容，欢迎下载使用。
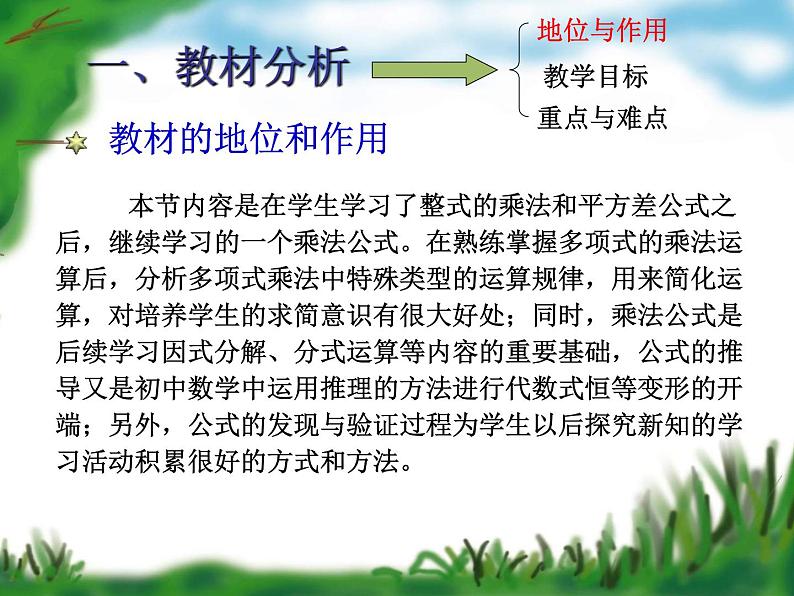
　　 本节内容是在学生学习了整式的乘法和平方差公式之后，继续学习的一个乘法公式。在熟练掌握多项式的乘法运算后，分析多项式乘法中特殊类型的运算规律，用来简化运算，对培养学生的求简意识有很大好处；同时，乘法公式是后续学习因式分解、分式运算等内容的重要基础，公式的推导又是初中数学中运用推理的方法进行代数式恒等变形的开端；另外，公式的发现与验证过程为学生以后探究新知的学习活动积累很好的方式和方法。
　　数学公式是数学中重要的基础知识，利用公式进行计算是重要的基本技能。怎样让学生经历公式发现和提炼的过程，感悟其作为公式的合理性，使学生进一步感受数形结合的魅力，从代数推理和几何背景等多角度探索公式，在深入理解的基础上灵活运用公式，是我这节课教学研究的重点。所以我确定以下教学目标：
1、知识与技能：会推导完全平方公式，并能运用公式进行简单的计算,进一步发展符号感和推理能力；了解完全平方公式的几何背景，感受数与形之间的联系，培养学生用图形解释数的能力及创造性思维和表达能力。
2、过程与方法：经历探索完全平方公式的全过程， 培养学生观察、发现、猜想、验证、推理等多种探 索知识的方法，从中渗透转化、化归、数形结合思想，培养学生求简意识，应用意识及辩证统一观念。
3、情感态度与价值观：通过反思问题情境的创设， 体验数学活动充满探索与发现，激发学生探索的热情，并鼓励学生探索算法的多样化，体会到解决问题策略的多样性，积累探索数学公式的学习经验，从中感受数学公式的简洁美，进一步提高学生的参与意识和合作精神。
　　 抽象的数学公式的教学，不仅要重视它的运用，更要关注它的实际背景与形成过程，才能有效地帮助学生克服机械地记忆、模仿和套用公式。只有让学生经历公式的发现和验证的过程，才能更好地理解、掌握和运用公式。
重点：经历完全平方公式的探索过程, 理解公式的 结构特点、语言描述和几何背景，并会运用 公式进行简单计算。
　　于是，我决定改变教学思路，从学生的错误猜想中切入，提出问题:(a+b)2=a2+b2 ?引导学生先自主探索 (a+b)2=a2+b2+2ab发现与验证的过程，再类比猜想、验证 (a－b)2=? 然后进行合作交流运用公式。在错误的反思中学习新知。
环节一：创设情景　引新设疑
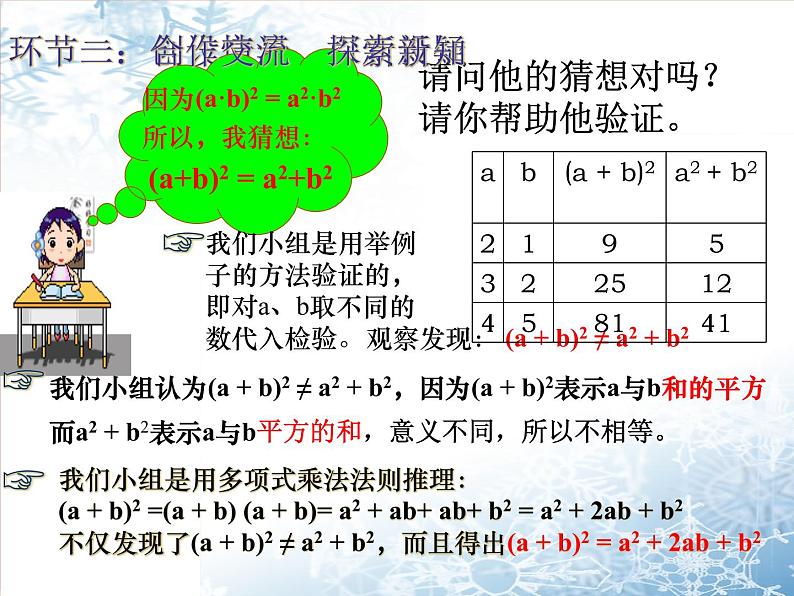
请问他的猜想对吗？请你帮助他验证。
我们小组认为(a + b)2 ≠ a2 + b2，因为(a + b)2表示a与b和的平方而a2 + b2表示a与b平方的和，意义不同，所以不相等。
环节二：合作交流　探索新知
这是我们学校门口那个边长为a米的正方形花坛，现要进行扩建，将它的边长增加b米，你有哪些方法求出扩建后的正方形花坛的面积？比一比看谁方法多？
如何用图形来验证公式:(a + b)2 = a2 + 2ab + b2 ?
S大=S小+2S梯 = a2+2× (a+a+b)b = a2+ 2ab+ b2
运用公式计算：① (x + 1)2 ② (2x +3)2　③ (mn + a)2 在小组内交流计算结果
你做对了吗?需要帮助吗?
环节三：参与其中 体验特征
两数和的完全平方公式：(a + b)2 = a2 + 2ab+b2
环节四：类比猜想　继续探索
请你猜猜(a －b)2 = ?能验证你的猜想吗？
你能运用公式(a +b)2 = a2 +2ab + b2计算(a －b)2=?
两数和(或差)的完全平方公式：(a +b)2 = a2 +2ab + b2(a－b)2 = a2－2ab + b2
编成口诀吧!顺口又好记!
和平方、差平方等于首平方、尾平方， 首尾乘积的2倍在中央。
(a－b)2=［a+（－b)］2 = a2 + 2a(-b)+(- b)2 = a2－2ab+ b2
都有a2 + b2，只是2ab符号不同，和(差)平方取正(负)； (a+b)2=(a－b)2 +4ab、 (a－b)2=(a＋b)2 －4ab ……
环节五：变式训练　感悟应用
例1：计算 ① (2x +3y)2　 ② ( 3x－2y)2 ③ (－2t+1)2　 ④ (－2t－1)2
( + )2=( )2+2× × +( )2 =4x2+12xy+9y2
学生做出了如下多种解法：( -2t－1)2=［( -2t)+(-1)］2 =( -2t)2+2×( -2t)×(-1)+(-1)2=4t2+4t+1( -2t－1)2=［( -2t)－(+1)］2=( -2t)2－2×( -2t)×1+12 =4t2+4t+1( -2t－1)2=［- (2t + 1)］2 = (2t+1)2 =(2t)2+2×2t×1+12=4t2+4t+1
(a+b)2 = a2 +2× a ×b +b2
环节五、变式训练 体验特征
例2、明辨是非，知错能改。①(a + 1)2 = a2 + 1 （ ） ②(a－1)2 = a2 － 1 （ ） ③(a + 2)2 = a2 + 2a +4 （ ） ④(2a－1)2 =2a2－2a + 1 （ ） ⑤(a－2)2 = a2－4a－ 4 （ ） ⑥(a－2b)2 = a2－2ab +2b2 （ ）
畅谈解题心得：要认准a、b； 注意乘积时添括号(2b)2； 小心别漏了2ab项；别忘了中间项乘2； 要先确定是和平方还是差平方；结果有三项，别犯(a+b)2＝a2 + b2 ，(a－b)2＝a2－b2错误……课堂练习: 计算:
环节六、学会评价　布置作业
畅谈本节课你学到哪些知识和方法？ 评价你自己的学习表现有哪些长处和不足？在小组活动中，你的同伴谁最优秀，他有 哪些优点值得你学习？并填写成长记录卡。
作业 A、必做作业：课本P43习题中“知识技能”1、2；B、选做作业：课本P43习题中“联系拓展”1、2；C、提高作业：思考(a+b)3=？(a+b)4 =？D、阅读作业：课本P41读一读“杨辉三角”。
让“不同的人在数学上得到不同的发展”.
符合评价方式采用定性和定量相结合的原则
猜想：(a + b)2 ≠ a2 + b2 ?猜想：(a －b)2 ≠ a2－b2 ?
(a + b)2 = a2 +2ab + b2(a－b)2 = a2－2ab + b2
两数和(或差)的完全平方公式
让反思贯穿于数学学习的始终，是本节课的特色。一开始通过学生对错误的类比猜想的式子进行反思、验证，明确了问题，激发了探究热情；在找到结论后，又通过对结论的反思，初步感受到将结论固化为公式的合理性；在运用公式解题时，又及时反思其特点和运用方法，概括为口诀；最后又让学生在找错误中反思其错误原因，畅谈解题心得。整个学习从反思中开始，在反思中结束。
　　通过本节课的教学实践，我再次体会到：教师是用教材教，而不是教教材，要注重挖掘教材中知识与能力的生长点和切入点。本节课教学中我没有将重点放在公式的大量练习上，而是更多地关注公式的发现和探索过程，让学生充分经历了知识形成过程，转变了学生的学习方式，培养了学生的学习能力，这正是新课程标准提倡的教学方法。　本节课以提高学生的学习能力和数学素养为指导思想，以学生积极参与数学活动为目标，以公式探索为载体，以猜想、验证与反思为主线，让学生在轻松愉悦的气氛中获取知识、掌握方法！整个教学既突出了学生的主体地位，又发挥了教师的指导作用。
两个班完成调查作业情况对比表
调 查 作 业 老师发现同学们在学完《整式乘法》这一章的各种公式后，在作业中总是出现各种各样的错误，不知是不是我们在公式教学中存在不足，还是同学们思维定势的影响，为了查清原因，改进方法，特向大家作一调查，请把你的真实情况反馈给我们，也许你“不小心”的错误对我们有很大的启发。 班级 姓名 座号_______
一、判别正误（对的打√，错的打×）1、(2 a)2 = 22·a2 = 4a2 ( ) 2、 ( ) 2 = = （ ）3、(m·n)2 = m2·n2 ( ) 4、(m÷n)2 = m2÷n2 ( )5、(m+n)2 = m2+n2 ( ) 6、(m－n)2 = m2－n2 （ ）
二、填空5、 (2+a)2 = 6、(a－2)2 = ———— 7 、(ab+1)2 = 8、(x+ )2 =　———— 三、计算9、 (2x－3y)2 10、(－a－b)2 11、(－a+b)2 四、判断正误（对的打√,错的打×，有错就改， 改在横线上）12、(a+2)2 = a2+2a+4 （ ）________13、(2a+1)2 = 4a2+1 ( ) _______14、(2a－1)2 = 2a2－2a+1 ( ) _______15、(a－3)2 = a2－9 ( ) ________16、(x－5)2 = x2－10x－25 ( ) _______五、你有哪些方法得出 (a+b)2 =？ (a－b)2 =？ （方法写在背面，看谁方法多）