人教A版 (2019)必修 第一册4.2 指数函数第1课时学案

这是一份人教A版 (2019)必修 第一册4.2 指数函数第1课时学案，共11页。学案主要包含了二象限，不可能出现在第三，指数函数的图象及应用等内容，欢迎下载使用。

4．2.2　指数函数的图象和性质
第1课时　指数函数的图象和性质(一)
学习目标　1.掌握指数函数的图象和性质.2.学会利用指数函数的图象和性质求函数的定义域、值域．

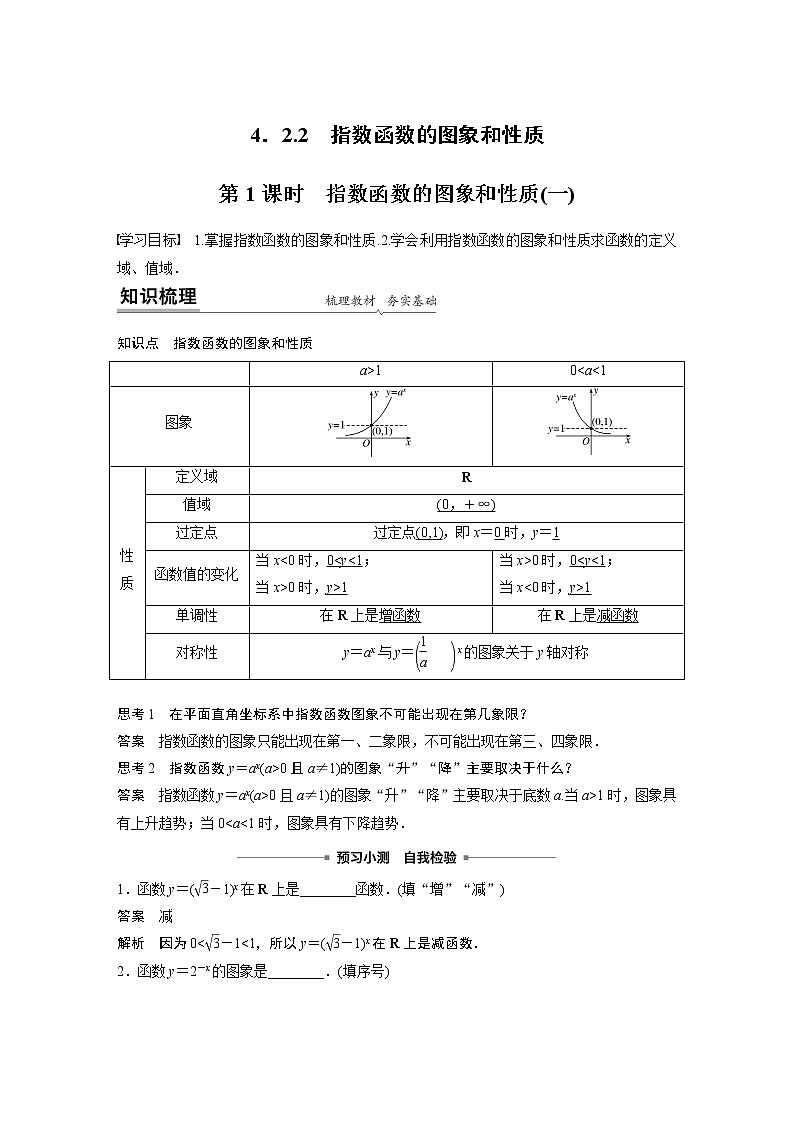
知识点　指数函数的图象和性质

a>1
0 图象


性质
定义域
R
值域
(0，＋∞)
过定点
过定点(0,1)，即x＝0时，y＝1
函数值的变化
当x<0时，0 当x>0时，y>1
当x>0时，0 当x<0时，y>1
单调性
在R上是增函数
在R上是减函数
对称性
y＝ax与y＝x的图象关于y轴对称

思考1　在平面直角坐标系中指数函数图象不可能出现在第几象限？
答案　指数函数的图象只能出现在第一、二象限，不可能出现在第三、四象限．
思考2　指数函数y＝ax(a>0且a≠1)的图象“升”“降”主要取决于什么？
答案　指数函数y＝ax(a>0且a≠1)的图象“升”“降”主要取决于底数a.当a>1时，图象具有上升趋势；当0
1．函数y＝(－1)x在R上是________函数．(填“增”“减”)
答案　减
解析　因为0<－1<1，所以y＝(－1)x在R上是减函数．
2．函数y＝2－x的图象是________．(填序号)

答案　②
解析　y＝2－x＝x是减函数，排除①③，
又过点(0,1)，排除④.
3．函数y＝ax(a>0且a≠1)在R上是增函数，则a的取值范围是________．
答案　(1，＋∞)
解析　结合指数函数的性质可知，若y＝ax(a>0且a≠1)在R上是增函数，则a>1.
4．函数f(x)＝2x＋3的值域为________．
答案　(3，＋∞)
解析　因为2x>0，所以2x＋3>3，
即函数f(x)＝2x＋3的值域为(3，＋∞)．

一、指数函数的定义域和值域
例1　求下列函数的定义域和值域：
(1)y＝－|x|；
(2)y＝；
(3) y＝4x－2x＋1.
解　(1)定义域为R.
∵|x|≥0，∴y＝－|x|＝|x|≥0＝1，∴此函数的值域为[1，＋∞)．
(2)由题意知1－x≥0，∴x≤1＝0，
∴x≥0，∴定义域为[0，＋∞)．
∵x≥0，∴x≤1.
又∵x>0，∴0 ∴0≤y<1，∴此函数的值域为[0,1)．
(3)函数的定义域为R.
y＝(2x)2－2x＋1＝2＋，
∵2x>0，∴当2x＝，即x＝－1时，y取最小值，
∴函数的值域为.
(教师)
延伸探究
本例(3)的函数变为“y＝4x－2x＋1，x∈[0,2]”，求其值域．
解　y＝(2x)2－2x＋1＝2＋，
∵x∈[0,2]，∴2x∈[1,4]，
∴当2x＝1，即x＝0时，y取最小值1；
∴当2x＝4，即x＝2时，y取最大值13，
∴函数的值域为[1,13]．
反思感悟　函数y＝af(x)定义域、值域的求法
(1)定义域：形如y＝af(x)形式的函数的定义域是使得f(x)有意义的x的取值集合．
(2)值域：①换元，令t＝f(x)；
②求t＝f(x)的定义域x∈D；
③求t＝f(x)的值域t∈M；
④利用y＝at的单调性求y＝at，t∈M的值域．
注意：(1)通过建立不等关系求定义域时，要注意解集为各不等关系解集的交集．
(2)当指数型函数的底数含字母时，在求定义域、值域时要注意分类讨论．
跟踪训练1　求下列函数的定义域、值域：
(1)y＝；
(2) y＝.
解　(1)函数的定义域为R.
∵y＝＝＝1－，
又∵3x>0，∴1＋3x>1，∴0<<1，
∴－1<－<0，
∴0<1－<1，∴函数的值域为(0,1)．
(2) x应满足x－4≠0，∴x≠4，
∴定义域为{x|x≠4，x∈R}．
∵≠0，∴≠1，
∴y＝的值域为{y|y>0，且y≠1}．
二、指数函数的图象及应用
例2　(1)已知0
答案　C
解析　由于0 (2)函数f(x)＝ax－b的图象如图所示，其中a，b为常数，则下列结论正确的是(　　)

A．a>1，b<0
B．a>1，b>0
C．00
D．0 答案　D
解析　从曲线的变化趋势，可以得到函数f(x)为减函数，从而有00，即b<0.
(3)已知函数y＝3x的图象，怎样变换得到y＝x＋1＋2的图象？并画出相应图象．
解　y＝x＋1＋2＝3－(x＋1)＋2.作函数y＝3x关于y轴的对称图象得函数y＝3－x的图象，再向左平移1个单位长度就得到函数y＝3－(x＋1)的图象，最后再向上平移2个单位长度就得到函数y＝3－(x＋1)＋2＝x＋1＋2的图象，如图所示．

反思感悟　处理函数图象问题的策略
(1)抓住特殊点：指数函数的图象过定点(0,1)，求指数型函数图象所过的定点时，只要令指数为0，求出对应的x，y的值，即可得函数图象所过的定点．
(2)巧用图象变换：函数图象的平移变换(左右平移、上下平移)．
(3)利用函数的性质：奇偶性与单调性．
跟踪训练2　(1)函数f(x)＝2ax＋1－3(a>0，且a≠1)的图象恒过的定点是________．
答案　(－1，－1)
解析　因为y＝ax的图象过定点(0,1)，
所以令x＋1＝0，即x＝－1，
则f(－1)＝－1，
故f(x)＝2ax＋1－3的图象过定点(－1，－1)．
(2)已知直线y＝2a与函数y＝|2x－2|的图象有两个公共点，求实数a的取值范围．
解　函数y＝|2x－2|的图象如图所示．要使直线y＝2a与该图象有两个公共点，则有0<2a<2，即0

1．函数f(x)＝πx与g(x)＝x的图象关于(　　)
A．原点对称 B．x轴对称
C．y轴对称 D．直线y＝－x对称
答案　C
解析　设点(x，y)为函数f(x)＝πx的图象上任意一点，则点(－x，y)为g(x)＝π－x＝x的图象上的点．因为点(x，y)与点(－x，y)关于y轴对称，所以函数f(x)＝πx与g(x)＝x的图象关于y轴对称．
2.指数函数y＝ax与y＝bx的图象如图所示，则(　　)

A．a<0，b<0
B．a<0，b>0
C．01
D．0 答案　C
解析　结合指数函数图象的特点可知01.
3．函数f(x)＝2·ax－1＋1的图象恒过定点________．
答案　(1,3)
解析　令x－1＝0，得x＝1，f(1)＝2×1＋1＝3，
所以f(x)的图象恒过定点(1,3)．
4．函数y＝的定义域是________．
答案　[0，＋∞)
解析　由2x－1≥0解得x≥0，
所以函数y＝的定义域是[0，＋∞)．
5．函数f(x)＝x－1，x∈[－1,2]的值域为________．
答案　
解析　∵－1≤x≤2，∴≤x≤3.
∴－≤x－1≤2.
∴函数f(x)的值域为.

1．知识清单：
(1)指数函数的图象．
(2)指数函数的性质：定义域、值域、单调性及过定点．
2．方法归纳：数形结合法、换元法．
3．常见误区：在求值域时易忽视指数函数隐含的条件ax>0.


1．全集U＝R，集合A＝{x|y＝}，则∁UA等于(　　)
A．[0，＋∞) B．(－∞，0)
C．(0，＋∞) D．(－∞，0]
答案　C
解析　∵x－1≥0，∴x≥1＝0，
∴x≤0，A＝{x|x≤0}，∴∁UA＝{x|x>0}．
2．函数y＝的值域是(　　)
A．[0，＋∞) B．[0,4]
C．[0,4) D．(0,4)
答案　C
解析　要使函数有意义，须满足16－4x≥0.
又因为4x>0，所以0≤16－4x<16，
即函数y＝的值域为[0,4)．
3．函数y＝2x＋1的图象是(　　)

答案　A
解析　当x＝0时，y＝2，且函数单调递增．
4．(多选)若a>1，－1 A．第一象限 B．第二象限
C．第三象限 D．第四象限
答案　ABC
解析　∵a>1，且－1
5．函数f(x)＝ax与g(x)＝－x＋a的图象大致是(　　)

答案　A
解析　当a>1时，函数f(x)＝ax单调递增，当x＝0时，g(0)＝a>1，此时两函数的图象大致为选项A.
6．若0 答案　一
解析　函数y＝ax的图象过点(0,1)，向下平移|b|个单位长度，超过一个单位长度，所以函数f(x)＝ax＋b的图象不过第一象限．
7．若函数y＝x在[－2，－1]上的最大值为m，最小值为n，则m＋n＝________.
答案　6
解析　由指数函数y＝x的图象可知在x＝－1处取最小值为2，在x＝－2处取最大值为4.∴m＋n＝6.
8．若函数f(x)＝则函数f(x)的值域是________．
答案　(－1,0)∪(0,1)
解析　由x<0，得0<2x<1；
由x>0，∴－x<0,0<2－x<1，
∴－1<－2－x<0，
∴函数f(x)的值域为(－1,0)∪(0,1)．
9．已知函数f(x)＝ax(x≥0)的图象经过点，其中a>0且a≠1.
(1)求a的值；
(2)求函数y＝f(x)＋1(x≥0)的值域．
解　(1)因为函数f(x)＝ax(x≥0)的图象经过点，所以a2＝，a＝.
(2)由(1)得f(x)＝x(x≥0)，函数为减函数，
当x＝0时，函数取最大值1，故f(x)∈(0,1]，
所以函数y＝f(x)＋1＝x＋1(x≥0)∈(1,2]，
故函数y＝f(x)＋1(x≥0)的值域为(1,2]．
10．设f(x)＝3x，g(x)＝x.
(1)在同一坐标系中作出f(x)，g(x)的图象；
(2)计算f(1)与g(－1)，f(π)与g(－π)，f(m)与g(－m)的值，从中你能得到什么结论？
解　(1)函数f(x)，g(x)的图象如图所示，

(2)f(1)＝31＝3，g(－1)＝－1＝3，f(π)＝3π，
g(－π)＝－π＝3π，
f(m)＝3m，g(－m)＝－m＝3m.
从以上计算的结果看，两个函数当自变量取值互为相反数时，其函数值相等，即当指数函数的底数互为倒数时，它们的图象关于y轴对称．

11．函数y＝2－1的定义域、值域分别是(　　)
A．R，(0，＋∞)
B．{x|x≠0}，{y|y>－1}
C．{x|x≠0}，{y|y>－1，且y≠1}
D．{x|x≠0}，{y|y>－1，且y≠0}
答案　C
解析　要使y＝－1有意义，
只需有意义，即x≠0.
若令u＝＝1－，
则可知u≠1，∴y≠21－1＝1.
又∵y＝－1>0－1＝－1，
∴函数y＝－1的定义域为{x|x≠0}，值域为{y|y>－1，且y≠1}．
12．若函数y＝ax＋b－1(a>0，且a≠1)的图象经过第二、三、四象限，则一定有(　　)
A．00 B．a>1，且b>0
C．01，且b<0
答案　C
解析　函数y＝ax＋b－1(a>0，且a≠1)的图象是由函数y＝ax的图象经过向上或向下平移而得到的，因其图象不经过第一象限，所以a∈(0,1)．若经过第二、三、四象限，则需将函数y＝ax(0 13．函数f(x)＝的图象大致为(　　)

答案　B
解析　f(x)＝＝
由指数函数的图象知B正确．
14．已知实数a，b满足等式a＝b，给出下列五个关系式：①0 答案　2
解析　作y＝x与y＝x的图象(图略)．
当a＝b＝0时，a＝b＝1；
当a 当a>b>0时，也可以使a＝b.
故①②⑤都可能成立，不可能成立的关系式是③④.

15．已知函数f(x)＝(x－a)(x－b)(其中a>b)的图象如图所示，则函数g(x)＝ax＋b的图象是(　　)


答案　A
解析　由函数f(x)＝(x－a)(x－b)(其中a>b)的图象可知0 16．已知函数f(x)＝ax＋b(a>0，且a≠1)．
(1)若f(x)的图象如图①所示，求a，b的值；
(2)若f(x)的图象如图②所示，求a，b的取值范围；
(3)在(1)中，若|f(x)|＝m有且仅有一个实数根，求m的取值范围．

解　(1)f(x)的图象过点(2,0)，(0，－2)，
所以
又因为a>0，且a≠1，所以a＝，b＝－3.
(2)f(x)单调递减，所以0 又f(0)<0.即a0＋b<0，所以b<－1.
故a的取值范围为(0,1)，b的取值范围为(－∞，－1)．
(3)画出|f(x)|＝|()x－3|的图象如图所示，要使|f(x)|＝m有且仅有一个实数根，则m＝0或m≥3.
故m的取值范围为[3，＋∞)∪{0}．