人教A版 (2019)必修 第一册第四章 指数函数与对数函数本章综合与测试学案

这是一份人教A版 (2019)必修 第一册第四章 指数函数与对数函数本章综合与测试学案，共7页。

1．函数f(x)＝ax－1(a>0，a≠1)的图象恒过点A，下列函数中图象不经过点A的是( )
A．y＝eq \r(1－x) B．y＝|x－2|
C．y＝2x－1 D．y＝x2
答案 A
解析 函数f(x)过定点为(1,1)，代入选项验证可知A选项不过A点．
2．已知a＝0.70.5，b＝0.70.8，c＝(eq \r(2))0.8，则a，b，c的大小关系为( )
A．aC．c答案 D
解析 ∵函数y＝0.7x为R上的减函数，0.5<0.8，
∴1＝0.70>a＝0.70.5>b＝0.70.8，而1＝(eq \r(2))03．函数y＝e2－e|x|(e为无理数，且e≈2.718 28…)的图象可能是( )
答案 B
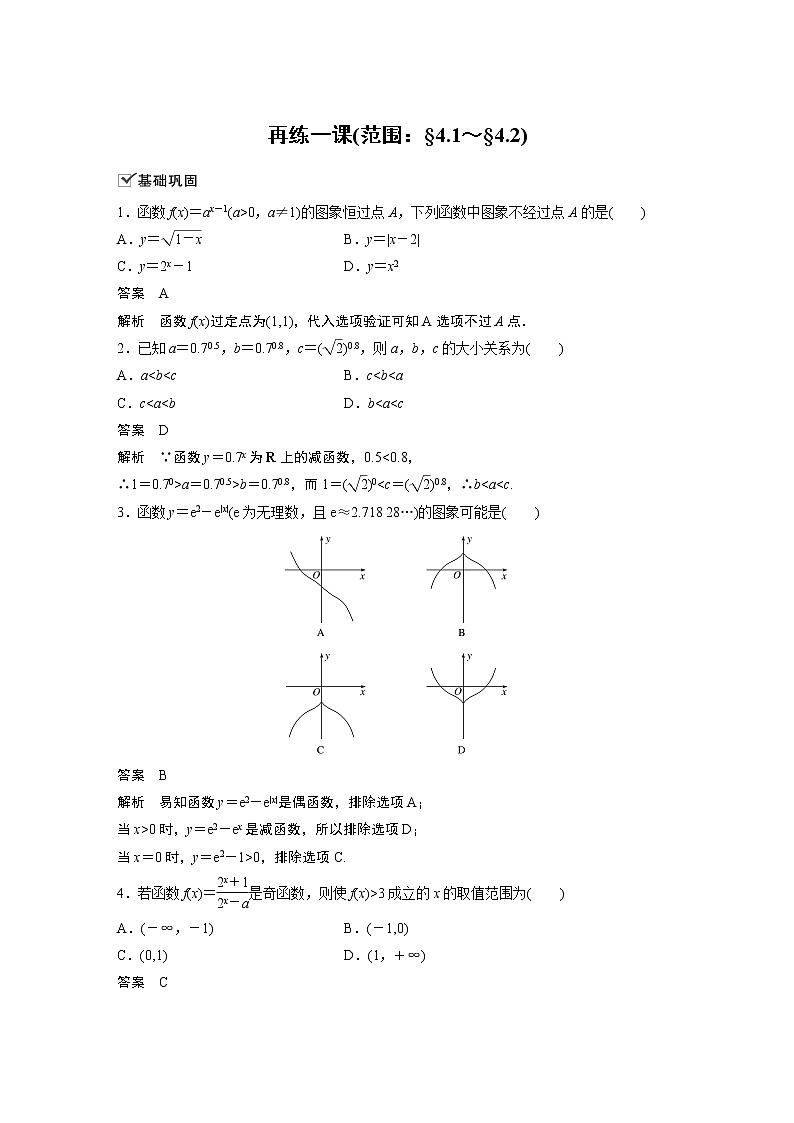
解析 易知函数y＝e2－e|x|是偶函数，排除选项A；
当x>0时，y＝e2－ex是减函数，所以排除选项D；
当x＝0时，y＝e2－1>0，排除选项C.
4．若函数f(x)＝eq \f(2x＋1,2x－a)是奇函数，则使f(x)>3成立的x的取值范围为( )
A．(－∞，－1) B．(－1,0)
C．(0,1) D．(1，＋∞)
答案 C
解析 ∵f(x)为奇函数，∴f(－x)＝－f(x)，即eq \f(2－x＋1,2－x－a)＝－eq \f(2x＋1,2x－a)，∴eq \f(2x＋1,1－a·2x)＝eq \f(2x＋1,a－2x)，∴a＝1，故f(x)＝eq \f(2x＋1,2x－1)(x≠0)，根据题意，令t＝2x，由f(x)>3可得eq \f(t＋1,t－1)>3⇔eq \f(t＋1,t－1)－3>0⇔eq \f(t－2,t－1)<0⇔15．(多选)已知函数f(x)＝eq \f(πx－π－x,2)，g(x)＝eq \f(πx＋π－x,2)，则f(x)，g(x)满足( )
A．f(－x)＋g(－x)＝g(x)－f(x)
B．f(－2)C．f(x)－g(x)＝π－x
D．f(2x)＝2f(x)g(x)
答案 ABD
解析 A正确，f(－x)＝eq \f(π－x－πx,2)＝－f(x)，
g(－x)＝eq \f(π－x＋πx,2)＝g(x)，
所以f(－x)＋g(－x)＝g(x)－f(x)；
B正确，因为函数f(x)为增函数，所以f(－2)C不正确，f(x)－g(x)＝eq \f(πx－π－x,2)－eq \f(πx＋π－x,2)＝eq \f(－2π－x,2)＝－π－x；
D正确，f(2x)＝eq \f(π2x－π－2x,2)＝2·eq \f(πx－π－x,2)·eq \f(πx＋π－x,2)＝2f(x)g(x)．
6．函数y＝3·ax－2＋1(a>0且a≠1)的图象必经过点________．
答案 (2,4)
解析 对于函数y＝3·ax－2＋1(a>0且a≠1)，
令x－2＝0，求得x＝2，y＝4，
可得它的图象经过定点(2,4)．
7．函数y＝的值域是________，单调递增区间是________．
答案 eq \b\lc\[\rc\](\a\vs4\al\c1(\f(1,2)，2))
解析 令t＝eq \r(－x2＋x＋2)＝eq \r(－x－2x＋1)
＝eq \r(－\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(1,2)))2＋\f(9,4))，
则0≤t≤eq \f(3,2)，∴y＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))t∈，
即函数y＝的值域是；
函数y＝的定义域为[－1,2]．
当0≤t≤eq \f(3,2)时，y＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))t单调递减，
当eq \f(1,2)≤x≤2时，函数t单调递减，
∴函数y的增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(1,2)，2)).
8．函数f(x)＝－9－x＋eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)))x－1＋eq \f(3,4)，x∈[－1，＋∞)的值域为________．
答案 eq \b\lc\[\rc\](\a\vs4\al\c1(\f(3,4)，3))
解析 f(x)＝－9－x＋eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)))x－1＋eq \f(3,4)
＝－eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)))2x＋3×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)))x＋eq \f(3,4)，
令t＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)))x，
因为x∈[－1，＋∞)，所以t∈(0,3]，
原函数的值域等价于函数g(t)＝－t2＋3t＋eq \f(3,4)＝－eq \b\lc\(\rc\)(\a\vs4\al\c1(t－\f(3,2)))2＋3(0所以g(t)在eq \b\lc\(\rc\](\a\vs4\al\c1(0，\f(3,2)))上单调递增，eq \b\lc\(\rc\](\a\vs4\al\c1(\f(3,2)，3))上单调递减，
geq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)))＝3，g(3)＝eq \f(3,4)，
所以f(x)∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(3,4)，3)).
9．若f(x)＝eq \f(2x＋a,2x－1)是奇函数．
(1)求a的值；
(2)若对任意x∈(0，＋∞)都有f(x)≥2m2－m，求实数m的取值范围．
解 (1)由题意得，f(x)的定义域为{x|x≠0}．
f(1)＝2＋a，f(－1)＝－1－2a，
因为f(x)＝eq \f(2x＋a,2x－1)是奇函数．
所以f(1)＝－f(－1)，得a＝1；经检验a＝1满足题意．
(2)根据(1)可知f(x)＝eq \f(2x＋1,2x－1)，
化简可得f(x)＝1＋eq \f(2,2x－1)，
当x∈(0，＋∞)时，f(x)>1，
对任意x∈(0，＋∞)都有f(x)≥2m2－m，
所以1≥2m2－m，即－eq \f(1,2)≤m≤1.
故m的取值范围为eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(1,2)，1)).
10．已知g(x)＝x2－2ax＋1在区间[1,3] 上的值域为[0,4]．
(1)求实数a的值；
(2)若不等式g(2x)－k·4x≥0在当x∈[1，＋∞)上恒成立，求实数k的取值范围．
解 (1)g(x)＝(x－a)2＋1－a2，
当a<1时，g(x)在[1,3]上单调递增，
∴g(x)min＝g(1)＝2－2a＝0，即a＝1，与a<1矛盾．故舍去．
当1≤a≤3时，g(x)min＝g(a)＝1－a2＝0，即a＝±1，故a＝1，
此时g(x)＝(x－1)2，满足x∈[1,3]时其函数值域为[0,4]．
当a>3时，g(x)在[1,3]上单调递减，
g(x)min＝g(3)＝10－6a＝0，即a＝eq \f(5,3)，舍去．
综上所述a＝1.
(2)由已知得(2x)2－2×2x＋1－k·4x≥0在x∈[1，＋∞)上恒成立，即 k≤eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2x)))2－2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2x)))＋1在x∈[1，＋∞)上恒成立，
令t＝eq \f(1,2x)，且t∈eq \b\lc\(\rc\](\a\vs4\al\c1(0，\f(1,2)))，则上式可化为k≤t2－2t＋1，t∈eq \b\lc\(\rc\](\a\vs4\al\c1(0，\f(1,2)))恒成立．记h(t)＝t2－2t＋1，
∵t∈eq \b\lc\(\rc\](\a\vs4\al\c1(0，\f(1,2)))时，h(t)单调递减，
∴h(t)min＝heq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))＝eq \f(1,4)，故k≤eq \f(1,4)，
∴k的取值范围为eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，\f(1,4))).
11．已知f(x)是定义在R上的偶函数，且在区间(－∞，0)上单调递增．若实数a满足f(2|a－1|)>
f(－eq \r(2))，则a的取值范围是( )
A.eq \b\lc\(\rc\)(\a\vs4\al\c1(－∞，\f(1,2)))
B.eq \b\lc\(\rc\)(\a\vs4\al\c1(－∞，\f(1,2)))∪eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)，＋∞))
C.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，\f(3,2)))
D.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)，＋∞))
答案 C
解析 由f(x)是定义在R上的偶函数且在区间(－∞，0)上单调递增，可知f(x)在区间(0，＋∞)上单调递减，∴由f(2|a－1|)>f(－eq \r(2))，f(－eq \r(2))＝f(eq \r(2))，可得2|a－1|12．已知实数a>0且a≠1，若函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(6－x，x≤2，,ax，x>2))的值域为[4，＋∞)，则a的取值范围是( )
A．(1,2) B．(2，＋∞)
C．(0,1)∪(1,2] D．[2，＋∞)
答案 D
解析 实数a>0且a≠1，若函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(6－x，x≤2，,ax，x>2))的值域为[4，＋∞)，
当02时，f(x)的取值范围为(0，a2)，与值域为[4，＋∞)矛盾，所以0当a>1时，对于函数f(x)＝6－x，x≤2，函数的值域为[4，＋∞)．所以只需当x>2时f(x)的取值范围为[4，＋∞)的子集即可．即a2≥4，解得a≥2(舍去a≤－2)，
综上可知a的取值范围为[2，＋∞)．
13．关于x的不等式a·9x＋2·3x－1<0对任意x>0恒成立，则实数a的取值范围是( )
A．a<－2 B．a≤－1
C．a≤－2 D．a<－1
答案 B
解析 ∵a·9x＋2·3x－1<0对任意x>0恒成立，
∴a∴a·9x＋2·3x－1<0对任意x>0恒成立等价于a∵t2－2t＝(t－1)2－1>－1，∴a≤－1.
14．已知函数f(x)＝2 019x－2 019－x＋1，则不等式f(2x－1)＋f(2x)>2的解集为________．
答案 eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,4)，＋∞))
解析 设g(x)＝f(x)－1＝2 019x－2 019－x，则g(－x)＝2 019－x－2 019x＝－g(x)，∴g(x)是奇函数，易知g(x)＝2 019x－2 019－x是R上的增函数．
由f(2x－1)＋f(2x)>2得f(2x－1)－1＋f(2x)－1>0，即g(2x－1)＋g(2x)>0，
∴g(2x－1)>g(－2x)，即2x－1>－2x，解得x>eq \f(1,4).
15．已知f(x)是定义在[－2,2]上的奇函数，当x∈(0,2]时，f(x)＝2x－1，函数g(x)＝x2－2x＋m，如果对于任意x1∈[－2,2]，存在x2∈[－2,2]，使得g(x2)＝f(x1)，则实数m的取值范围是( )
A．(－∞，－2) B．(－5，－2)
C．[－5，－2] D．(－∞，－2]
答案 C
解析 ∵f(x)是定义在[－2,2]上的奇函数，
∴f(0)＝0，
当x∈(0,2]时，f(x)＝2x－1∈(0,3]，
则当x∈[－2,2]时，f(x)∈[－3,3]，
若对于∀x1∈[－2,2]，∃x2∈[－2,2]，
使得g(x2)＝f(x1)，
则等价为g(x)max≥3且g(x)min≤－3，
∵g(x)＝x2－2x＋m＝(x－1)2＋m－1，x∈[－2,2]，
∴g(x)max＝g(－2)＝8＋m，g(x)min＝g(1)＝m－1，
则满足8＋m≥3且m－1≤－3，
解得m≥－5且m≤－2，故－5≤m≤－2.
16．已知函数f(x)＝.
(1)若a＝1，求f(x)的单调区间；
(2)若f(x)的最大值为3，求实数a的值；
(3)若f(x)的值域是(0，＋∞)，求实数a的值．
解 (1)当a＝1时，f(x)＝，
令g(x)＝x2－4x＋3，由于g(x)在(－∞，2)上单调递减，在(2，＋∞)上单调递增，
而y＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)))t在R上为减函数，
所以f(x)在(－∞，2)上单调递增，在(2，＋∞)上单调递减，
即函数f(x)的单调递减区间是(2，＋∞)，单调递增区间是(－∞，2)．
(2)令h(x)＝ax2－4x＋3，则f(x)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)))h(x)，
因为f(x)的最大值为3，所以h(x)的最小值为－1，
当a＝0时，f(x)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)))－4x＋3，无最大值；
当a≠0时，有eq \b\lc\{\rc\ (\a\vs4\al\c1(a>0，,\f(3a－4,a)＝－1，))解得a＝1，
所以当f(x)的最大值为3时，实数a的值为1.
(3)由指数函数的性质知，要使f(x)＝的值域为(0，＋∞)，
应使h(x)＝ax2－4x＋3的值域为R.
当a＝0时，h(x)＝－4x＋3，值域为R，符合题意；
当a≠0时，h(x)为二次函数，其值域不为R，不符合题意．
故当f(x)的值域是(0，＋∞)时，实数a的值为0.