北师大版七年级下册6 完全平方公式备课ppt课件

这是一份北师大版七年级下册6 完全平方公式备课ppt课件，共15页。PPT课件主要包含了a2−b2，平方差公式，a−b2，a+−b2，的证明，练一练，课堂小结，本节课你学到了什么等内容，欢迎下载使用。

对于一般两个二项式的积, 看准有无相等的“项”和符号相反的“项”;
仅当把两个二项式的积变成公式标准形式后，才能使用平方差公式。
(a+b)(a−b)=
即两数和与这两数差的积.
完 全 平 方 公 式
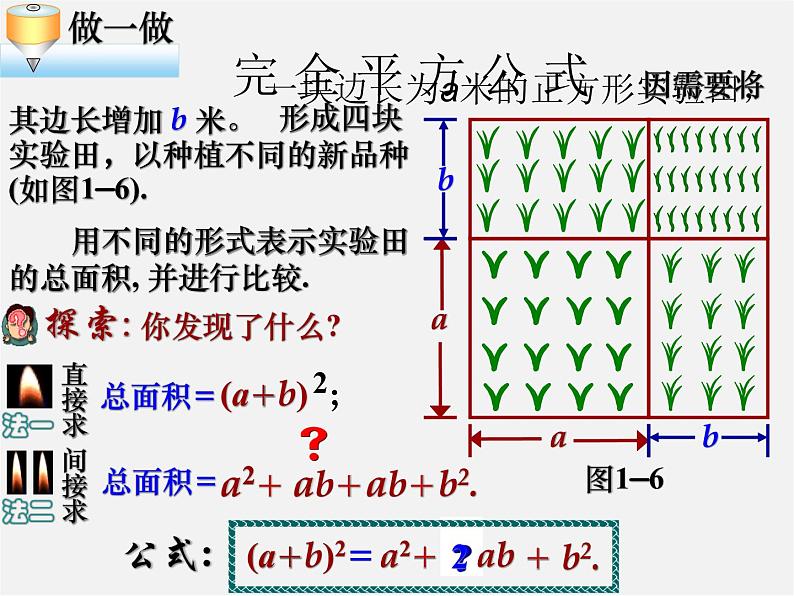
一块边长为a米的正方形实验田，
因需要将其边长增加 b 米。
形成四块实验田，以种植不同的新品种(如图1—6).
用不同的形式表示实验田的总面积, 并进行比较.
完全平方公式
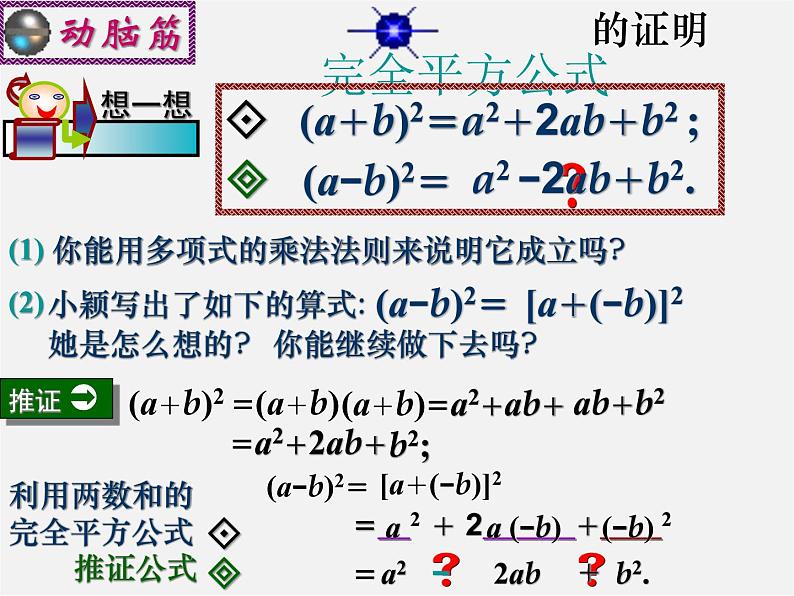
(1) 你能用多项式的乘法法则来说明它成立吗?
(a+b)2=a2+2ab+b2 ;
a2 −2ab+b2.
小颖写出了如下的算式:
利用两数和的完全平方公式
= 2 + 2 + 2
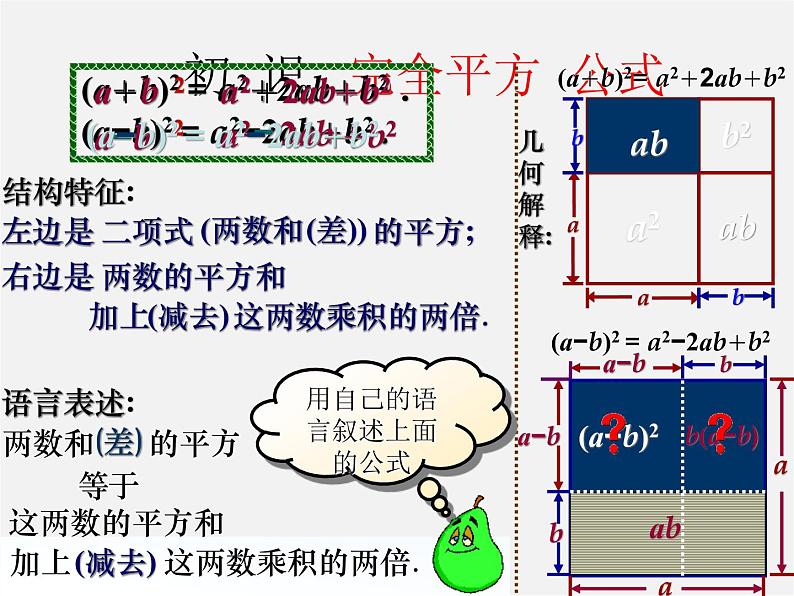
初 识 完全平方 公式
(a+b)2 = a2+2ab+b2 .(a−b)2 = a2−2ab+b2 .
a2 +b2
a2 +b2
(两数和 )
a2−2ab+b2 .
(a−b)2 = a2−2ab+b2
两数和 的平方
等于这两数的平方和
加上 这两数乘积的两倍.
例1 利用完全平方公式计算：(1) (2x−3)2 ； (2) (4x+5y)2 ; (3) (mn−a)2
使用完全平方公式与平方差公式的使用一样,
先把要计算的式子与完全平方公式对照,
明确个是 a , 哪个是 b.
(1) ( x − 2y)2 ； (2) (2xy+ x )2 ;
(3) (n +1)2 − n2.
(1) ( x − 2y)2 ； (2) (2xy+ x )2 ;
(3)(n +1)2 − n2 ;
(4) (4x + 0.5)2 ;(5) (2x2－3y2)2
2. 指出下列各式中的错误，并加以改正： (1) (2a−1)2＝2a2−2a+1; (2) (2a+1)2＝4a2 +1； (3) (a−1)2＝a2−2a−1.
利用完全平方公式计算： (1) (－1－2x)2 ； (2) (－2x+1)2
1. 注意完全平方公式和平方差公式不同：
完全平方公式的结果是三项 即 (a b)2＝a2 2ab+b2;
平方差公式的结果是两项 即 (a+b)(a−b)＝a2−b2.
2. 在解题过程中要准确确定a和b，对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2。
本节课你的收获是什么？
完全平方公式的结果 是三项， 即 (a b)2＝a2 2ab+b2;
平方差公式的结果 是两项， 即 (a+b)(a−b)＝a2−b2.
P34---35 读一读.
1、基础训练：教材p.36 习题1.13 。2、扩展训练：试一试.
纠 错 练 习
指出下列各式中的错误，并加以改正：(1) (2a−1)2＝2a2−2a+1;(2) (2a+1)2＝4a2 +1；(3) (a−1)2＝a2−2a−1.
第一数被平方时, 未添括号;
第一数与第二数乘积的2倍 少乘了一个2 ;
应改为: (2a−1)2＝ (2a)2−2•2a•1+1;
(2) 少了第一数与第二数乘积的2倍 (丢了一项);
应改为: (2a+1)2＝ (2a)2+2•2a•1 +1;
(3) 第一数平方未添括号,
第一数与第二数乘积的2倍 错了符号;
第二数的平方 这一项错了符号;
应改为: (a−1)2＝(a)2−2•(a )•1+12;