北师大版七年级下册3 探索三角形全等的条件多媒体教学ppt课件

这是一份北师大版七年级下册3 探索三角形全等的条件多媒体教学ppt课件，共24页。PPT课件主要包含了链接生活，第四章三角形，学习目标，想一想，我的知识我探索，做一做，应用格式，我的知识我应用，本节课你学到了什么等内容，欢迎下载使用。
课间，小明和小聪在操场上突然争论起来。他们都说自己比对方长得高，这时数学老师走过来，笑着对他们说：“你们不用争了，其实你们一样高，瞧瞧地上，你俩的影子一样长！”，你能运用全等三角形的有关知识说明一下其中的道理吗？（太阳光线是平行的）
探索三角形全等的条件 （二）
探索三角形全等的条件“角边角”和“角角边”.会运用“角边角”和“角角边”判别两个三角形全等.
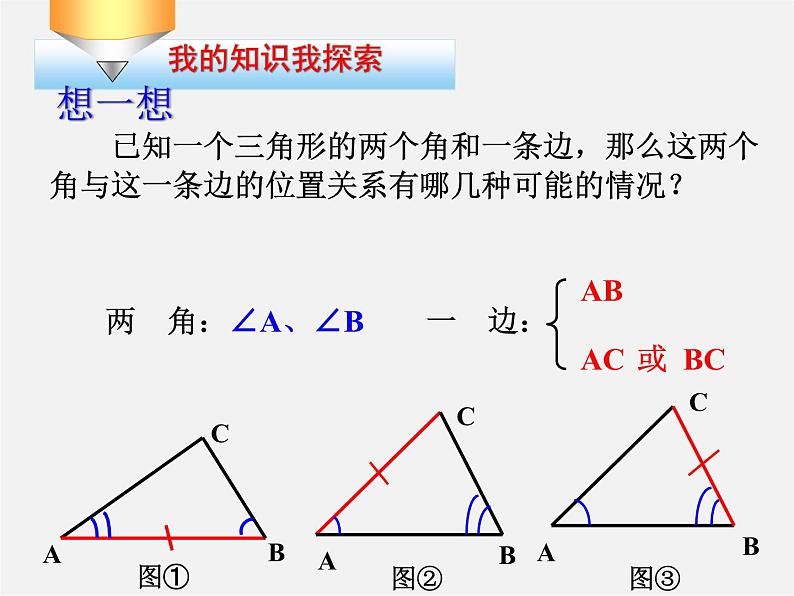
已知一个三角形的两个角和一条边，那么这两个角与这一条边的位置关系有哪几种可能的情况？
1、按要求画出三角形，并与同伴交流所画的三角形是否全等。
（1） ∠A=60°、∠B=80°、AB＝10cm（2）∠A=60°、 ∠B=45°、AB＝15cm
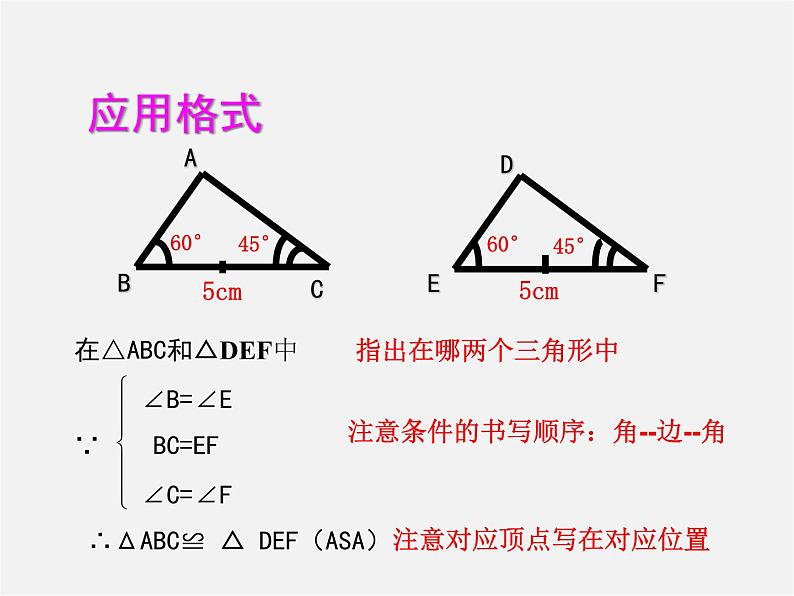
指出在哪两个三角形中
注意条件的书写顺序：角--边--角
注意对应顶点写在对应位置
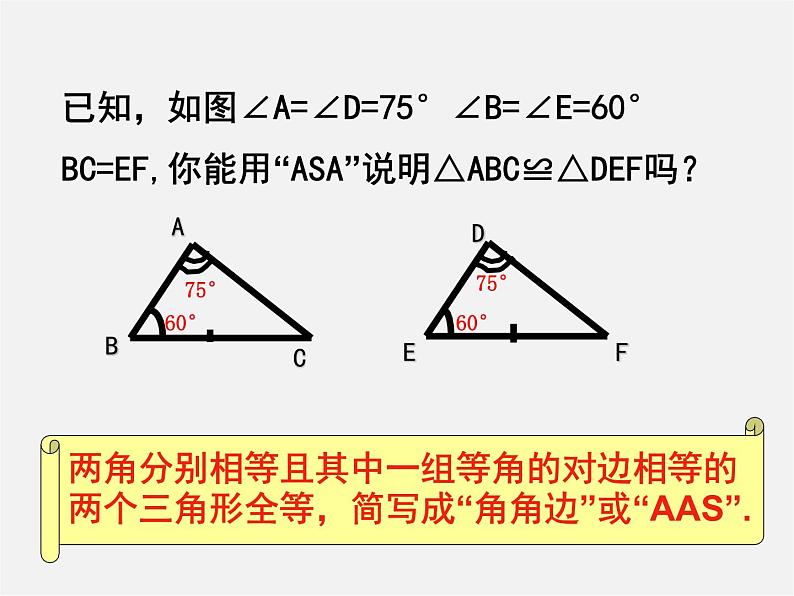
已知，如图∠A=∠D=75°∠B=∠E=60°BC=EF,你能用“ASA”说明△ABC≌△DEF吗？
注意条件的书写顺序：角--角--边
在△ABC和△DEF中 ∠B=∠E ∵ ∠A=∠D BC=EF ∴ΔABC≌△DEF（AAS）
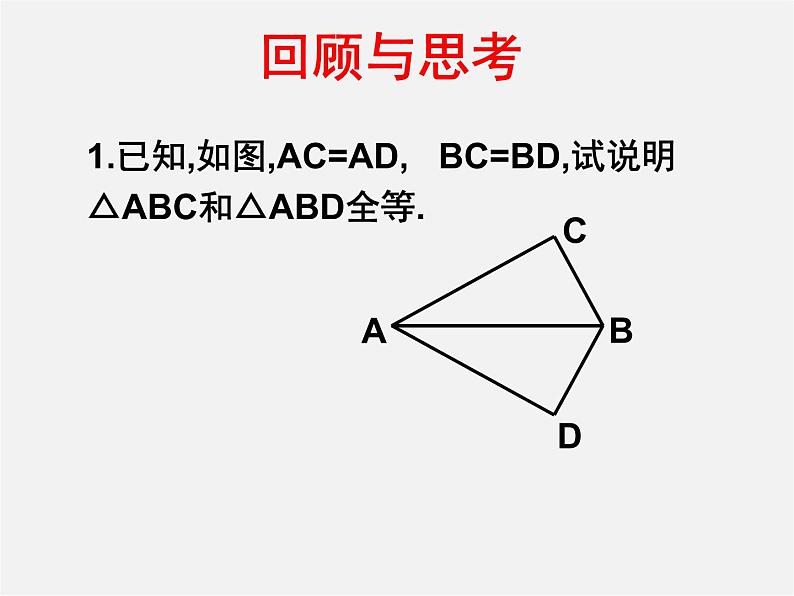
1 .如图，AB＝AC，∠B＝∠C，你能说明△ABD≌△ACE吗？
解： 在△ABD和△ACE中
∴ ≌ （ ）
如图，已知AC与BD交于点O，AD∥BC，且AD＝BC，你能说明BO=DO吗？
解：∵AD∥BC（已知）∴∠A= （ ）∠D= （ ）在 中，
∴ ≌ （ ）
两直线平行，内错角相等
在△AOD和△COB中
∠A= ∠C(已证)AD=BC (已知)∠D= ∠B (已证)
∴BO=DO（ ）
全等三角形的对应边相等
3. 如图， AB 与CD相交于点O，O是CD的中点，∠A=∠B，△AOC与△BOD全等吗？为什么？
4.课间，小明和小聪在操场上突然争论起来。他们都说自己比对方长得高，这时数学老师走过来，笑着对他们说：“你们不用争了，其实你们一样高，瞧瞧地上，你俩的影子一样长！”，你能运用全等三角形的有关知识说明一下其中的道理吗？（太阳光线是平行的）
1.两角及其夹边分别相等的两个三角形全等，简写成“角边角”或“ASA”.2.两角分别相等且其中一组等角的对边相等的两个三角形全等，简写成“角角边”或“AAS”.
说明三角形全等时要注意隐含条件的应用。
1.画图、剪切、重叠等动手操作是我们学习数学的重要方法； 2.应用分类方法可使复杂的问题明确化、简单化；3.说明线段相等或角相等时，有时可转化为说明三角形全等。
必做题：课本102页习题2.3选做题：已知，如图∠ABC= ∠DEF， ∠ACB= ∠DFE ，BE=CF，求证: AC=DF
1 .(1) 如图，已知AB=DE， ∠A =∠D， ∠B=∠E，则△ABC ≌△DEF的理由是：( )
(2)如图，已知AB=DE ,∠A=∠D，∠C=∠F，则△ABC ≌△DEF的理由是：( )
“角边角”或“ASA”
“角角边”或“AAS”
2. 图中的两个三角形全等吗? 请说明理由.
解： ΔABC≌ △DBC ，理由如下：在△ABC和△DBC中 ： ∠ABC=∠DBC (已知) ∵ ∠A=∠D（已知） BC=BC（公共边） ∴ΔABC≌ △DBC （AAS）
4.已知，如图，AB∥CD，AD∥BC，求证：AB=CD
5.已知，如图∠ABC= ∠DEF， ∠ACB= ∠DFE ，BE=CF，求证: AC=DF
证明:∵ BE=CF（已知）∴ BE+EC=CF+EC（等式性质）∴ BC=EF在△ABC和△DBC中 ： ∠ABC=∠DEF (已知)∵ BC=EF（已证） ∠ACB=∠DFE（已知）∴ΔABC≌ △DEF （ASA）∴AC=DF（全等三角形的对应边相等）
小明家的衣橱上镶有两块全等的三角形装饰玻璃，其中一块被打碎了，妈妈让小明到玻璃店配一块回来，聪明的同学，小明该怎么办？
5.已知，如图，AB∥CD，AD∥BC，试说明AB=CD