2019-2020学年某校初二（上）期末考试数学试卷 (1)

这是一份2019-2020学年某校初二（上）期末考试数学试卷 (1)，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


1. 下列图形分别是几省电视台的台徽，其中为轴对称图形的是( )
A.B.C.D.

2. 若分式x−2x+1的值为0，则x的值为（ ）
A.2或−1B.0C.2D.−1

3. 以下列各组线段长为边，不能组成三角形的是( )
A.8cm，7cm，13cmB.6cm，6cm，12cm
C.5cm，5cm，2cmD.10cm，15cm，17cm

4. 下列计算正确的是( )

A.a3⋅a3=2a3B.a32=a5
C.a5÷a3=a2D.(−2a)2=−4a2

5. 下列因式分解正确的是( )
A.x2+xy+x=xx+yB.x2−4x+4=x+2x−2
C.a2−2a+2=a−12+1D.x2−6x+5=x−5x−1

6. 如图，小明书上的三角形被墨迹遮挡了一部分，但他很快想办法在作业本画了一样的三角形，那么这两个三角形完全一样的依据是( )

A.AASB.ASAC.SSSD.SAS

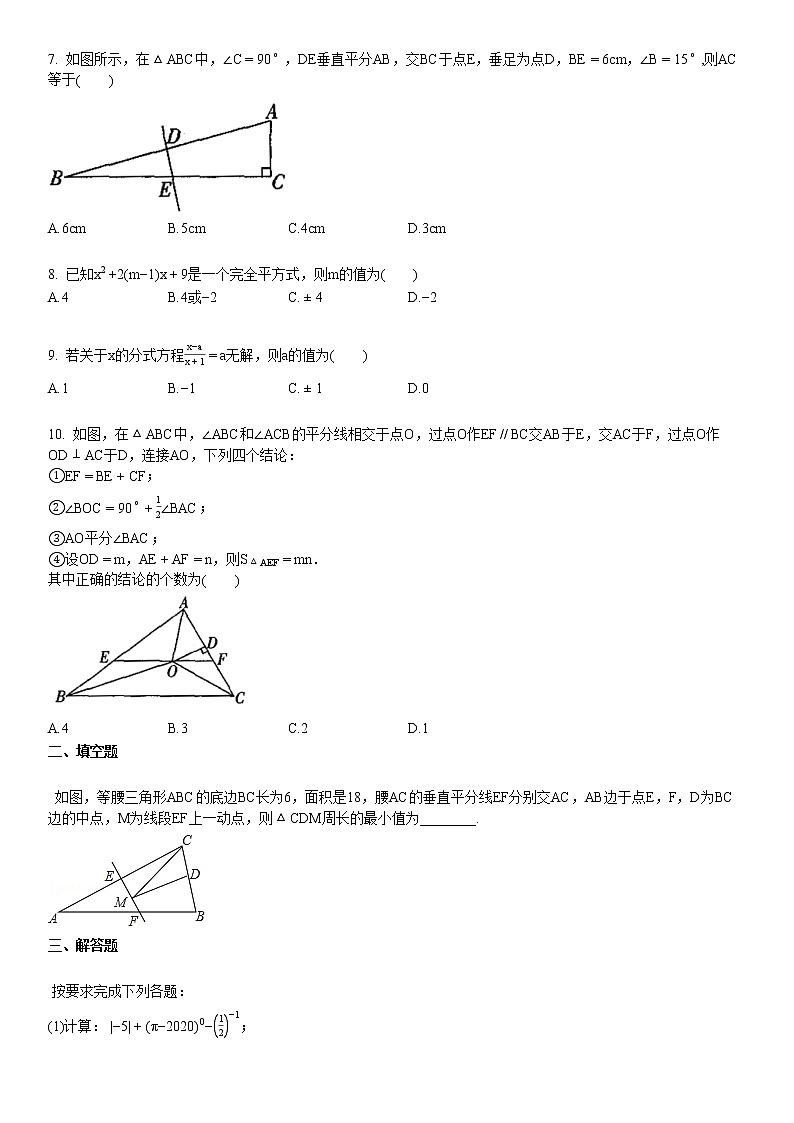
7. 如图所示，在△ABC中，∠C=90∘ ，DE垂直平分AB，交BC于点E，垂足为点D，BE=6cm，∠B=15∘ ,则AC等于( )

A.6cmB.5cmC.4cmD.3cm

8. 已知x2+2(m−1)x+9是一个完全平方式，则m的值为( )
A.4B.4或−2C.±4D.−2

9. 若关于x的分式方程x−ax+1=a无解，则a的值为( )
A.1B.−1C.±1D.0

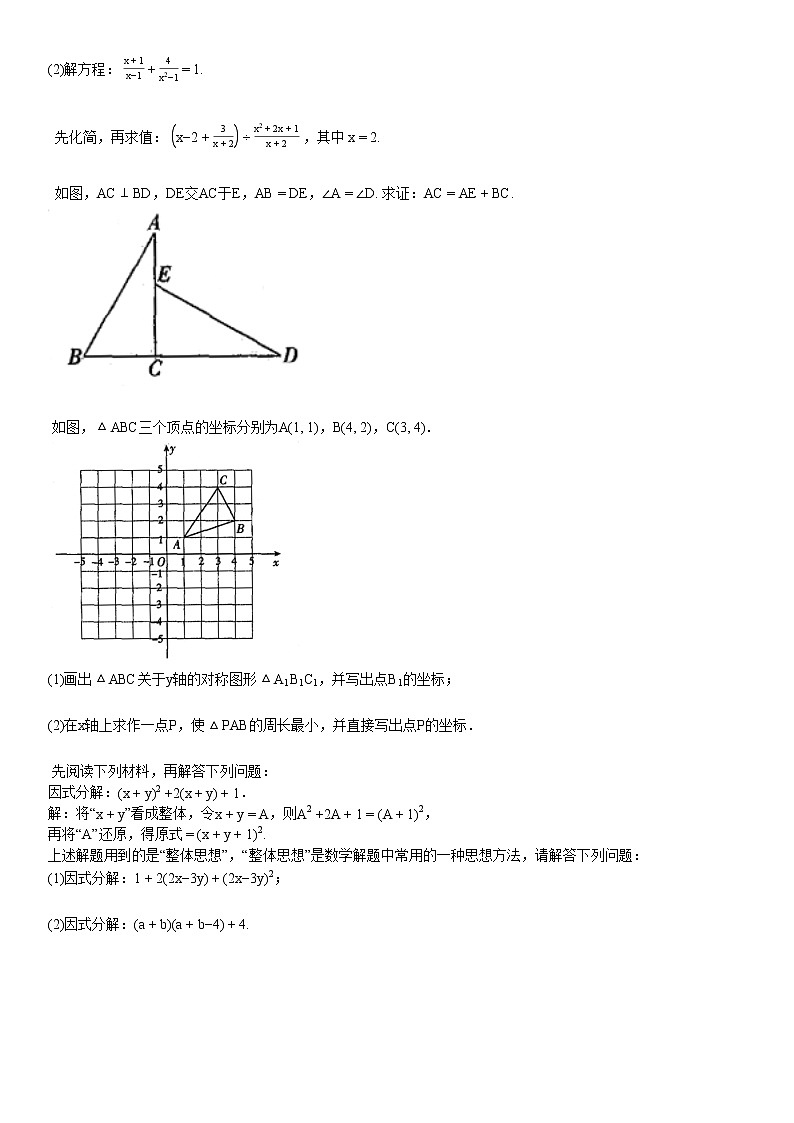
10. 如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF // BC交AB于E，交AC于F，过点O作OD⊥AC于D，连接AO，下列四个结论：
①EF=BE+CF；
②∠BOC=90∘+12∠BAC；
③AO平分∠BAC；
④设OD=m，AE+AF=n，则S△AEF=mn．
其中正确的结论的个数为( )

A.4B.3C.2D.1
二、填空题

如图，等腰三角形ABC的底边BC长为6，面积是18，腰AC的垂直平分线EF分别交AC，AB边于点E，F，D为BC边的中点，M为线段EF上一动点，则△CDM周长的最小值为________.

三、解答题

按要求完成下列各题：
(1)计算： |−5|+π−20200−12−1；

(2)解方程： x+1x−1+4x2−1=1.

先化简，再求值： x−2+3x+2÷x2+2x+1x+2 ，其中 x=2.

如图，AC⊥BD，DE交AC于E，AB=DE，∠A=∠D. 求证：AC=AE+BC.


如图，△ABC三个顶点的坐标分别为A(1, 1)，B(4, 2)，C(3, 4)．

(1)画出△ABC关于y轴的对称图形△A1B1C1，并写出点B1的坐标；

(2)在x轴上求作一点P，使△PAB的周长最小，并直接写出点P的坐标．

先阅读下列材料，再解答下列问题：
因式分解：(x+y)2+2(x+y)+1．
解：将“x+y”看成整体，令x+y=A，则A2+2A+1=(A+1)2，
再将“A”还原，得原式=(x+y+1)2.
上述解题用到的是“整体思想”，“整体思想”是数学解题中常用的一种思想方法，请解答下列问题：
(1)因式分解：1+2(2x−3y)+(2x−3y)2；

(2)因式分解：(a+b)(a+b−4)+4.

如图，在五边形ABCDE中，∠BCD=∠EDC=90∘，BC=ED，AC=AD．

(1)求证：△ABC≅△AED；

(2)若∠B=140∘，求∠BAE的度数．

某校为了创建书香校园，计划进一批图书，经了解，文学书的单价比科普书的单价少20元，用800元购进的文学书本数与用1200元购进的科普书本数相等.
(1)文学书和科普书的单价分别是多少元？

(2)该校计划用不超过5000元的费用购进一批文学书和科普书，问购进60本文学书后最多还能购进多少本科普书？

如图①，CA=CB，CD=CE，∠ACB=∠DCE=α，AD，BE相交于点M，连CM．

(1)求证：BE=AD；

(2)用含α的式子表示∠AMB的度数；

(3)当α=90∘时，分别取AD，BE的中点为P，Q，连CP，CQ，PQ，如图②，判断△CPQ的形状，并加以证明．
参考答案与试题解析
2019-2020学年湖北省孝感市某校初二（上）期末考试数学试卷
一、选择题
1.
【答案】
D
【考点】
轴对称图形
【解析】
掌握轴对称图形是解答本题的根本，需要知道两个完全一样的图形关于某条直线对折，如果两边能够完全重合，我们就说这两个图形成轴对称，这条直线就对称轴．
【解答】
解：根据轴对称图形的定义可得，
A、不是轴对称图形，故错误；
B、不是轴对称图形，故错误；
C、不是轴对称图形，故错误；
D、是轴对称图形，故正确．
故选D．
2.
【答案】
C
【考点】
分式值为零的条件
【解析】
分式的值为0的条件是：(1)分子为0；(2)分母不为0．两个条件需同时具备，缺一不可．据此可以解答本题．
【解答】
解：由题意可得：x−2=0且x+1≠0，
解得x=2．
故选C.
3.
【答案】
B
【考点】
三角形三边关系
【解析】
根据三角形两边之和大于第三边判断．
【解答】
解：A，8cm+7cm>13cm，能组成三角形；
B，6cm+6cm=12cm，不能组成三角形；
C，5cm−2cm<5cm<5cm+2cm，能组成三角形；
D，10cm+15cm>17cm，能组成三角形.
故选B.
4.
【答案】
C
【考点】
同底数幂的除法
同底数幂的乘法
【解析】
此题暂无解析
【解答】
解：A，a3⋅a3=a6，故错误；
B，a32=a6，故错误；
C，a5÷a3=a2，故正确;
D，(−2a)2=4a2，故错误.
故选C .
5.
【答案】
D
【考点】
因式分解-十字相乘法
因式分解-运用公式法
因式分解-提公因式法
【解析】
此题暂无解析
【解答】
解：x2+xy+x=xx+y+1，故A错误；
x2−4x+4=x−22，故B错误；
a2−2a+2=a−12+1，结果不是乘积的形式，故不是因式分解，故C错误；
x2−6x+5=x−5x−1，故D正确.
故选D.
6.
【答案】
B
【考点】
全等三角形的判定
【解析】
此题暂无解析
【解答】
解：根据题意，三角形的两角和它们的夹边是完整的，
所以可以利用“角边角”定理作出完全一样的三角形．
故选B．
7.
【答案】
D
【考点】
含30度角的直角三角形
线段垂直平分线的性质
【解析】
此题暂无解析
【解答】
解：连接AE，如图，
∵ 在△ABC中，∠C=90∘ ，∠B=15∘，
∴ ∠BAC=90∘−15∘=75∘，
∵ DE垂直平分AB，交BC于点E，BE=6cm，
∴ BE=AE=6cm，
∴ ∠EAB=∠B=15∘，
∴ ∠EAC=75∘−15∘=60∘，
∵ ∠C=90∘，
∴ ∠AEC=30∘，
∴ AC=12AE=12×6cm=3cm.
故选D．
8.
【答案】
B
【考点】
完全平方式
【解析】
利用完全平方公式的结构特征判断即可确定出m的值．
【解答】
解：∵ x2+2(m−1)x+9是一个完全平方式，
∴ 2(m−1)=±6，
解得：m=4或m=−2.
故选B.
9.
【答案】
C
【考点】
分式方程的解
【解析】
分式方程无解是指这个解不是分式方程的解是化简的整式方程的解，也就是使分式方程得分母为0，可以根据增根的意义列出方程，求出a的值．
【解答】
解：在方程两边同乘(x+1)得：x−a=a(x+1)，
整理得：x(1−a)=2a，
当1−a=0，即a=1时，整式方程无解，
当x+1=0，即x=−1时，分式方程无解，
把x=−1代入x(1−a)=2a得：−(1−a)=2a，
解得：a=−1.
故选C．
10.
【答案】
B
【考点】
等腰三角形的性质与判定
角平分线的性质
平行线的性质
【解析】
由在△ABC中，∠ABC和∠ACB的平分线相交于点O，根据角平分线的定义与三角形内角和定理，即可求得②∠BOC＝90∘+12∠A正确；由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出EF＝BE+CF故①正确；由角平分线的性质得出点O到△ABC各边的距离相等，故③正确；由角平分线定理与三角形面积的求解方法，即可求得③设OD＝m，AE+AF＝n，则S△AEF=12mn，故④错误．
【解答】
解：∵ 在△ABC中，∠ABC和∠ACB的平分线相交于点O，
∴ ∠OBC=∠OBE，∠OCB=∠OCF，
∵ EF // BC，
∴ ∠OBC=∠EOB，∠OCB=∠FOC，
∴ ∠EOB=∠OBE，∠FOC=∠OCF，
∴ BE=OE，CF=OF，
∴ EF=OE+OF=BE+CF，故①正确；
∵ 在△ABC中，∠ABC和∠ACB的平分线相交于点O，
∴ ∠OBC=12∠ABC，∠OCB=12∠ACB，
∠BAC+∠ABC+∠ACB=180∘，
∴ ∠OBC+∠OCB=90∘−12∠BAC，
∴ ∠BOC=180∘−(∠OBC+∠OCB)=90∘+12∠BAC，故②正确；
∵ 在△ABC中，∠ABC和∠ACB的平分线相交于点O，
∴ AO平分∠BAC，故③正确；
过点O作OM⊥AB于M，作ON⊥BC于N，
∵ 在△ABC中，∠ABC和∠ACB的平分线相交于点O，
∴ ON=OD=OM=m，
∴ S△AEF=S△AOE+S△AOF=12AE⋅OM+12AF⋅OD
=12OD⋅(AE+AF)=12mn，故④错误.
故选B.
二、填空题
【答案】
9
【考点】
轴对称——最短路线问题
线段垂直平分线的性质
【解析】
连接AD，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再再根据EF是线段AC的垂直平分线可知，点C关于直线EF的对称点为点A，故AD的长为CM+MD的最小值，由此即可得出结论．
【解答】
解：连接AD，如图.
∵ △ABC是等腰三角形，点D是BC边的中点，
∴ AD⊥BC，
∴ S△ABC=12BC⋅AD=12×6×AD=18，解得AD=6.
∵ EF是线段AC的垂直平分线，
∴ 点C关于直线EF的对称点为点A，
∴ AD的长为CM+MD的最小值，
∴ △CDM最小的周长=(CM+MD)+CD
=AD+12BC=6+12×6
=6+3=9．
故答案为：9.
三、解答题
【答案】
解：(1)原式=5+1−2=4；
(2)方程两边乘以 x+1x−1得，
x+12+4=x+1x−1，
解得：x=−3，
检验：当x=−3时，x+1x−1≠0，
∴ x=−3是原方程的解，
∴ 原方程的解是：x=−3.
【考点】
零指数幂、负整数指数幂
解分式方程
绝对值
【解析】
此题暂无解析
【解答】
解：(1)原式=5+1−2=4；
(2)方程两边乘以 x+1x−1得，
x+12+4=x+1x−1，
解得：x=−3，
检验：当x=−3时，x+1x−1≠0，
∴ x=−3是原方程的解，
∴ 原方程的解是：x=−3.
【答案】
解：原式 =x2−4+3x+2⋅x+2x2+2x+1
=x+1x−1x+2⋅x+2x+12
=x−1x+1，
当x=2时，原式=2−12+1=13.
【考点】
分式的化简求值
【解析】
此题暂无解析
【解答】
解：原式 =x2−4+3x+2⋅x+2x2+2x+1
=x+1x−1x+2⋅x+2x+12
=x−1x+1，
当x=2时，原式=2−12+1=13.
【答案】
证明：∵ AC⊥BD，
∴ ∠ACB=∠DCE=90∘.
在△ABC和△DEC中，
∠A=∠D,∠ACB=∠DCE,AB=DE,
∴ △ABC≅△DECAAS，
∴BC=EC.
∵AC=AE+EC，
∴AC=AE+BC.
【考点】
全等三角形的性质与判定
【解析】
此题暂无解析
【解答】
证明：∵ AC⊥BD，
∴ ∠ACB=∠DCE=90∘.
在△ABC和△DEC中，
∠A=∠D,∠ACB=∠DCE,AB=DE,
∴ △ABC≅△DECAAS，
∴BC=EC.
∵AC=AE+EC，
∴AC=AE+BC.
【答案】
解：(1)如图所示，△A1B1C1即为所求；
点B1的坐标为(−4,2);
(2)如图，过x轴作A的对称点为A′，连接A′B,
则A′B与x轴的交点即为所求点P的位置，
故点P坐标为(2,0).
【考点】
轴对称——最短路线问题
作图-轴对称变换
【解析】
（1）根据轴对称的性质进行作图，即可得到△ABC关于y轴的对称图形△A1B1C1；
【解答】
解：(1)如图所示，△A1B1C1即为所求；
点B1的坐标为(−4,2);
(2)如图，过x轴作A的对称点为A′，连接A′B,
则A′B与x轴的交点即为所求点P的位置，
故点P坐标为(2,0).
【答案】
解：(1)将”2x−3y“看作一个整体，令2x−3y=A,
则1+2A+A2=(A+1)2，
再将“A”还原，得原式=(2x−3y+1)2;
(2)将“a+b”看作一个整体，令a+b=A，
则A(A−4)+4=A2−4A+4=(A−2)2，
再将“A”还原，
得原式=(a+b−2)2.
【考点】
因式分解的应用
完全平方公式
【解析】
（1）把(x−y)看作一个整体，直接利用完全平方公式因式分解即可；
（2）令A=a+b，代入后因式分解后代入即可将原式因式分解；
【解答】
解：(1)将”2x−3y“看作一个整体，令2x−3y=A,
则1+2A+A2=(A+1)2，
再将“A”还原，得原式=(2x−3y+1)2;
(2)将“a+b”看作一个整体，令a+b=A，
则A(A−4)+4=A2−4A+4=(A−2)2，
再将“A”还原，
得原式=(a+b−2)2.
【答案】
(1)证明：∵ AC=AD，
∴ ∠ACD=∠ADC.
又∵ ∠BCD=∠EDC=90∘，
∴ ∠ACB=∠ADE.
在△ABC和△AED中，
BC=ED,∠ACB=∠ADE,AC=AD,
∴ △ABC≅△AED(SAS)；
(2)∵ △ABC≅△AED，
∴ 当∠B=140∘时，∠E=140∘.
又∵ ∠BCD=∠EDC=90∘，
∴ 五边形ABCDE中，∠BAE=540∘−140∘×2−90∘×2=80∘．
【考点】
多边形的内角和
全等三角形的判定
全等三角形的性质
【解析】
（1）根据∠ACD=∠ADC，∠BCD=∠EDC=90∘，可得∠ACB=∠ADE，进而运用SAS即可判定全等三角形；
（2）根据全等三角形对应角相等，运用五边形内角和，即可得到∠BAE的度数．
【解答】
(1)证明：∵ AC=AD，
∴ ∠ACD=∠ADC.
又∵ ∠BCD=∠EDC=90∘，
∴ ∠ACB=∠ADE.
在△ABC和△AED中，
BC=ED,∠ACB=∠ADE,AC=AD,
∴ △ABC≅△AED(SAS)；
(2)∵ △ABC≅△AED，
∴ 当∠B=140∘时，∠E=140∘.
又∵ ∠BCD=∠EDC=90∘，
∴ 五边形ABCDE中，∠BAE=540∘−140∘×2−90∘×2=80∘．
【答案】
解：(1)设文字书的单价为x元/本，
则科普书的单价为x+20元/本，依题意得，
800x=1200x+20，
解得：x=40，
经检验， x=40是原分式方程的解，且符合题意，
答：文学书的单价是40元/本，科普书的单位为60元/本；
(2)设购进m本科普书，依题意得：
40×60+60m≤5000，
解得：m≤4313，
∵ m是整数，
∴ m的最大值为43.
答：购进60本文学书后最多还能购进43本科普书.
【考点】
一元一次不等式的实际应用
分式方程的应用
【解析】
此题暂无解析
【解答】
解：(1)设文字书的单价为x元/本，
则科普书的单价为x+20元/本，依题意得，
800x=1200x+20，
解得：x=40，
经检验， x=40是原分式方程的解，且符合题意，
答：文学书的单价是40元/本，科普书的单位为60元/本；
(2)设购进m本科普书，依题意得：
40×60+60m≤5000，
解得：m≤4313，
∵ m是整数，
∴ m的最大值为43.
答：购进60本文学书后最多还能购进43本科普书.
【答案】
(1)证明：∵ ∠ACB=∠DCE=α，
∴ ∠ACD=∠BCE.
在△ACD和△BCE中，
CA=CB，∠ACD=∠BCE，CD=CE，
∴ △ACD≅△BCE(SAS)，
∴ BE=AD；
(2)解：∵ △ACD≅△BCE，
∴ ∠CAD=∠CBE，
∵ 在△ABC中，
∠BAC+∠ABC=180∘−α，
∴ ∠BAM+∠ABM=180∘−α，
∴ 在△ABM中，
∠AMB=180∘−(180∘−α)=α；
(3)△CPQ为等腰直角三角形．
证明：由(1)可得，BE=AD，
∵ AD，BE的中点分别为点P，Q，
∴ AP=BQ.
∵ △ACD≅△BCE，
∴ ∠CAP=∠CBQ.
在△ACP和△BCQ中，
CA=CB,∠CAP=∠CBQ,AP=BQ,
∴ △ACP≅△BCQ(SAS)，
∴ CP=CQ，且∠ACP=∠BCQ.
又∵ ∠ACP+∠PCB=90∘，
∴ ∠BCQ+∠PCB=90∘，
∴ ∠PCQ=90∘，
∴ △CPQ为等腰直角三角形．
【考点】
全等三角形的性质与判定
三角形综合题
三角形内角和定理
等腰直角三角形
全等三角形的性质
【解析】
（1）由CA=CB，CD=CE，∠ACB=∠DCE=α，利用SAS即可判定△ACD≅△BCE；
（2）根据△ACD≅△BCE，得出∠CAD=∠CBE，再根据∠AFC=∠BFH，即可得到∠AMB=∠ACB=α；
（3）先根据SAS判定△ACP≅△BCQ，再根据全等三角形的性质，得出CP=CQ，∠ACP=∠BCQ，最后根据∠ACB=90∘即可得到∠PCQ=90∘，进而得到△PCQ为等腰直角三角形．
【解答】
(1)证明：∵ ∠ACB=∠DCE=α，
∴ ∠ACD=∠BCE.
在△ACD和△BCE中，
CA=CB，∠ACD=∠BCE，CD=CE，
∴ △ACD≅△BCE(SAS)，
∴ BE=AD；
(2)解：∵ △ACD≅△BCE，
∴ ∠CAD=∠CBE，
∵ 在△ABC中，
∠BAC+∠ABC=180∘−α，
∴ ∠BAM+∠ABM=180∘−α，
∴ 在△ABM中，
∠AMB=180∘−(180∘−α)=α；
(3)△CPQ为等腰直角三角形．
证明：由(1)可得，BE=AD，
∵ AD，BE的中点分别为点P，Q，
∴ AP=BQ.
∵ △ACD≅△BCE，
∴ ∠CAP=∠CBQ.
在△ACP和△BCQ中，
CA=CB,∠CAP=∠CBQ,AP=BQ,
∴ △ACP≅△BCQ(SAS)，
∴ CP=CQ，且∠ACP=∠BCQ.
又∵ ∠ACP+∠PCB=90∘，
∴ ∠BCQ+∠PCB=90∘，
∴ ∠PCQ=90∘，
∴ △CPQ为等腰直角三角形．