数学七年级下册第二章 相交线与平行线2 探索直线平行的条件教案设计

这是一份数学七年级下册第二章 相交线与平行线2 探索直线平行的条件教案设计，共6页。教案主要包含了教学目标，教学重点，教学难点，教学过程等内容，欢迎下载使用。
《2.2 探索直线平行的条件》一、教学目标（一）教学知识点1.会判断内错角、同旁内角.2.直线平行的条件.（二）能力训练要求1.经历观察、操作、想象、推理、交流等活动，进一步发展空间观念、推理能力和有条理表达的能力.2.经历探索直线平行的条件的过程，掌握直线平行的条件，并能解决一些实际问题.（三）情感与价值观要求创设情境，激发学生积极参与交流、学习，主动解决问题，鼓励其创造精神，并从中使他们受益.二、教学重点两条直线平行的条件：角相等或互补.三、教学难点两条直线平行的条件的应用.四、教学过程Ⅰ.创设现实情景，引入新课［师］上节课我们探讨了直线平行的条件.谁来给大家总结一下：判定两条直线平行的方法.［生］判定两条直线平行的方法到现在为止有以下三种：①定义：即：在同一平面内不相交的两条直线是平行线.②如果两条直线都与第三条直线平行，那么这两条直线互相平行.③同位角相等，两直线平行.［师］这位同学总结得很好.大家要会应用这些方法来判定两直线平行.下面来看一个实际例子小明有一块小画板，他想知道它的上下边缘是否平行，于是他在两个边缘之间画了一条线段AB.（如图2－23所示）图2－23小明身边只有一个量角器，他通过测量某些角的大小就能知道这个画板的上下边缘是否平行，你知道他是怎样做的吗？［师］大家分组讨论一下.［生甲］小明只有量角器，所以想到应该用“同位角相等，两直线平行”来判定.但图中又没有同位角，是不是应该找另外的角呢？
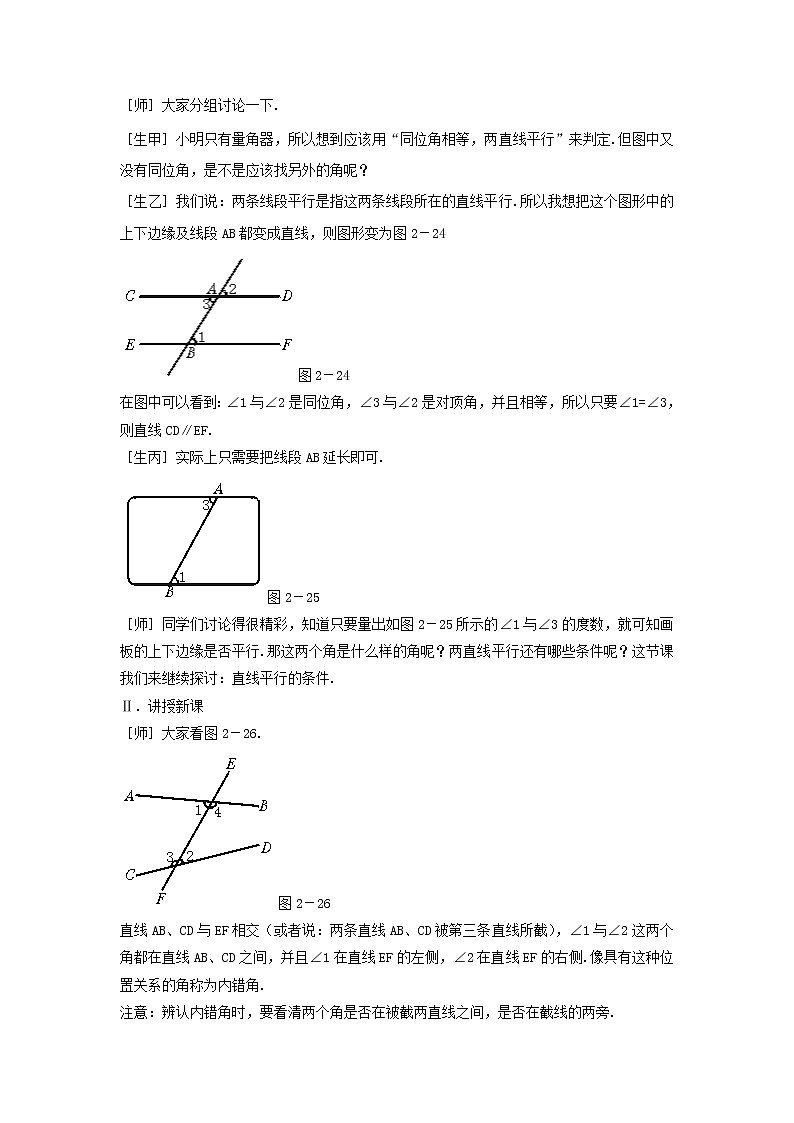
［生乙］我们说：两条线段平行是指这两条线段所在的直线平行.所以我想把这个图形中的上下边缘及线段AB都变成直线，则图形变为图2－24图2－24在图中可以看到：∠1与∠2是同位角，∠3与∠2是对顶角，并且相等，所以只要∠1=∠3，则直线CD∥EF.［生丙］实际上只需要把线段AB延长即可.图2－25［师］同学们讨论得很精彩，知道只要量出如图2－25所示的∠1与∠3的度数，就可知画板的上下边缘是否平行.那这两个角是什么样的角呢？两直线平行还有哪些条件呢？这节课我们来继续探讨：直线平行的条件.Ⅱ．讲授新课［师］大家看图2－26.图2－26直线AB、CD与EF相交（或者说：两条直线AB、CD被第三条直线所截），∠1与∠2这两个角都在直线AB、CD之间，并且∠1在直线EF的左侧，∠2在直线EF的右侧.像具有这种位置关系的角称为内错角.注意：辨认内错角时，要看清两个角是否在被截两直线之间，是否在截线的两旁.［师］图中还有内错角吗？［生］有，∠3与∠4是内错角.［师］好，我们再看：∠1与∠3的位置关系如何呢？［生］∠1与∠3，这两个角也都在直线AB、CD之间，但它们在直线EF的同一旁.［师］同学们说得很好，我们把具有这种位置关系的角称为同旁内角.［生甲］老师，我知道了，那么∠2与∠4也是同旁同角，是吧？［师］对，那谁能说一说：辨认同旁内角要掌握什么呢？［生乙］要看清两个角是否在截线的同旁，是否在被截两直线之间.［师］很好，下面同学们看图，从中找出同位角、内错角、同旁内角.辨认时，一定要注意哪两条直线被哪一条直线所截.在下图中，找出所有的同位角、内错角、同旁内角.图2－27［生甲］∠1与∠2、∠3与∠4、∠5与∠6是同位角.∠4与∠6是内错角.∠4与∠2是同旁内角.［生乙］还有呢：∠7与∠8是同位角，∠2与∠8是内错角，∠6与∠8是同旁内角.［师］还有吗？［生齐声］没有了.［师］好.两条直线被第三条直线所截，形成了八个角，这八个角之间的关系要弄清楚.现在我们再来看那个实例——小明测画板上下边缘是否平行.刚才我们经过讨论得知：当∠1=∠3时画板的上下边缘就平行.那么∠1与∠3是什么角呢？由此可得出什么结论呢？［生］∠1与∠3是内错角.由此可得出：内错角相等，两条直线就平行.［师］很好.由此我们又得出了直线平行的条件，或者说是判定两条直线平行的方法：内错角相等，两直线平行.同学们来叙述一下为什么.［生］如图2－28，∠3与∠2是对顶角，相等，又由于∠1=∠3，所以∠2=∠1，因此可以得出AB∥CD.图2－28［师］同学们叙述得很好，即：AB∥CD（内错角相等，两直线平行）［师］三线八角中，我们能用同位角相等或内错角相等来判定两条直线平行，那同旁内角又如何呢？下面大家来议一议：同旁内角满足什么关系时，两条直线平行？为什么？（分组讨论、归纳）［生甲］如图2－29，当∠1=∠2时，AB∥CD，而∠1+∠5=180°.图2－29所以猜想∠2+∠5=180°时，AB∥CD.验证：当∠2+∠5=180°时，又∠1+∠5=180°（平角定义），所以由“同角的补角相等”，可得：∠1=∠2，因此由“同位角相等，两直线平行”可得：AB∥CD.从而可知：同旁内角互补，两直线平行.［生乙］还可以这样验证：当∠2+∠5=180°时，又平角定义可知：∠3+∠5=180°，所以可得出：∠3=∠2，∠3与∠2是内错角，因此可由“内错角相等，两直线平行”得出：AB∥CD.［师］很好.由此我们可得出什么结论？［生齐声］同旁内角互补，两直线平行.［师］很好.应用这个判定时可这样书写：∠2+∠5=180°→AB∥CD.接下来，我们来做一做.如图2－30，三个相同的三角尺拼接成一个图形.请找出图中的一组平行线，并说明你的理由.图2－30小华：AC与DE是平行的，因为∠EDC与∠ACB是同位角，而且又相等.你能看懂她的意思吗？小明：我是这样想的：∠BCA=∠EAC→BD∥AE.你知道这一步的理由吗？（学生动手操作，叙述后，再出示小明、小华的想法.）［生甲］通过摆放，可知：∠CBA=∠DCE，而这两个角是同位角，所以BA∥CE.［生乙］通过摆放，可知：∠B+∠BAE=180°，而∠B与∠BAE是同旁内角，所以BD∥AE.［生丙］因为∠ACE与∠CED是内错角，且相等，所以AC∥DE.……（学生用自己的语言来叙述理由，课堂气氛活跃.）［师］同学们叙述得真好，下面看一看小华与小明的理由，你们能看懂吗？［生齐声］能.［师］好，通过做一做，我们熟悉了直线平行的条件.在今后的学习中，要能够直接应用.接下来同学们做练习以巩固所学内容.Ⅲ．课堂练习1.观察图2－31并填空.图2－31（1）∠1与       是同位角.（2）∠5与       是同旁内角.（3）∠2与       是内错角.答案：（1）∠4  （2）∠3  （3）∠12.当图2－32中各角分别满足下列条件时，你能指出哪两条直线平行吗？图2－32（1）∠1=∠4，（2）∠2=∠4，（3）∠1+∠3=180°答案：（1）∠1=∠4→a∥b（2）∠2=∠4→m∥l（3）∠1+∠3=180°→n∥lⅣ．课时小结本节课我们又探讨了直线平行的条件.到现在为止，我们学习了以下五种判定两直线平行的方法：（1）定义（不常用）.（2）如果两直线都和第三条直线平行，那么这两条直线互相平行.（3）同位角相等，两直线平行.（4）内错角相等，两直线平行.（5）同旁内角互补，两直线平行.大家要注意结合已知条件选用适当的判定方法来判定两直线平行.Ⅴ．课后作业