初中数学3 平行线的判定课堂教学课件ppt

这是一份初中数学3 平行线的判定课堂教学课件ppt，共18页。PPT课件主要包含了平角的定义，等量代换，互补的意义，等式的性质，垂直的性质，∠EBA，∠BAD，ABCD，平角180º，ABC等内容，欢迎下载使用。

公理：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.简单说成：同位角相等，两直线平行.
如图，直线AB、CD被直线EF所截，图中哪些角是同位角？哪些角是内错角？哪些角是同旁内角？
1.知识目标 （1）使学生掌握平行线的判定方法． （2）能运用所学过的平行线的判定方法，进行简单的推理和计算．2.教学重点 平行线的判定方法的发现、说理和应用．3.教学难点 问题的思考和推理过程是难点．
已知: 如图,∠1和∠2是直线a,b被直线c 截出的同旁内角,且∠1与∠2互补.求证: a∥b.
证明: ∵ ∠1与∠2互补,
∴∠1+∠2=1800.
∴∠1= 1800 －∠2 ,
又∵∠3+∠2=180° ,
∴∠3= 1800 －∠2.
∴∠1=∠3 ,
∴ a∥b.
证明一个真命题的方法,步骤,书写格式以及注意事项.
公理,定义和已经证明的定理都可以作为依据,用来证明新的定理.
(同位角相等,两直线平行)
定理 : 两条直线被第三条直线所截,如果同旁内角互补,那么这两 条直线平行.
已知: 如图,∠1和∠2是直线a,b被直线c 截出的内错角,且∠1=∠2.求证: a∥b.
证明:∵ ∠1=∠2 ,
∠1+∠3=1800 ,
∴∠2+∠3 = 1800 ,
∴∠2与∠3互补 ,
∴ a∥b .
定理 两条直线被第三条直线所截,如果内错角相等, 那么这两条直线平行. 内错角相等,两直线平行.
(同旁内角互补,两直线平行)
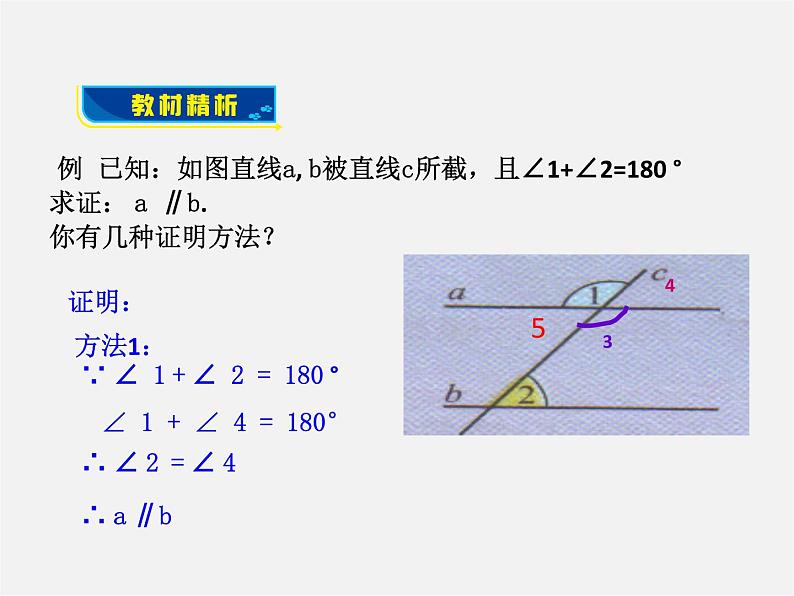
例 已知：如图直线a, b被直线c所截，且∠1+∠2=180 °求证： a ∥b.你有几种证明方法？
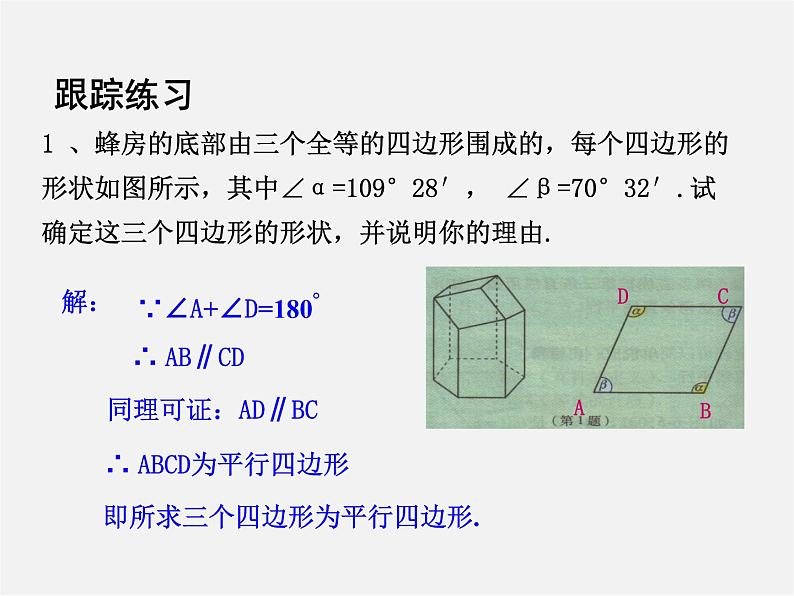
1 、蜂房的底部由三个全等的四边形围成的，每个四边形的形状如图所示，其中∠α=109°28′， ∠β=70°32′.试确定这三个四边形的形状，并说明你的理由.
内错角相等，两直线平行
同旁内角互补，两直线平行
平行于同一条直线的两条直线互相平行
2.完成下列推理，并在括号中写出相应的根据.
3.如图：直线AB,CD都和AE相交，∠1+∠A=180° 求证：AB//CD
（ ）
证明：∵∠1+∠3=180 º（平角=180º） ∠2+∠3=180 º（
4.如果两条直线都和第三条直线垂直，那么这两条直线平行
已知，如图，直线a⊥c,b⊥c.求证：a∥b. 证明：∵a⊥c,b⊥c（已知）∴∠1=90°∠2=90°（垂直的定义）∴∠1=∠2（等量代换）∴b∥a（同位角相等，两直线平行）
如图BE平分∠ABC，EC平分∠ BCD， ∠ E=90°那么AB∥CD吗？为什么？
解：∵BE 平分∠ABC（已知）∴∠___ =2∠1∵EC平分∠BCD（已知）∴∠____ =2∠2∵∠E+∠1+∠2=180°∴∠1+∠2=___°-∠E∵∠E =90°（已知）∴∠1+∠2=_ °∴∠ABC +∠BCD =2∠_+2∠_=___°∴_____ （ ）
AB∥CD 同旁内角互补，两直线平行
1.如图， ∠ D=∠EFC，那么（ ）A．AD∥BC B．AB∥CD C．EF∥BC D．AD∥EF2.如图，判定AB∥CE的理由是（ ）A．∠B=∠ACE B．∠A=∠ECD C．∠B=∠ACB D．∠A=∠ACE3.如图，下列推理正确的是（ ）A．∵∠1=∠3，∴ a∥ b B．∵∠1=∠2，∴a ∥b C．∵∠1=∠2，∴c ∥ d D．∵∠1=∠3，∴ c∥ d
4．已知：如图，CE平分∠ACD，∠1=∠B，求证：AB∥CE
5.如图：∠1=53 º，∠2= 127º，∠3= 53º，试说明直线AB与CD，BC与DE的位置关系.
证明： ∵ CE平分∠ACD， ∴∠1=∠2，∵∠1=∠B，∴∠ B =∠2，∴AB∥CE
证明： ∵ ∠2= 127º，∴ ∠4=180º-127º=53º,∵ ∠3= 53º∴∠3=∠4，∴AB∥CD.∵∠1=∠3，∴BC∥DE
同旁内角互补两直线平行