北师大版八年级下册1 因式分解图文课件ppt

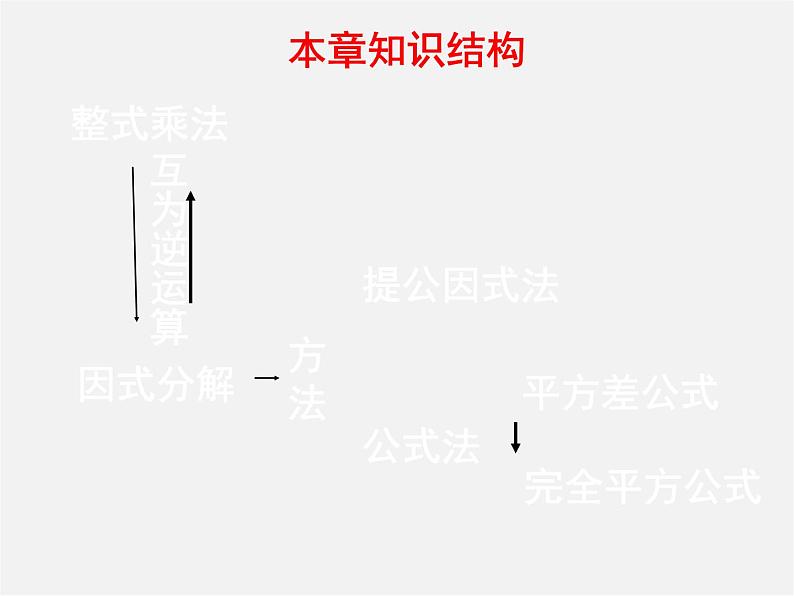
这是一份北师大版八年级下册1 因式分解图文课件ppt，共22页。PPT课件主要包含了因式分解，提公因式法，公式法，整式乘法，互为逆运算，平方差公式，完全平方公式，本章知识结构，多项式，小结与反思等内容，欢迎下载使用。
一般地，把一个多项式表示成几个整式的乘积的形式，称为把这个多项式因式分解，有时我们也把这一过程叫做分解因式。
要求： 1.变形对象：是 ;　　　 2.变形过程：由 变成 的形式　　　 3.变形的结果：是几个 的积 4.分解结果中的每个因式不能再分
只有多项式才可能进行因式分解
1、确定公因式的方法：
2、提公因式法分解因式：
第一步，找出公因式；第二步，提公因式（ 把多项式化为两个因式的乘积）
1)定系数 2)定字母 3)定指数
1、两个多项式的各项都互为相反数，则这两个多项式也互为相反数。
如：(1) a-b 与 b-a 互为相反数.
(2) a+b 与 -a-b 互为相反数.
2、互为相反数的项，它们的偶次幂相等，奇次幂互为相反数。即若
(3) a-b+c 与 ( ) 互为相反数.
3、两个多项式的各项都相同时，则这两个多项式也相等。
如: a-b 和 -b+a 即 a-b = -b+a
如果把乘法公式反过来，那么就可以用来把某些多项式分解因式，这种分解因式的方法叫做运用公式法。
公式法的概念
观察多项式x2-25，9x2-y2，完成以下探究问题，并与同伴交流．
1．两个多项式的共同特征:多项式都只有 项，项的符号 ，每一项都可以写成 的形式．
x2-25= 2 - 2 = ( )( )；
9x2-y2= 2 - 2 =( )( ) ．
2．尝试将x2-25，9x2-y2写成两个因式的乘积：
依据是： ．
a2-b2=(a+b)(a-b)
2、有两个平方的“项”
3、有这两平方“项”底数的2倍或-2倍
知识点一：对因式分解概念的理解
例1.下列式子从左到右的变形中是分解因式的为（ ）。 A. B. C. D.
知识点二：利用提公因式法分解因式
例2.把下列各式分解因式⑴ ⑵解：原式
公因式既可以是单项式，也可以是多项式，需要整体把握。
例3.把下列各式分解因式 ⑴ 解：原式 ⑵解：原式
知识点三：利用公式法分解因式
⑶ 解：原式⑷解：原式
练一练：把下列各式分解因式 ⑴解：原式 ⑵ 解：原式
当多项式形式上是二项式时，应考虑用平方差公式，当多项式形式上是三项式时，应考虑用完全平方公式。
例4.把下列各式分解因式 ⑴ 解：原式 ⑵ 解：原式
知识点四：综合运用多种方法分解因式
⑶解：原式 ⑷解：原式
先观察是否有公因式，若有公因式提出后看是否具有平方差公式或完全平方公式特征，若有使用公式法；若都没有，则考虑将多项式进行重新整理或分组后进行分解因式。
知识点五：运用分解因式进行计算和求值
例5.利用分解因式计算 ⑴解：原式
⑵ 解：原式 ⑶ 解：原式
例6.已知 ,求 的值。 解：
例7.已知 ，求 的值。 解：
知识点六：分解因式的实际应用
例9.如图，在一个半径为R的圆形钢板上，机械加工时冲去半径为r的四个小圆． （1）用代数式表示剩余部分的面积； （2）用简便方法计算：当R=7.5，r=1.25时，剩余部分的面积．
(2)当R=7.5，r=1.25时， S=πR2 –4πr2 =π(R+2r)(R –2r) =π(7.5+2×1.25)(7.5 –2×1.25) =π×10×5=50π
解：(1)S=πR2 –4πr2