初中数学北师大版八年级下册1 平行四边形的性质教学演示ppt课件

这是一份初中数学北师大版八年级下册1 平行四边形的性质教学演示ppt课件，共22页。PPT课件主要包含了平行四边形特征的探索，体验感知，探索归纳交流合作，平行四边形性质的探索，推理论证感悟升华，应用巩固深化提高，评价反思概括总结等内容，欢迎下载使用。

第六章 平行四边形 6.1 平行四边形的性质(一)
做一做 :小组活动1： 请同学制作两个全等的三角形。
想一想: 观察两个全等的三角形，将它们相等的一组边重合，得到一个怎样的四边形？对边有什么特征？
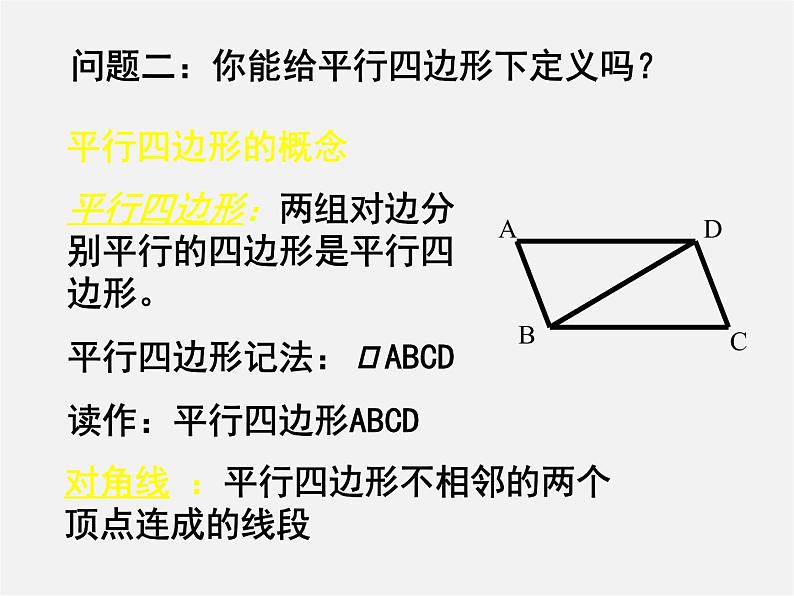
问题二：你能给平行四边形下定义吗？
对角线 ：平行四边形不相邻的两个顶点连成的线段
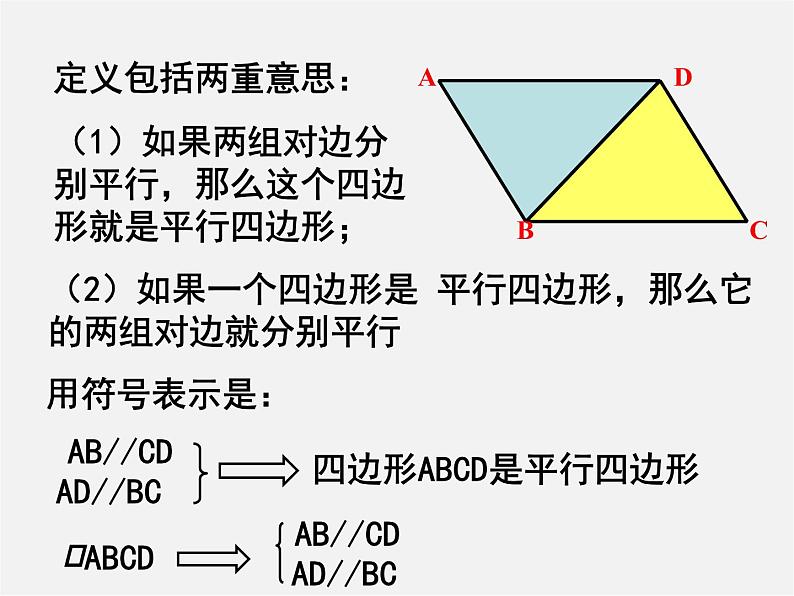
定义包括两重意思：（1）如果两组对边分别平行，那么这个四边形就是平行四边形；
（2）如果一个四边形是 平行四边形，那么它的两组对边就分别平行
四边形ABCD是平行四边形
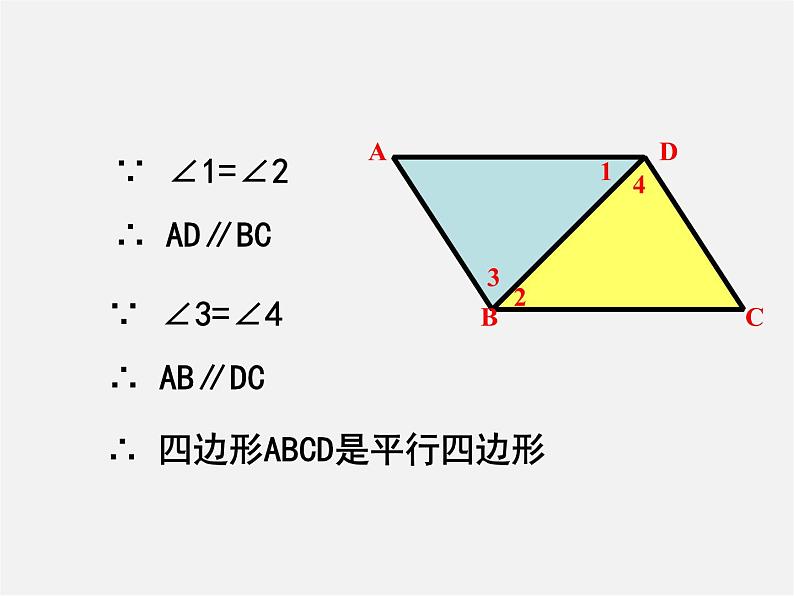
∵ ∠1=∠2 ∴ AD∥BC
∵ ∠3=∠4 ∴ AB∥DC
∴ 四边形ABCD是平行四边形
生活中常见到那些平行四边形的实例,你能举出几个吗?
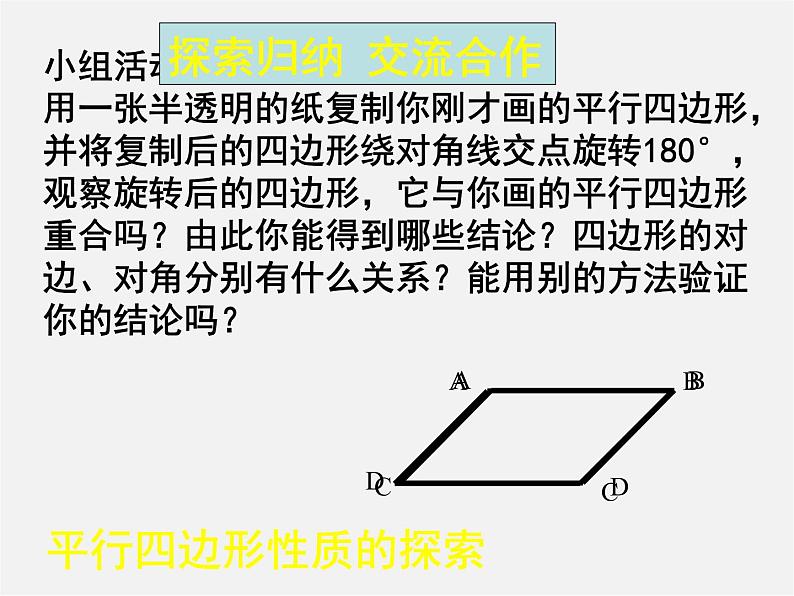
小组活动3用一张半透明的纸复制你刚才画的平行四边形，并将复制后的四边形绕对角线交点旋转180°，观察旋转后的四边形，它与你画的平行四边形重合吗？由此你能得到哪些结论？四边形的对边、对角分别有什么关系？能用别的方法验证你的结论吗？
结论1：平行四边形是中心对称图形，两条对角线的交点是他的对称中心
结论：平行四边形的对边平行且相等。
平行四边形的对角相等。
∵ 四边形ABCD是平行四边形∴ AB=DC , AD=BC. ∠A=∠C , ∠B=∠D.∴ AB∥DC, AD∥BC
问题四：平行四边形的对边、对角分别有 什么关系？
问题四： 平行四边形的性质： 平行四边形的对边相等 平行四边形的对角相等能用别的方法验证你的结论吗？
可以通过推理来证明这个结论：
例：如图6-2（1），四边形ABCD是平行四边形. 求证:AB=CD,BC=DA.
证明:如图6-2(2),连接AC.∵ 四边形ABCD是平行四边形∴ AD // BC，AB // CD ∴ ∠1=∠2，∠3=∠4∴ △ABC和△CDA中 ∠2=∠1 AC=CA ∠3=∠4∴ △ABC≌△CDA（ASA）∴ AB=DC， AD=CB
你能证明平行四边形的对角相等吗？
如图6-2（1），四边形ABCD是平行四边形.求证: ∠A=∠C,∠B=∠D.
证明:如图6-2(2),连接AC.∵ 四边形ABCD是平行四边形∴ AD // BC， AB // CD ∴ ∠A+∠B=180 ° ∠A+∠D=180 °∴ ∠B=∠D同理可得：∠A=∠C
（1) 已知:如图6-3，在平行四边形ABCD中， E，F 是对角线AC上的两点，且AE=CF． 求证：BE = DF．
证明:∵四边形ABCD是平行四边形 ∴AB = CD AB // CD ∴∠BAE=∠DCF 又∵AE=CF ∴△BAE≌△DCF ∴BE=DF
（2）已知平行四边形一个内角的度数，能确 定其他三个内角的度数吗？说说你的理由。
经历了实践与探索,你有什么感受和收获? 能给自己一个客观的评价吗?这节课你学 到了什么？
2.这节课与同伴合作交流中，你向同伴学到 了什么？
3.本节课在知识和方法对你有什么启发?
考一考1. ABCD中， ∠B=600，则∠A=——， ∠C=——， ∠D=——.2. ABCD中∠A比∠B大200，则∠C=——. ABCD中，AB=3cm，BC=5cm， 则AD=——，CD=——.4.如果 ABCD的周长为40cm，ᅀABC的周长为25cm，则对角线AC的长是（ ）.A 5cm B 15cm C 6cm D 16cm