初中数学第六章 平行四边形2 平行四边形的判定教课内容课件ppt

这是一份初中数学第六章 平行四边形2 平行四边形的判定教课内容课件ppt，共17页。PPT课件主要包含了开动脑筋，平行四边形判定，看谁最快，请你帮忙，平行四边形的判定，平行四边形的判别方法，开心一练等内容，欢迎下载使用。
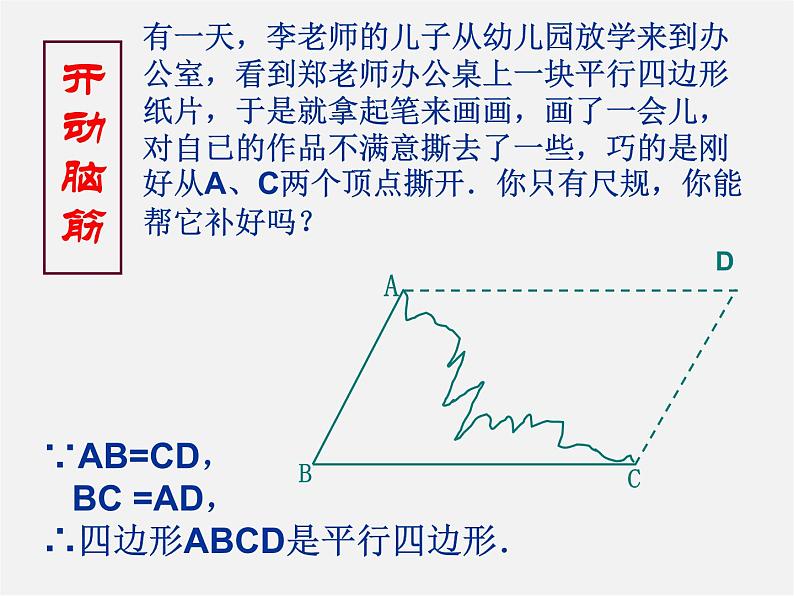
有一天，李老师的儿子从幼儿园放学来到办公室，看到郑老师办公桌上一块平行四边形纸片，于是就拿起笔来画画，画了一会儿，对自已的作品不满意撕去了一些，巧的是刚好从A、C两个顶点撕开．你只有尺规，你能帮它补好吗？
∵AB=CD， BC =AD，∴四边形ABCD是平行四边形．
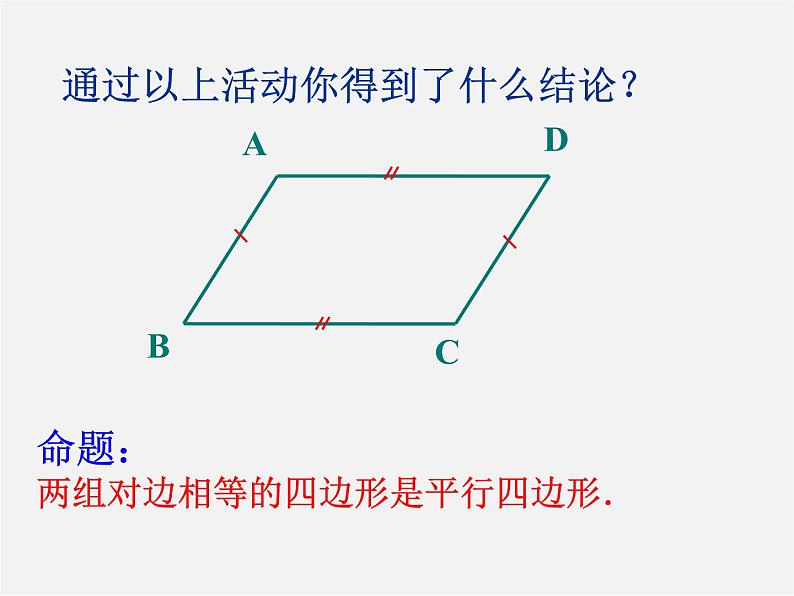
通过以上活动你得到了什么结论？
命题：两组对边相等的四边形是平行四边形．
已知：四边形ABCD， AB=CD，AD=BC ．求证：四边形ABCD是平行四边形．
连结AC，∵ AB=CD，AD=BC （已知） 又∵ AC=AC （公共边）∴△ABC≌△CDA（SSS）
∴∠1=∠2，∠3=∠4（全等三角形的对应边相等）∴ AB∥CD，AD∥BC （内错角相等，两直线平行）∴四边形ABCD是平行四边形．
平行四边形的判定定理1： 两组对边分别相等的四边形是平行四边形．
∵AB＝CD，AD＝BC（已知） ∴四边形ABCD是平行四边形． （两组对边分别相等的四边形是平行四边形．）
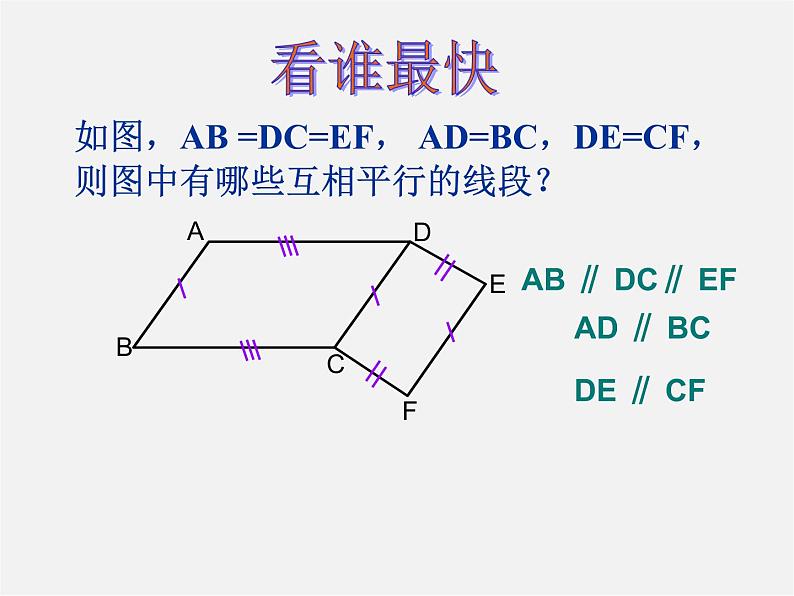
如图，AB =DC=EF， AD=BC，DE=CF，则图中有哪些互相平行的线段？
AB ∥ DC∥ EF
学习了平行四边形后，小明回家用细木棒钉制了一个平行四边形．第二天，小明拿着自己动手做的平行四边形向同学们展示． 小辉却问：你凭什么确定这四边形就是平行四边形呢？ 大家都困惑了……
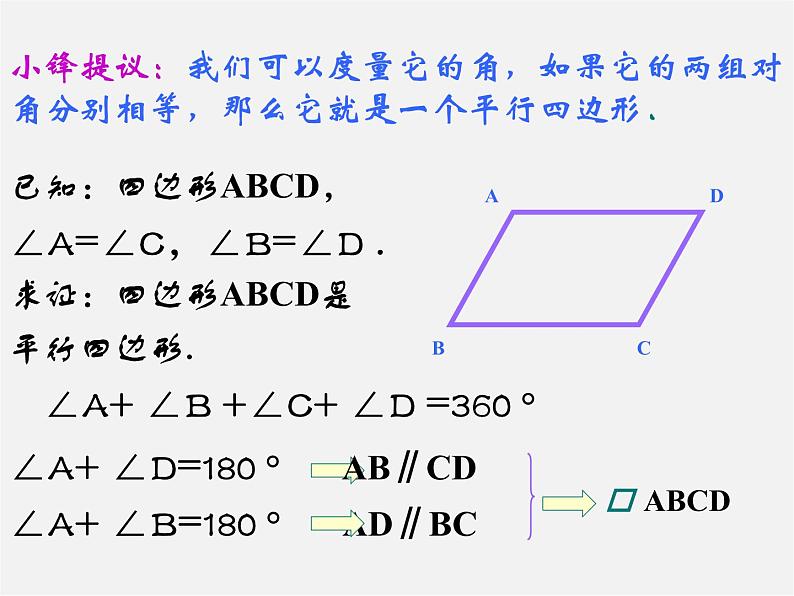
∠A+ ∠B=180 ° AD∥BC
小锋提议：我们可以度量它的角，如果它的两组对角分别相等，那么它就是一个平行四边形．
已知：四边形ABCD， ∠A=∠C，∠B=∠D ．求证：四边形ABCD是平行四边形．
∠A+ ∠D=180 ° AB∥CD
∠A+ ∠B +∠C+ ∠D =360 °
已知：四边形ABCD，∠A=∠C，∠B=∠D．求证：四边形ABCD是平行四边形．
∵∠A=∠C，∠B=∠D（已知）又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °
即∠A+ ∠B=180 °∴ AD∥BC （同旁内角互补，两直线平行）
同理可证AB∥CD ．∴四边形ABCD是平行四边形．
平行四边形的判定定理2： 两组对角分别相等的四边形是平行四边形．
∵ ∠A=∠C，∠B=∠D （已知） ∴四边形ABCD是平行四边形（两组对角分别相等的四边形是平行四边形． ）
小丽却说：“我可以不用任何作图工具，只要两条细绳就能判断它是不是平行四边形．” 只见小丽用两条细绳做四边形的对角线，并在两条对角线的交点处作了个记号．然后分别把两条对角线沿记号点对折，发现它们被记号点分成的两段线段都能重合，小丽高兴地说：“这的确是个平行四边形！”
你认为小丽的做法有根据吗？
已知：四边形ABCD中， AC，BD交于点O， 且OA=OC，OB=OD ．求证：四边形ABCD是平行四边形．
证明：∵ AO = CO ，BO = DO ，∠1=∠2
∴四边形ABCD是平行四边形．（两组对边分别平行的四边形是平行四边形．）
已知：如图，四边形对角线相交于点， 且OA=OC，OB=OD．求证：四边形ABCD是平行四边形．
证明：在△AOB和△COD中
∴ △AOB ≌ △COD (SAS)
∴四 边形ABCD是平行四边形．（两组对边分别相等的四 边形是平行四边形 ．）
平行四边形的判定定理3： 对角线互相平分的四边形是平行四边形．
∵ OA=OC，OB=OD（已知） ∴四边形ABCD是平行四边形（对角线互相平分的四边形是平行四边形 ．）
（1）根据定义：两组对边分别平行的四边形叫做平行四边形．（2）两组对边分别相等的四边形是平行四边形． (3)两组对角分别相等的四边形是平行四边形．（4）两条对角线互相平分的四边形是平行四边形．
根据下列条件，不能判定一个四边形为平行四边形的是（ ）（A）两组对边分别相等．（B）两条对角线互相平分．（C）两条对角线相等．（D）两组对边分别平行．