北师大版九年级上册1 用树状图或表格求概率背景图课件ppt

这是一份北师大版九年级上册1 用树状图或表格求概率背景图课件ppt，共14页。PPT课件主要包含了学习目标，导学一，检测一，检测二，自主提升等内容，欢迎下载使用。
1、运用树状图或列表的方法计算事件发生的概率；2、利用概率解决一些简单的实际问题。
例1 小明、小颖和小凡做“石头、剪刀、布”游戏．游戏规则如下：由小明和小颖做“石头、剪刀、布”的游戏，如果两人的手势相同，那么小凡获胜；如果两人手势不同，那么按照“石头胜剪刀，剪刀胜布，布胜石头”的规则决定小明和小颖中的获胜者.假设小明和小颖每次出这三种手势的可能性相同，你认为这个游戏对三人公平吗？
解：因为小明和小颖每次出这三种手势的可能性相同，所以可以利用树状图列出所有可能出现的结果：
总共有 9 种可能的结果，每种结果出现的可能性相同．其中，两人手势相同的结果有3种：（石头，石头）（剪刀，剪刀）（布，布），所以小凡获胜的概率为小明胜小颖的结果有3种：（石头，剪刀）（剪刀，布）（布，石头），所以小明获胜的概率为小颖胜小明的结果也有3种：（剪刀，石头）（布，剪刀）（石头，布），所以小颖获胜的概率为
因此， 这个游戏对三人是公平的.
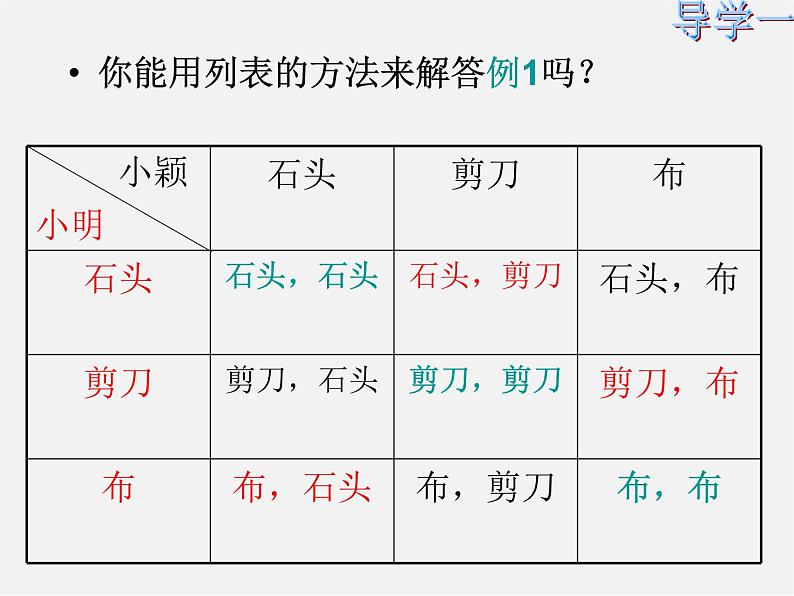
你能用列表的方法来解答例1吗？
有三张大小一样而画面不同的画片，先将每一张从中间剪开，分成上下两部分；然后把三张画片的上半部分都放在第一个盒子中，把下半部分都放在第二个盒子中．分别摇匀后，从每个盒子中各随机地摸出一张，求这两张恰好能拼成原来的一幅画的概率.
小明和小军两人一起做游戏．游戏规则如下：每人从1，2，…，12中任意选择一个数，然后两人各掷一次质地均匀的骰子，谁事先选择的数等于两人掷得的点数之和谁就获胜；如果两人选择的数都不等于掷得的点数之和，就再做一次上述游戏，直至决出胜负.如果你是游戏者，你会选择哪个数？
在本节课的“石头、剪刀、布”游戏中，小凡没有参与活动，有“任人宰割”的感觉，于是他们修改游戏规则如下：三人同时做“石头、剪刀、布”游戏，如果三人的手势都相同或三人的手势互不相同，那么三人不分胜负；如果有两个人的手势相同，那么按照“石头胜剪刀，剪刀胜布，布胜石头”的规则决定胜负（有可能有两个胜者）．这个游戏对三人公平吗？先算一算，再做一做.
1．准备两组相同的牌，每组三张且大小一样，三张牌的牌面数字分别是 1，2，3 ．从每组牌中各摸出一张牌.（1）两张牌的牌面数字和等于 1 的概率是多少？（2）两张牌的牌面数字和等于 2 的概率是多少？（3）两张牌的牌面数字和为几的概率最大？（4）两张牌的牌面数字和大于 3 的概率是多少？
2．经过某路口的行人，可能直行，也可能左拐或右拐．假设这三种可能性相同，现有两人经过该路口，求下列事件的概率：（1）两人都左拐； （2）恰好有一人直行，另一人左拐；（3）至少有一人直行．
3．掷两枚质地均匀的骰子，求下列事件的概率：（1）至少有一枚骰子的点数为 1； （2）两枚骰子的点数和为奇数；（3）两枚骰子的点数和大于 9；（4）第二枚骰子的点数整除第一枚骰子的点数.
4．小明和小军做掷骰子游戏，两人各掷一枚质地均匀的骰子.（1）若两人掷得的点数之和为奇数，则小军获胜，否则小明获胜．这个游戏对双方公平吗？为什么？（2）若两人掷得的点数之积为奇数，则小军获胜，否则小明获胜．这个游戏对双方公平吗？为什么？