高中数学人教B版 (2019)必修 第一册第二章 等式与不等式2.2 不等式2.2.1 不等式及其性质第1课时导学案

这是一份高中数学人教B版 (2019)必修 第一册第二章 等式与不等式2.2 不等式2.2.1 不等式及其性质第1课时导学案，共11页。学案主要包含了作差法比较大小，利用不等式的性质判断或证明等内容，欢迎下载使用。
第1课时 不等式及其性质
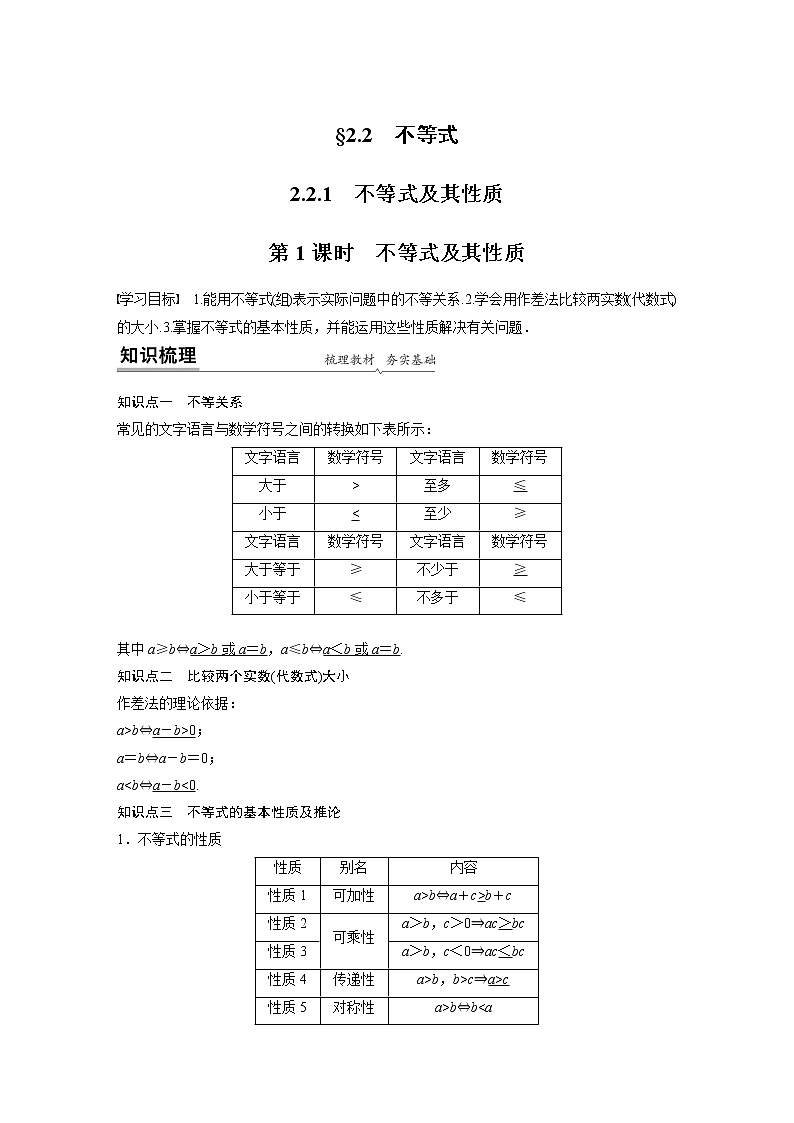
学习目标 1.能用不等式(组)表示实际问题中的不等关系.2.学会用作差法比较两实数(代数式)的大小.3.掌握不等式的基本性质，并能运用这些性质解决有关问题．
知识点一 不等关系
常见的文字语言与数学符号之间的转换如下表所示：
其中a≥b⇔a＞b或a＝b，a≤b⇔a＜b或a＝b.
知识点二 比较两个实数(代数式)大小
作差法的理论依据：
a>b⇔a－b>0；
a＝b⇔a－b＝0；
ad的充要条件是a＋c>b＋d.( × )
一、作差法比较大小
例1 已知a，b均为正实数．试利用作差法比较a3＋b3与a2b＋ab2的大小．
解 ∵a3＋b3－(a2b＋ab2)＝(a3－a2b)＋(b3－ab2)
＝a2(a－b)＋b2(b－a)
＝(a－b)(a2－b2)＝(a－b)2(a＋b)．
∴当a＝b时，a－b＝0，a3＋b3＝a2b＋ab2；
当a≠b时，(a－b)2>0，a＋b>0，a3＋b3>a2b＋ab2.
综上所述，a3＋b3≥a2b＋ab2.
延伸探究
1．若a>0，b>0，a5＋b5与a3b2＋a2b3的大小关系又如何？
解 (a5＋b5)－(a3b2＋a2b3)＝a5－a3b2＋b5－a2b3
＝a3(a2－b2)＋b3(b2－a2)
＝(a2－b2)(a3－b3)
＝(a－b)2(a＋b)(a2＋ab＋b2)．
∵a>0，b>0，
∴(a－b)2≥0，a＋b>0，a2＋ab＋b2>0.
∴a5＋b5≥a3b2＋a2b3.
2．对于an＋bn，你能有一个更具一般性的猜想吗？
解 若a>0，b>0，n>r，n，r∈N＋，则an＋bn≥arbn－r＋an－rbr.
反思感悟 作差法比较大小的四个步骤
跟踪训练1 若x∈R，则eq \f(x,1＋x2)与eq \f(1,2)的大小关系为________________．
答案 eq \f(x,1＋x2)≤eq \f(1,2)
解析 ∵eq \f(x,1＋x2)－eq \f(1,2)＝eq \f(2x－1－x2,21＋x2)＝eq \f(－x－12,21＋x2)≤0.
∴eq \f(x,1＋x2)≤eq \f(1,2).
二、利用不等式的性质判断或证明
例2 (1)已知b3bd
C．2a＋c>b＋3d D．2a＋3d>b＋c
答案 C
解析 由于b0，求证：eq \f(a,c－a)>eq \f(b,c－b).
证明 a>b>0⇒－a0，
所以00.
又因为a>b>0，
所以eq \f(a,c－a)>eq \f(b,c－b).
反思感悟 利用不等式的性质解决问题的注意点
(1)在解决选择题时，可利用特殊值法进行排除，注意取值时一是满足题设条件，二是取值简单，便于计算．
(2)应用不等式的性质证明时，应注意紧扣不等式的性质成立的条件，不可省略条件或跳步推导．
跟踪训练2 (多选)下列命题正确的是( )
A.eq \f(c,a)0⇒a>b
B．a>b且c>d⇒ac>bd
C．a>b>0且c>d>0⇒eq \r(\f(a,d)) >eq \r(\f(b,c))
D.eq \f(a,c2)>eq \f(b,c2)⇒a>b
答案 CD
解析 A中，eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(c,a)0))⇒eq \f(1,a)b，错误；
B中，当a＝3，b＝1，c＝－2，d＝－3时，命题显然不成立，错误；
C中，eq \b\lc\{\rc\ (\a\vs4\al\c1(a>b>0，,c>d>0))⇒eq \f(a,d)>eq \f(b,c)>0⇒eq \r(\f(a,d))>eq \r(\f(b,c))成立，正确；
D中，显然c2>0，
∴两边同乘以c2得a>b，正确．
利用不等式的性质求取值范围
典例 已知－1