人教B版 (2019)必修 第一册2.2.3 一元二次不等式的解法学案

这是一份人教B版 (2019)必修 第一册2.2.3 一元二次不等式的解法学案，共13页。

知识点一 一元二次不等式的概念
一般地，形如ax2＋bx＋c＞0的不等式称为一元二次不等式，其中a，b，c是常数，而且a≠0.一元二次不等式中的不等号也可以是“＜”“≥”“≤”等．
思考 不等式ax2＋x－1>0一定表示一元二次不等式吗？
答案 不一定．当a＝0时，表示一元一次不等式．
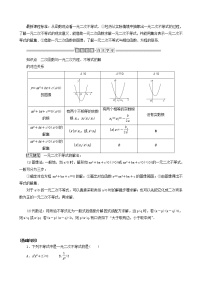
知识点二 一元二次不等式的解法
1．因式分解法
如果x1＜x2，则不等式(x－x1)(x－x2)＜0的解集是(x1，x2)，不等式(x－x1)(x－x2)＞0的解集是(－∞，x1)∪(x2，＋∞)．
2．配方法
一元二次不等式ax2＋bx＋c＞0(a≠0)通过配方总是可以变为(x－h)2＞k或(x－h)2＜k的形式，然后根据k的正负等知识，就可以得到原不等式的解集．
1．不等式3x2－2x＋1＞0的解集为( )
A.eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(－1＜x＜\f(1,3))))) B.eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(\f(1,3)＜x＜1))))
C．∅ D．R
答案 D
解析 因为Δ＝(－2)2－4×3×1＝4－12＝－8＜0，
所以不等式3x2－2x＋1＞0的解集为R.
2．不等式(3x－2)(2－x)≥0的解集是( )
A.eq \b\lc\[\rc\](\a\vs4\al\c1(\f(2,3)，2)) B.eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，\f(2,3)))∪[2，＋∞)
C.eq \b\lc\[\rc\](\a\vs4\al\c1(\f(3,2)，2)) D.eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(2,3)，2))
答案 A
解析 原不等式等价于eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(2,3)))(x－2)≤0，
解得eq \f(2,3)≤x≤2.
3．不等式x(x－2)>0的解集为________，不等式x(x－2)