高中数学5.3.2 事件之间的关系与运算导学案及答案

这是一份高中数学5.3.2 事件之间的关系与运算导学案及答案，共11页。学案主要包含了事件的关系，事件的运算，利用互斥等内容，欢迎下载使用。
5．3.2　事件之间的关系与运算
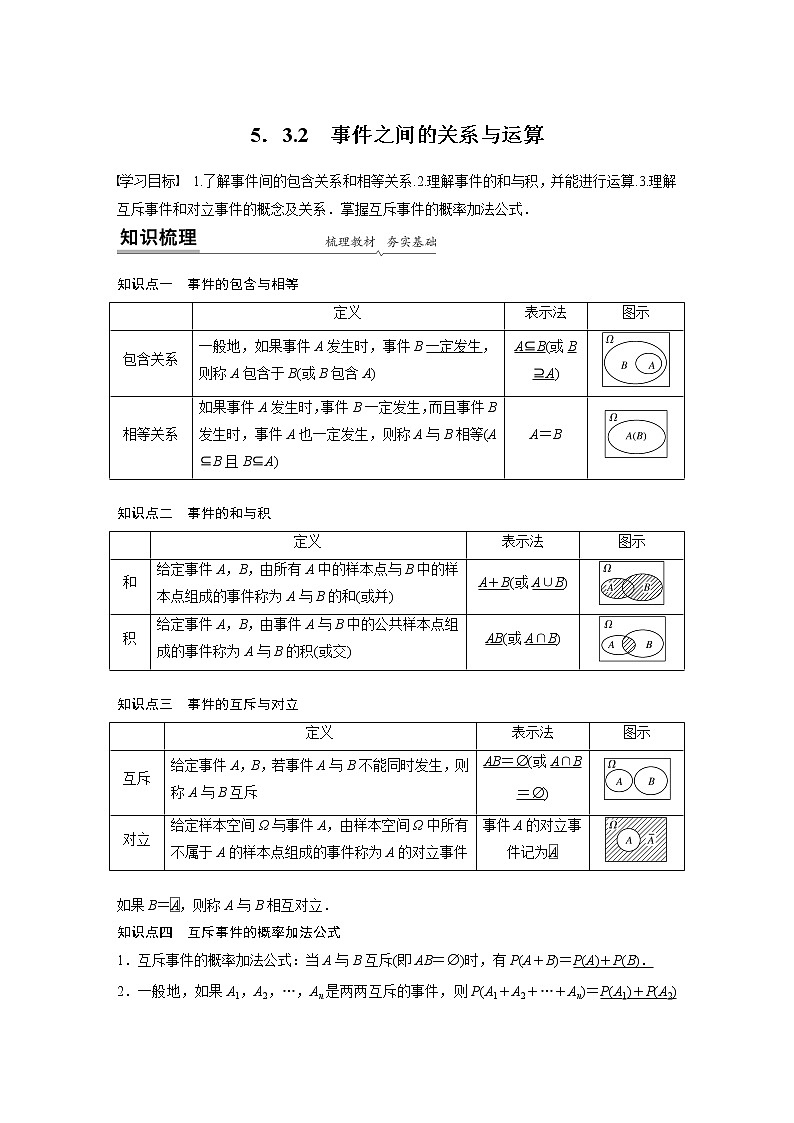
学习目标　1.了解事件间的包含关系和相等关系.2.理解事件的和与积，并能进行运算.3.理解互斥事件和对立事件的概念及关系．掌握互斥事件的概率加法公式．

知识点一　事件的包含与相等

定义
表示法
图示
包含关系
一般地，如果事件A发生时，事件B一定发生，则称A包含于B(或B包含A)
A⊆B(或B⊇A)

相等关系
如果事件A发生时，事件B一定发生，而且事件B发生时，事件A也一定发生，则称A与B相等(A⊆B且B⊆A)
A＝B


知识点二　事件的和与积

定义
表示法
图示
和
给定事件A，B，由所有A中的样本点与B中的样本点组成的事件称为A与B的和(或并)
A＋B(或A∪B)

积
给定事件A，B，由事件A与B中的公共样本点组成的事件称为A与B的积(或交)
AB(或A∩B)


知识点三　事件的互斥与对立

定义
表示法
图示
互斥
给定事件A，B，若事件A与B不能同时发生，则称A与B互斥
AB＝∅(或A∩B＝∅)

对立
给定样本空间Ω与事件A，由样本空间Ω中所有不属于A的样本点组成的事件称为A的对立事件
事件A的对立事件记为


如果B＝，则称A与B相互对立．
知识点四　互斥事件的概率加法公式
1．互斥事件的概率加法公式：当A与B互斥(即AB＝∅)时，有P(A＋B)＝P(A)＋P(B)．
2．一般地，如果A1，A2，…，An是两两互斥的事件，则P(A1＋A2＋…＋An)＝P(A1)＋P(A2)＋…＋P(An)．
3．P(A)＋P()＝1.
1．互斥事件一定对立．(　×　)
2．对立事件一定互斥．(　√　)
3．事件A与B的和事件的概率一定大于事件A的概率．(　×　)
4．事件A与B互斥，则有P(A)＝1－P(B)．(　×　)

一、事件的关系
例1　某小组有3名男生和2名女生，从中任选2名同学参加演讲比赛，判断下列每对事件是不是互斥事件，如果是，再判断它们是不是对立事件：
(1)“恰有1名男生”与“恰有2名男生”；
(2)“至少有1名男生”与“全是男生”；
(3)“至少有1名男生”与“全是女生”；
(4)“至少有1名男生”与“至少有1名女生”．
解　从3名男生和2名女生中任选2人有如下三种结果：2名男生，2名女生，1男1女．
(1)“恰有1名男生”指1男1女，与“恰有2名男生”不能同时发生，它们是互斥事件；但是当选取的结果是2名女生时，两事件都不发生，所以它们不是对立事件．
(2)“至少1名男生”包括2名男生和1男1女两种结果，与事件“全是男生”可能同时发生，所以它们不是互斥事件．
(3)“至少1名男生”与“全是女生”不可能同时发生，所以它们互斥，由于它们必有一个发生，所以它们是对立事件．
(4)“至少有1名女生”包括1男1女与2名女生两种结果，当选出的是1男1女时，“至少有一名男生”与“至少有一名女生”同时发生，所以它们不是互斥事件．
反思感悟　判断事件间关系的方法
(1)要考虑试验的前提条件，无论是包含、相等，还是互斥、对立其发生的条件都是一样的．
(2)考虑事件间的结果是否有交事件，可考虑利用维恩图分析，对较难判断关系的，也可列出全部结果，再进行分析．
跟踪训练1　(1)从装有5个红球和3个白球的口袋内任取3个球，那么下列各对事件中，互斥而不对立的是(　　)
A．至少有一个红球与都是红球
B．至少有一个红球与都是白球
C．至少有一个红球与至少有一个白球
D．恰有一个红球与恰有两个红球
(2)一个人打靶时连续射击两次，事件“至少有一次中靶”的互斥事件是(　　)
A．至多有一次中靶 B．只有一次中靶
C．两次都中靶 D．两次都不中靶
答案　(1)D　(2)D
解析　(1)根据互斥事件与对立事件的定义判断．A中两事件不是互斥事件，事件“三个球都是红球”是两事件的交事件；B中两事件是对立事件；C中两事件能同时发生，如“恰有一个红球和两个白球”，故不是互斥事件；D中两事件是互斥而不对立事件．
(2)A，B，C中的事件均能与事件“至少有一次中靶”同时发生，故A，B，C错误，选D.
二、事件的运算
例2　在掷骰子的试验中，可以定义许多事件．例如，事件C1＝{出现1点}，事件C2＝{出现2点}，事件C3＝{出现3点}，事件C4＝{出现4点}，事件C5＝{出现5点}，事件C6＝{出现6点}，事件D1＝{出现的点数不大于1}，事件D2＝{出现的点数大于3}，事件D3＝{出现的点数小于5}，事件E＝{出现的点数小于7}，事件F＝{出现的点数为偶数}，事件G＝{出现的点数为奇数}，请根据上述定义的事件，回答下列问题：
(1)请举出符合包含关系、相等关系的事件；
(2)利用和事件的定义，判断上述哪些事件是和事件．
解　(1)因为事件C1，C2，C3，C4发生，则事件D3必发生，所以C1⊆D3，C2⊆D3，C3⊆D3，C4⊆D3.
同理可得，事件E包含事件C1，C2，C3，C4，C5，C6；事件D2包含事件C4，C5，C6；事件F包含事件C2，C4，C6；事件G包含事件C1，C3，C5.
且易知事件C1与事件D1相等，即C1＝D1.
(2)因为事件D2＝{出现的点数大于3}＝{出现4点或出现5点或出现6点}，
所以D2＝C4∪C5∪C6(或D2＝C4＋C5＋C6)．
同理可得，D3＝C1＋C2＋C3＋C4，E＝C1＋C2＋C3＋C4＋C5＋C6，F＝C2＋C4＋C6，G＝C1＋C3＋C5.
反思感悟　事件间的运算方法
(1)利用事件间运算的定义．列出同一条件下的试验所有可能出现的结果，分析并利用这些结果进行事件间的运算．
(2)利用维恩图．借助集合间运算的思想，分析同一条件下的试验所有可能出现的结果，把这些结果在图中列出，进行运算．
跟踪训练2　盒子里有6个红球，4个白球，现从中任取3个球，设事件A＝{3个球中有一个红球，两个白球}，事件B＝{3个球中有两个红球，一个白球}，事件C＝{3个球中至少有一个红球}，事件D＝{3个球中既有红球又有白球}．则：
(1)事件D与事件A，B是什么样的运算关系？
(2)事件C与事件A的交事件是什么事件？
解　(1)对于事件D，可能的结果为1个红球2个白球或2个红球1个白球，故D＝A＋B.
(2)对于事件C，可能的结果为1个红球2个白球，2个红球1个白球或3个红球，故C∩A＝A.
三、利用互斥、对立事件求概率
例3　某射击运动员在一次射击中射中10环、9环、8环、7环、7环以下的概率分别为0.1,0.2,0.3,0.3,0.1.计算这个运动员在一次射击中：
(1)射中10环或9环的概率；
(2)至少射中7环的概率．
解　设“射中10环”、“射中9环”、“射中8环”、“射中7环”、“射中7环以下”的事件分别为A，B，C，D，E，它们两两互斥，则
(1)P(A＋B)＝P(A)＋P(B)＝0.1＋0.2＝0.3.
所以射中10环或9环的概率为0.3.
(2)因为射中7环以下的概率为0.1，所以由对立事件的概率公式得，至少射中7环的概率为1－0.1＝0.9.
延伸探究
在本例条件下，求射中环数小于8环的概率．
解　事件“射中环数小于8环”包含事件D“射中7环”与事件E“射中7环以下”两个事件，则P(射中环数小于8环)＝P(D＋E)＝P(D)＋P(E)＝0.3＋0.1＝0.4.
反思感悟　互斥事件、对立事件概率的求解方法
(1)互斥事件的概率的加法公式P(A＋B)＝P(A)＋P(B)．
(2)当求解的问题中有“至多”“至少”“最少”等关键词语时，常常考虑其反面，通过求其反面，然后转化为所求问题．
跟踪训练3　某公务员去开会，他乘火车、轮船、汽车、飞机去的概率分别是0.3,0.2,0.1,0.4.
求：(1)他乘火车或飞机去的概率；
(2)他不乘轮船去的概率．
解　设乘火车去开会为事件A，乘轮船去开会为事件B，乘汽车去开会为事件C，乘飞机去开会为事件D，它们彼此互斥．
(1)P(A＋D)＝P(A)＋P(D)＝0.3＋0.4＝0.7.
(2)P＝1－P(B)＝1－0.2＝0.8.



用方程的思想求概率
典例　袋中有外形、质量完全相同的红球、黑球、黄球、绿球共12个，从中任取一球，得到红球的概率是，得到黑球或黄球的概率是，得到黄球或绿球的概率也是.
(1)试分别求得到黑球、黄球、绿球的概率；
(2)从中任取一球，求得到的不是红球或绿球的概率．
解　(1)从袋中任取一球，记事件“得到红球”“得到黑球”“得到黄球”“得到绿球”分别为A，B，C，D，它们两两互斥，
则P(A)＝，P(B＋C)＝P(B)＋P(C)＝，P(C＋D)＝P(C)＋P(D)＝，P(B＋C＋D)＝P(B)＋P(C)＋P(D)＝1－P(A)＝1－＝.
联立
解得P(B)＝，P(C)＝，P(D)＝，
故得到黑球，得到黄球，得到绿球的概率分别为，，.
(2)事件“得到红球或绿球”可表示为事件A＋D，由(1)及互斥事件的概率加法公式得P(A＋D)＝P(A)＋P(D)＝＋＝，
故得到的不是红球或绿球的概率P＝1－P(A＋D)＝1－＝.
[素养提升]　(1)求概率可以考虑用对立事件、互斥事件的概率加法公式求解．如果有多个待求量，可以列方程组求解．
(2)理解运算策略，选择运算方法，求得运算结果，这都是数学核心素养之数学运算的具体体现．

1．同时掷两枚硬币，向上面都是正面为事件A，向上面至少有一枚是正面为事件B，则有(　　)
A．A⊆B B．A⊇B C．A＝B D．A