初中数学北师大版九年级下册2 圆的对称性图文ppt课件

这是一份初中数学北师大版九年级下册2 圆的对称性图文ppt课件，共60页。PPT课件主要包含了错在哪里，破镜重圆，课堂小结，你会做吗等内容，欢迎下载使用。
圆是一种美丽的图形，春秋战国时期，墨翟在其所著《墨经》一书中就曾明确指出：“圜，一中同长也。”毕达哥拉斯曾经说过：“一切立体图形中，最美的是球形；一切平面图形中最美的是圆形。”
那么，圆到底美在哪里？
九年级数学(下)第三章圆
3.2 圆的对称性(1) -----垂径定理

3.2 圆的对称性
1、什么是轴对称图形？我们在直线形中学过哪些轴对称图形？
如果一个图形沿一条直线对折，直线两旁的部分能够互相重合，那么这个图形叫轴对称图形。如线段、角、等腰三角形、矩形、菱形、等腰梯形、正方形
如果是,它的对称轴是什么? 你能找到多少条对称轴？
你是用什么方法解决上述问题的?
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
可利用折叠的方法即可解决上述问题.
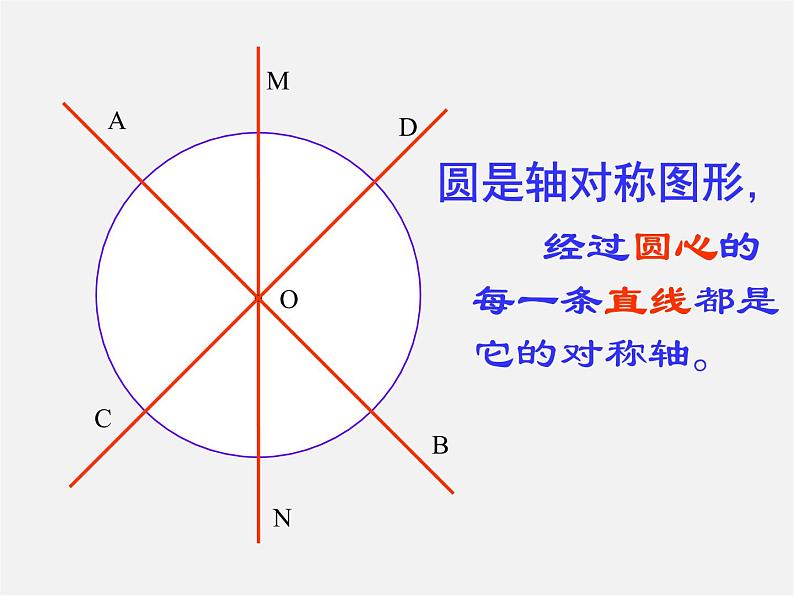
经过圆心的每一条直线都是它的对称轴。
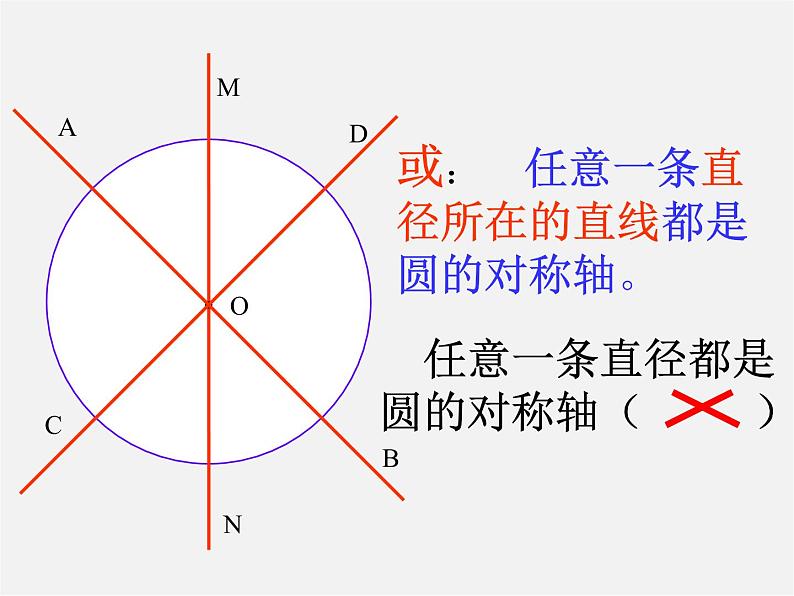
或： 任意一条直径所在的直线都是圆的对称轴。
任意一条直径都是圆的对称轴（ ）
圆上任意两点间的部分叫做圆弧,简称弧.
直径将圆分成两部分,每一部分都 叫做半圆(如弧ABC).
连接圆上任意两点间的线段叫做弦(如弦AB).
经过圆心的弦叫做直径(如直径AC).
同心圆:圆心相同、半径不相等的两个圆叫做同心圆。
弓形:由弦及其所对的弧组成的图形叫做弓形.
等圆、等弧:能够重合的两个圆叫做等圆. 在同圆或等圆中,能够互相重合的弧叫做等弧.
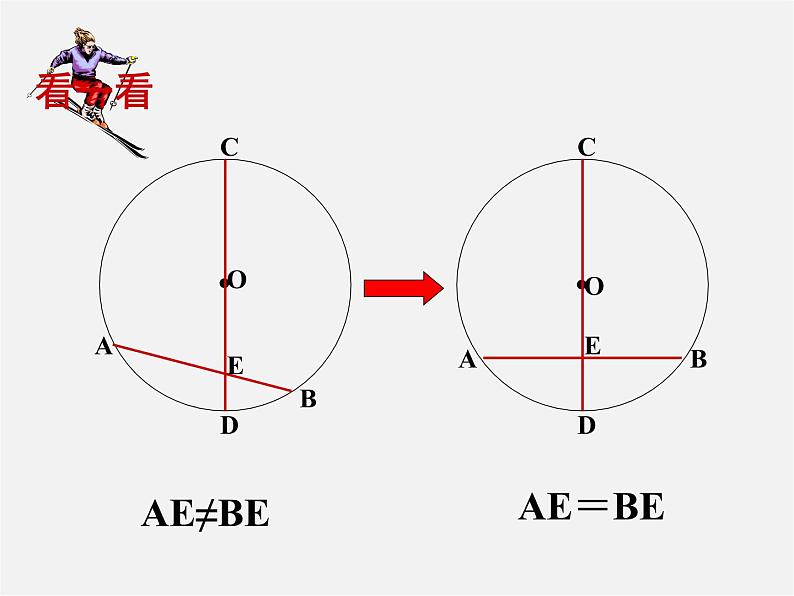
你能发现图中有哪些等量关系?与同伴说说你的想法和理由.
作直径CD,使CD⊥AB,垂足为M.
下图是轴对称图形吗?如果是,其对称轴是什么?
在Rt△OAM和Rt△OBM中,
∵OA=OB，OM=OM，
∴Rt△OAM≌Rt△OBM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
垂直于弦的直径平分这条弦，并且平分弦所对的两条弧.
（1）直径（2）垂直于弦
（3）平分弦（4）平分弦所对的优弧（5）平分弦所对的劣弧
定理: 垂直于弦的直径平分弦, 并且平分弦所对的两条弧.
杨老师提示:垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
在下列图形中，找出能利用垂径定理的图形
例1、如图，已知在⊙O中，弦AB的长为8厘米，圆心O到AB的距离为3厘米，求⊙O的半径。
解：连结OA. 过O作OE⊥AB，垂足为E，则OE＝3厘米，AE＝BE。∵AB＝8厘米 ∴AE＝4厘米 在Rt △AOE中，根据勾股定理有OA＝5厘米 ∴⊙O的半径为5厘米
方法总结：利用垂径定理解题，需要利用三角形AOE,如果有，直接用；如果没有，就需要作出相应三角形。请大家要牢记这一点！
3.2 圆的对称性(2) ----垂径定理的推论
平分弦（不是直径）的直径垂直于弦,并且平 分弦所对的两条弧.
垂径定理的逆定理（推论）
AB是⊙O的一条弦,且AM=BM.
左图是轴对称图形吗?如果是,其对称轴是什么?
一个圆的任意两条直径总是互相平分，但是它们不一定互相垂直。因此这里的弦如果是直径，结论就不一定成立。
垂径定理逆定理： 平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。
你可以写出相应的命题吗?相信自己是最棒的!
如图,在下列五个条件中:
只要具备其中两个条件,就可推出其余三个结论.
垂直于弦的直径平分弦,并且平分弦所的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.
平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.
平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.
（1）：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧
已知：CD是直径，AB是弦，并且CD平分AB
（2）：弦的垂直平分线经过圆心，并且平分弦所对的两条弧
（3）：平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧
以上都是垂径定理的推论（1）
（1）垂直于弦的直线平分弦，并且平分弦所对的弧…………………………………………..( )
（2）弦所对的两弧中点的连线，垂直于弦，并且经过圆心……………………………………..( )
（3）圆的不与直径垂直的弦必不被这条直径平分…………………………………………...( )
（4）平分弦的直径垂直于弦，并且平分弦所对的两条弧………………………………………( )
（5）圆内两条非直径的弦不能互相平分（ ）
按图填空：在⊙O中，（1）若MN⊥AB，MN为直径，则________，________，________；（2）若AC＝BC，MN为直径，AB不是直径，则则_______，_______，______；（3）若MN⊥AB，AC＝BC，则________，________，________；（4）若 AC＝BC ，MN为直径，则________，________，________．
挑战自我垂径定理的推论（2）
如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?
老师提示: 这两条弦在圆中位置有两种情况:
垂径定理的推论 圆的两条平行弦所夹的弧相等.
如果圆的两条弦互相平行，那么这两条弦所夹的弧相等.
例2 已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点。求证：AC＝BD。
证明：过O作OE⊥AB，垂足为E，则AE＝BE，CE＝DE。AE－CE＝BE－DE。所以，AC＝BD
解决有关弦的问题，经常是过圆心作弦的垂线，或作垂直于弦的直径，连结半径等辅助线，为应用垂径定理创造条件。
在a,d,r,h中，已知其中任意两个量,可以求出其它两个量.
⒉作AB的垂直平分线 CD，交弧AB于点E.
点E就是所求弧AB的中点。
变式一： 求弧AB的四等分点。
变式二：你能确定 弧AB的圆心吗？
等分弧时一定要作弧所夹弦的垂直平分线。
●作AB的垂直平分线CD。
●作AT．BT的垂直 平分线EF．GH
作弦AB．AC及它们的垂直平分线m．n，交于O点；以O为圆心，OA为半径作圆。
弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
3.2 圆的对称性(3) -----垂径定理的应用
①直线MN过圆心②MN⊥AB
④ ⑤
①直线MN过圆心③ AC=BC
推论1. (1)平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。
② MN⊥AB ③ AC=BC
推论1:(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
推论1: (3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧
圆的两条平行弦所夹的弧相等。
垂径定理的应用(测公路的弯道的半径 )
解：连接OC. 设弯路的半径为Rm，则0F=（R-90）m. ∵OE⊥CD， ∴CF=1/2CD=1/2×600=300（m）. 根据勾股定理，得OC2=CF2+OF2， 即 R2=3002+（R-90）2 解这个方程，得R=545. 所以，这段弯路的半径为545m.
例2、1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).
你是第一个告诉同学们解题方法和结果的吗？
解：如图，用 表示桥拱， 所在圆的圆心为O，半径为Rm，经过圆心O作弦AB的垂线OD，D为垂足，与 相交于点C.根据垂径定理，D是AB的中点，C是 的中点，CD就是拱高.由题设
在Rt△OAD中，由勾股定理，得
解得 R≈27.9（m）.
答：赵州石拱桥的桥拱半径约为27.9m.
变式1：如图，在⊙O中，CD是直径，AB是弦，且CD⊥AB，已知CD = 20，CM = 4，求AB。
变式2、如图为一圆弧形拱桥，半径OA = 10m，拱高为4m，求拱桥跨度AB的长。
在直径为650mm的圆柱形油槽内装入一些油后，截面如图所示.若油面宽AB = 600mm，求油的最大深度.
1、要把实际问题转变成一个数学问题来解决.
2、熟练地运用垂径定理及其推论、勾股定理，并用方程的思想来解决问题.
3、对于一个圆中的弦长a、圆心到弦的距离d、圆半径r、弓形高h，这四个量中，只要已知其中任意两个量，就可以求出另外两个量，如图有：
1.已知：AB是⊙O直径，CD是弦，AE⊥CD，BF⊥CD求证：EC＝DF
2.如图,圆O与矩形ABCD交于E、F、G、H,EF=10,HG=6,AH=4.求BE的长.
1.请说出本节所学习的主要内容。2.还有什么疑惑请提出来
形成天才的决定因素应该是勤奋.
3.2 圆的对称性(4) ---弦、弧、圆心角的关系
圆是轴对称图形,圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
圆也是中心对称图形,它的对称中心就是圆心.
用旋转的方法可以得到:
一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.
这是圆特有的一个性质:圆的旋转不变性
请问圆是否是中心对称图形呢？
什么叫圆心角？顶点在圆心的角叫做圆心角。 在⊙O中有两个相等的圆心角，想一想这两个圆心角所对的两条弦是否相等？所对的两条弧是否相等？
弦AB和弦ＣＤ对应的弦心距什么关系？
在同圆或等圆中，如果两个圆心角相等，那么它们所对的弦相等，所对的弧也相等。　　　　　　　　
∵ ∠ AOB= ∠ COD
圆心角所对的弧相等， 圆心角所对的弦相等， 圆心角所对弦的弦心距相等。
推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中的一组量相等，那么它们所对应的其余各组量都分别相等。
在同圆或等圆中(前提)
1.如图，AB、CD是⊙O的两条弦，OE、OF为AB、CD的弦心距，如果AB＝CD，那么 ， ， ；如果OE＝OF，那么 ， ， ；如果弧AB＝弧CD，那么 ， ， ；如果∠AOB＝∠COD，那么 ， ， 。2.下列说法正确吗？为什么？在⊙O和⊙O’中，∵∠AOB＝∠A’O’B’∴AB＝A’B’在⊙O和⊙O’中，∵AB＝A’B’，∴弧AB＝弧A’B’
注意前提：在同圆或等圆中
1、如图，在⊙O中，弧AB＝弧AC，∠B＝70°.求∠C 度数.
2、如图，AB是直径，BC＝CD＝DE，∠BOC＝40°则∠AOE= 。
例1. 已知：如图，点P在⊙O上,点O在∠EPF的平分线上，∠ EPF的两边交⊙O于点A和B。求证：PA=PB.
例2已知：如图，点O在∠EPF的平分线上，⊙O和∠ EPF的两边分别交于点A，B和C，D。求证：AB＝CD
例3. 已知：如图， ⊙O的弦AB，CD相交于点P，∠DPO=∠ BPO 。求证：AB＝CD
例4.已知：如图， ⊙O的弦AB，CD相交于点P，过P、O的直径为MN，∠APO=∠ CPO 。求证：PB＝PD
例5.已知：如图，AD=BC.求证：AB＝CD
例6.已知：在⊙O中，弦AB所对的劣弧为圆的1/3，圆的半径为2cm。求AB的长。
例7.已知AB和CD为⊙O的两条直径，弦EC//AB,弧EC的度数为40°，求∠BOD的度数。
例8已知：如图， PB＝PD. 求证： AB=CD 。
例9.已知：如图， ⊙O的两条半径OA⊥OB，C、D是弧AB的三等分点。求证：CD＝AE＝BF。