初中数学北师大版九年级下册第三章 圆8 圆内接正多边形教课内容课件ppt

这是一份初中数学北师大版九年级下册第三章 圆8 圆内接正多边形教课内容课件ppt，共9页。PPT课件主要包含了图片欣赏，圆内接正多边形，中心角等内容，欢迎下载使用。
什么样的图形是正多边形？
各边相等,各角也相等的多边形是正多边形.
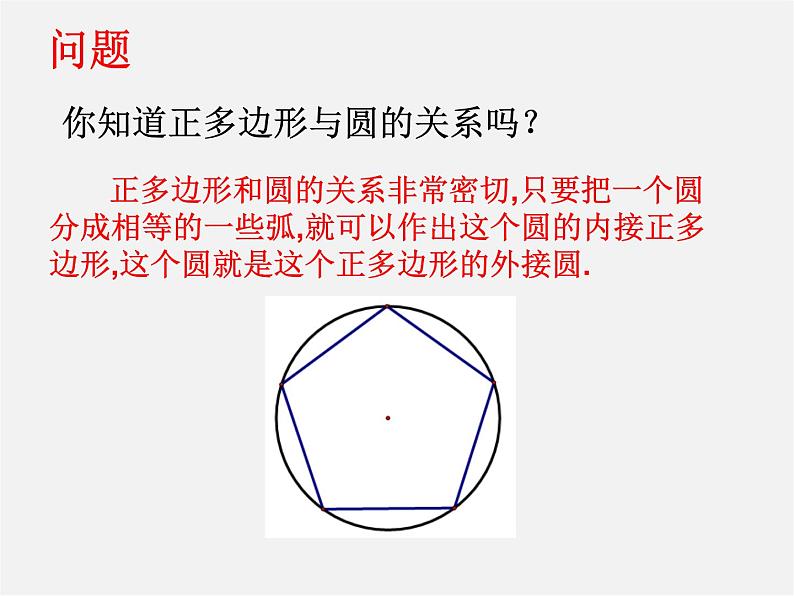
你知道正多边形与圆的关系吗？
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
顶点都在同一个圆上的正多边形叫做圆内接正多边形。这个圆叫做该正多边形的外接圆。
把一个圆n等分（n≥3），依次连接各分点，我们就可以作出一个圆内接正多边形。 如图3－35，五边形ABCDE是圆O的内接正五边形，圆心O叫做这个正五边形的中心；OA是这个正五边形的半径；∠AOB是这个正五边形的中心角；OM⊥BC，垂足为M，OM是这个正五边形的的边心距。在其他的正多边形中也有同样的定义。
正n边形的一个内角的度数是多少？中心角呢？正多边形的中心角与外角的大小有什么关系？
例：如图3－36，在圆内接正六边形ABCDEF中，半径OC=4，OG⊥BC ，垂足为点G，求正六边形的中心角、边长和边心距。
用尺规作一个已知圆的内接正六边形
作法如下：（1）以圆周上任意一点为圆心，以圆的半径为半径作弧，与圆周交于一点；（2）以得到的交点为圆心，以圆的半径为半径作弧与圆周交于另一点，依次下去，在圆周上等到六个点；（3）依次连接这六个点，就得到了这个圆的内接正六边形。
你还能借助尺规作出圆内接正四边形吗？