人教版七年级下册5.3.1 平行线的性质教学演示课件ppt

这是一份人教版七年级下册5.3.1 平行线的性质教学演示课件ppt，共20页。PPT课件主要包含了重点和难点，两直线平行，同位角相等，内错角相等，同旁内角互补，请注意，角的关系，角相等或互补，平行线的性质等内容，欢迎下载使用。
重点：利用平行线的性质解决实际问题。　　　　　　难点：区分平行线的性质与判定方法,以及平行线之间的距离的意义的理解.
1、进一步理解平行线的三条性质；　　　　　　2、学会用平行线的性质,解决一些实际问题；　　　　　　　　　　　　　　3、体会两条平行线之间的距离的意义,学会度量平行线之间的距离；
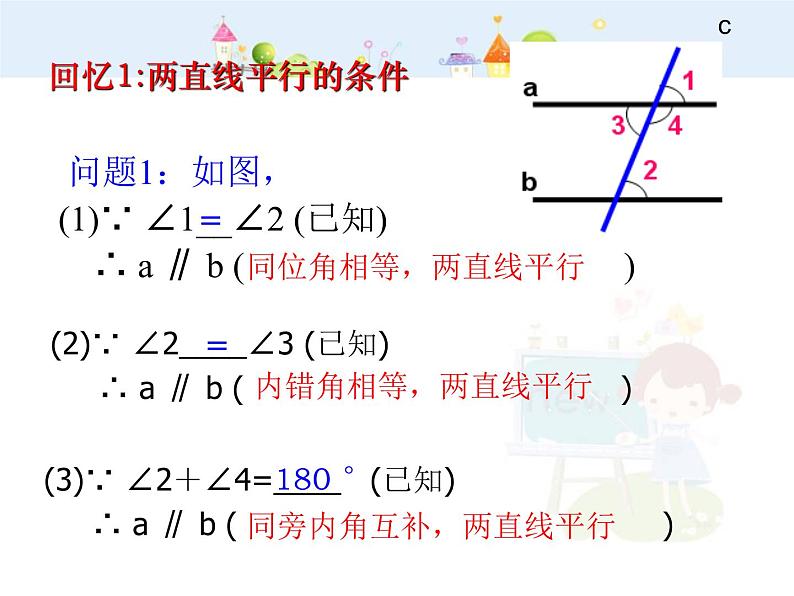
问题1：如图，(1)∵ ∠1__∠2 (已知) ∴ a ∥ b ( )
(2)∵ ∠2____∠3 (已知) ∴ a ∥ b (  )
(3)∵ ∠2＋∠4=____ (已知) ∴ a ∥ b (     )
同位角相等，两直线平行
内错角相等，两直线平行
同旁内角互补，两直线平行
回忆1:两直线平行的条件
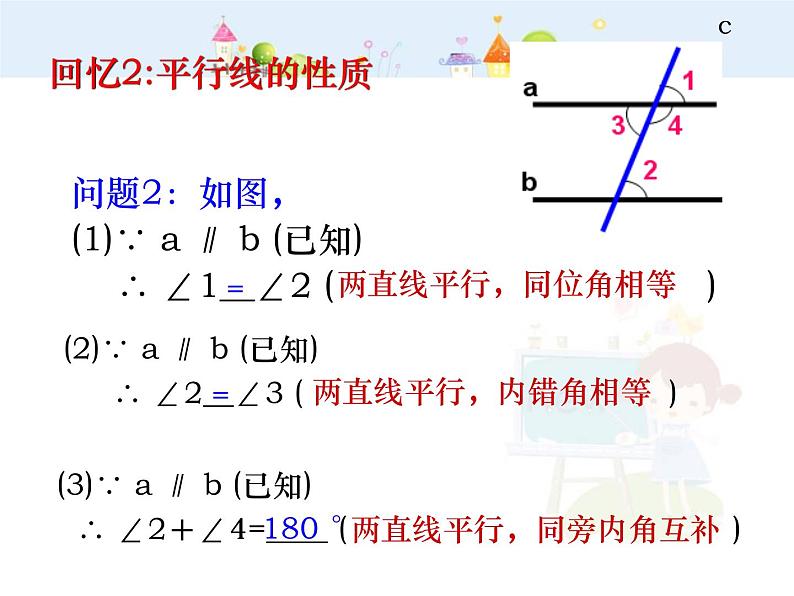
问题2：如图，(1)∵ a ∥ b (已知) ∴ ∠1__∠2 ( )
(2)∵ a ∥ b (已知) ∴ ∠2__∠3 ( )
(3)∵ a ∥ b (已知) ∴ ∠2＋∠4=____ (   )
两直线平行，同位角相等
两直线平行，内错角相等
两直线平行，同旁内角互补
回忆2:平行线的性质
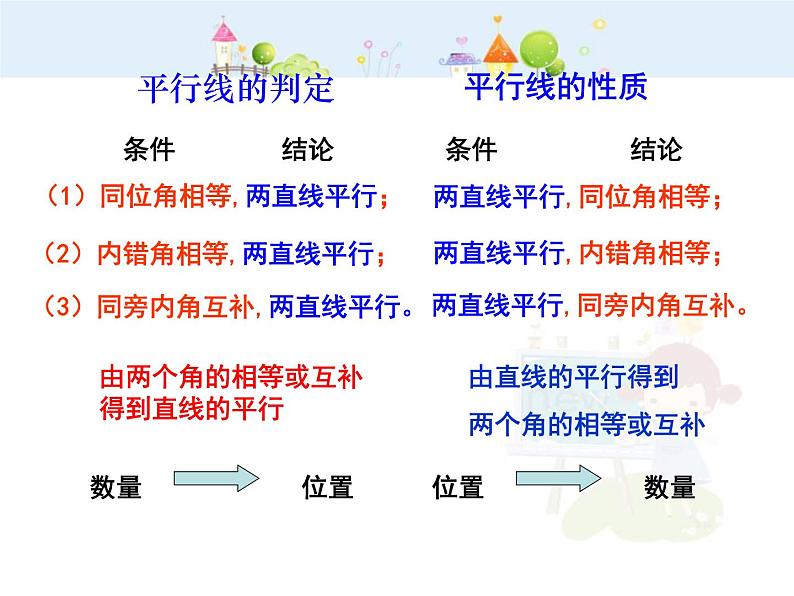
平行线的判定与平行线的性质是因果互换的两类不同的定理，
判定是说：满足了什么条件（性质）的两条直线是互相平行的
性质是说：如果两条直线平行，就应该具有什么性质。
平行线的判定与平行线的性质的比较：
（1）同位角相等,两直线平行；
（2）内错角相等,两直线平行；
（3）同旁内角互补,两直线平行。
两直线平行,同旁内角互补。
两直线平行,同位角相等；
两直线平行,内错角相等；
由两个角的相等或互补得到直线的平行
由直线的平行得到两个角的相等或互补
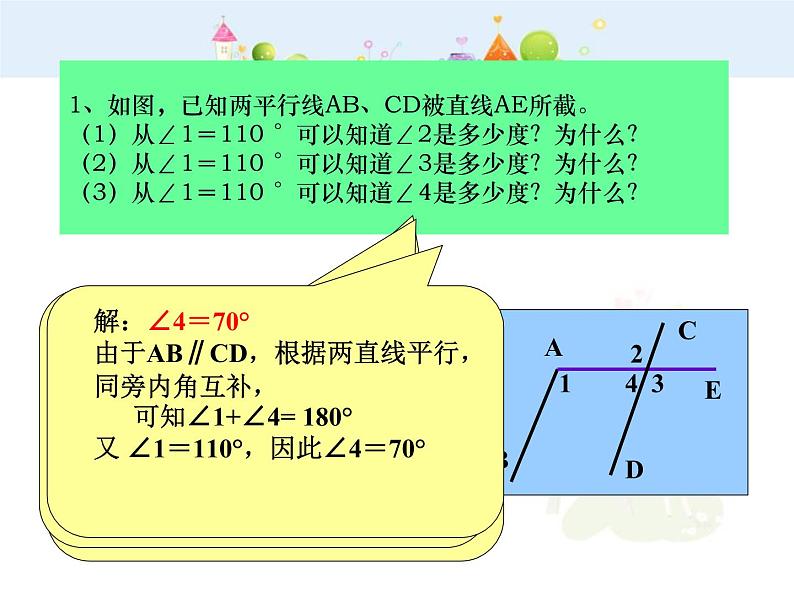
1、如图，已知两平行线AB、CD被直线AE所截。 （1）从∠1＝110 °可以知道∠2是多少度？为什么？ （2）从∠1＝110 °可以知道∠3是多少度？为什么？ （3）从∠1＝110 °可以知道∠4是多少度？为什么？
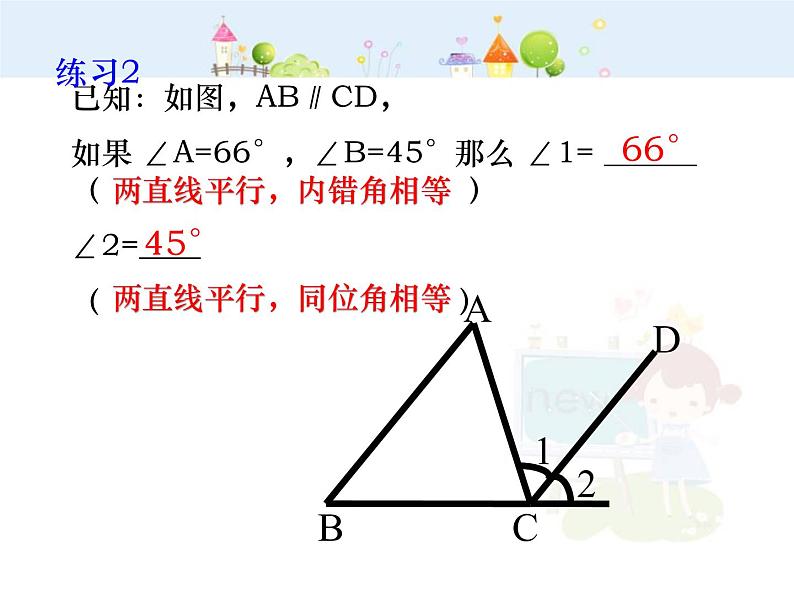
已知：如图，AB∥CD，如果 ∠A=66°，∠B=45°那么 ∠1= ______ （ ） ∠2=____（ ）
4、(1)当______∥______时,∠ABD=∠CDB; (2)当_______∥_______时,∠ADB=∠ CBD; (3)当_______∥_______时,∠BAC=∠DCA; (4)当_______+_______=180°时,AD∥BC (5)当_______∥_______时,∠BAD+∠ADC=180°
3、当AB∥CD时,则下列结论成立的是( )∠DAC=∠ACB (B) ∠DAB+∠ABC=180°
(C)∠ADB=∠DBC (D) ∠BAC=∠ACD
A岛观察B岛，在北偏西35°方向，那么B岛观察A岛的方向是（ ）（A）南偏西55° （B）南偏西35°（C）南偏东35° （D）南偏东55°
宁波到台州的高速公路需开挖山洞，为节约开挖时间，需在山的两面A、B同时开工，在A处测得洞的走向是北偏东75°，那么在B处应按_________方向开工,才能使此洞两边准确接通.
像这样，同时垂直于两条平行线并且夹在这两条平行线间的线段的长度，叫做这两条平行线的距离.
用三角尺和直尺画平行线，做成一张5×5个格子的方格纸.观察做出的方格纸的一部分，线段B1C1,B2C2，…，B5C5都与两条平行的横线A1B5和A2C5垂直吗？它们的长度相等吗？
两点间的距离：连接两点的线段的长度.
点到直线的距离：直线外一点到这条直线的垂线段的长度.
两平行线的距离：夹在两平行线间的垂线段的长度.
如图，如果AB∥CD，在CD上任取一点E，向AB作垂线段EF，这时，EF是否也垂直于直线CD呢？我们这样作出的垂线段EF的长度d是平行线AB、CD的距离吗？
解：过E作EF//AB
所以∠1=∠B=60°
所以∠2=∠D=32°
所以∠BED=∠1+ ∠2 =60°+ 32°= 92°
例1、 已知:如图AB∥CD, ∠ABE= 60°, ∠CDE= 32°,求∠BED的度数.
（同位角相等，两直线平行）
（两直线平行，同位角相等）
（内错角相等，两直线平行）
例2：已知：如图∠1＝∠2， ∠A＝∠C, 说明：AE∥BC
解：因为CE⊥AB， DF⊥AB
所以∠BDF=∠EDF
例3如图，在∆ABC中，CE⊥AB于点E，DF⊥AB于点F，AC//ED，CE是∠ACB的平分线，则∠EDF=∠BDF，请说明理由。
（1）你还能找出图中其他相等的角吗？
（2）反射线BC与EF也平行吗？为什么？
∠1=∠2=∠3=∠4
∠ABH=∠DEH，∠GBC=∠GEF，∠ABC=∠DEF
思考题：如图一束平行光线AB与DE射向一个水平镜面后被反射，此时∠1=∠2，∠3=∠4
1.由___________得到_____________的结论是平行线的判定;
2.由____________得到________________的结论是平行线的性质.