初中数学人教版八年级上册13.1.1 轴对称课前预习课件ppt

这是一份初中数学人教版八年级上册13.1.1 轴对称课前预习课件ppt，共18页。PPT课件主要包含了数学语言，反过来，五角星的对称轴等内容，欢迎下载使用。
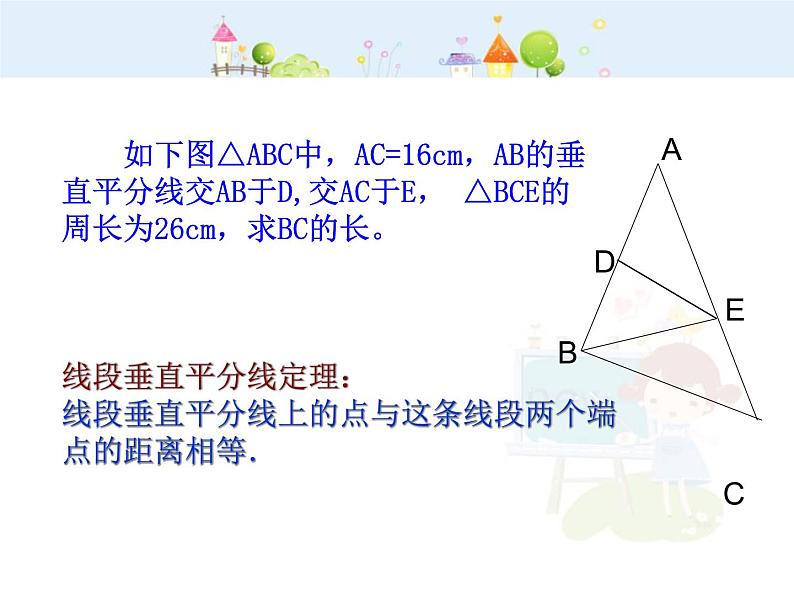
如下图△ABC中，AC=16cm，AB的垂直平分线交AB于D,交AC于E， △BCE的周长为26cm，求BC的长。
线段垂直平分线定理：线段垂直平分线上的点与这条线段两个端点的距离相等．
思考：反过来，如果PA＝PB，那么点P是 否在线段AB的垂直平分线上？
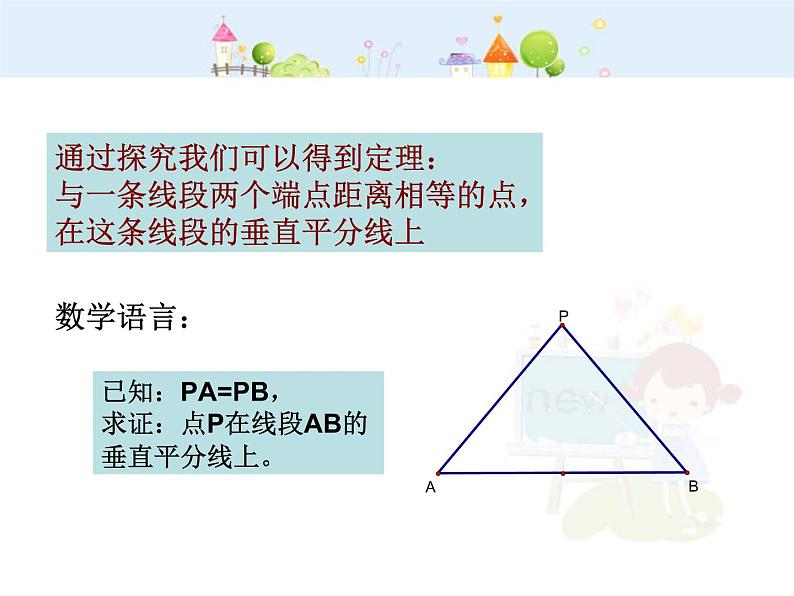
通过探究我们可以得到定理：与一条线段两个端点距离相等的点，在这条线段的垂直平分线上
已知：PA=PB，求证：点P在线段AB的垂直平分线上。
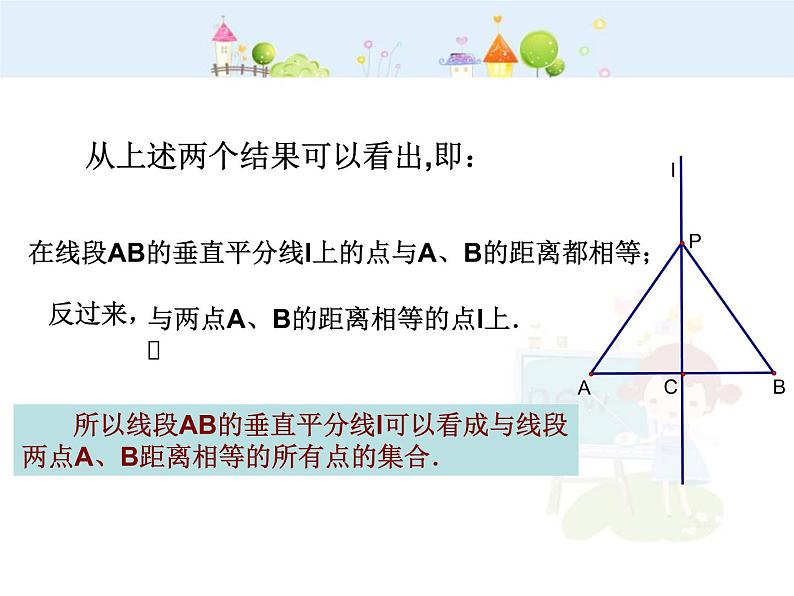
从上述两个结果可以看出,即：
与两点A、B的距离相等的点l上．
在线段AB的垂直平分线l上的点与A、B的距离都相等；
所以线段AB的垂直平分线l可以看成与线段两点A、B距离相等的所有点的集合．
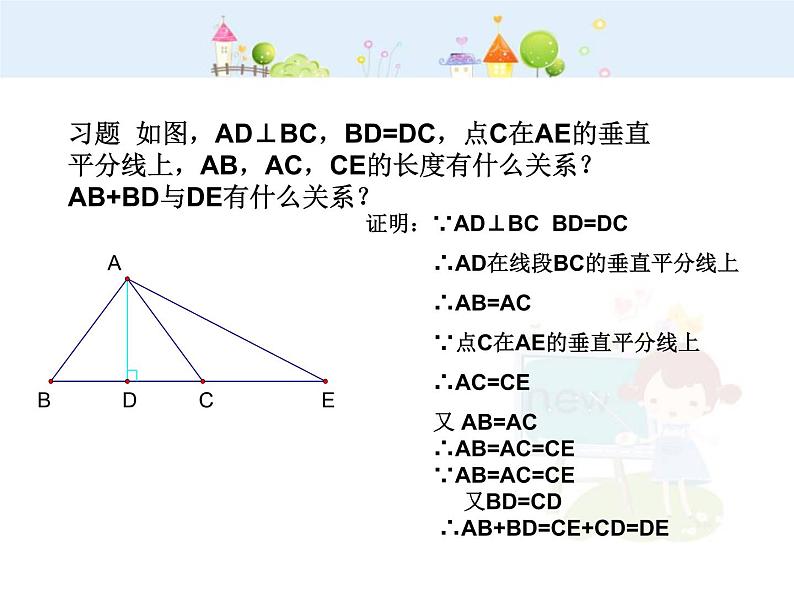
习题 如图，AD⊥BC，BD=DC，点C在AE的垂直平分线上，AB，AC，CE的长度有什么关系？AB+BD与DE有什么关系？
证明：∵AD⊥BC BD=DC ∴AD在线段BC的垂直平分线上 ∴AB=AC ∵点C在AE的垂直平分线上 ∴AC=CE 又 AB=AC ∴AB=AC=CE ∵AB=AC=CE 又BD=CD ∴AB+BD=CE+CD=DE
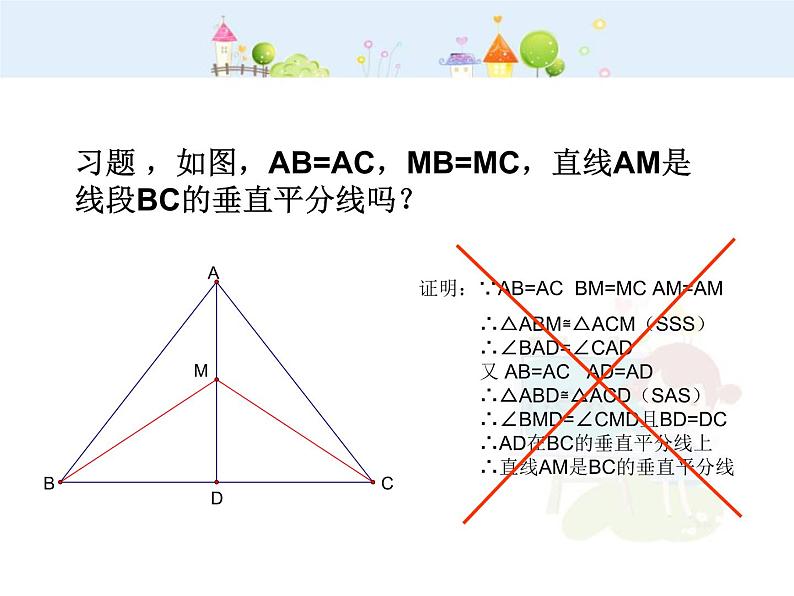
习题 ，如图，AB=AC，MB=MC，直线AM是线段BC的垂直平分线吗？
证明：∵AB=AC BM=MC AM=AM ∴△ABM≌△ACM（SSS） ∴∠BAD=∠CAD 又 AB=AC AD=AD ∴△ABD≌△ACD（SAS） ∴∠BMD=∠CMD且BD=DC ∴AD在BC的垂直平分线上 ∴直线AM是BC的垂直平分线
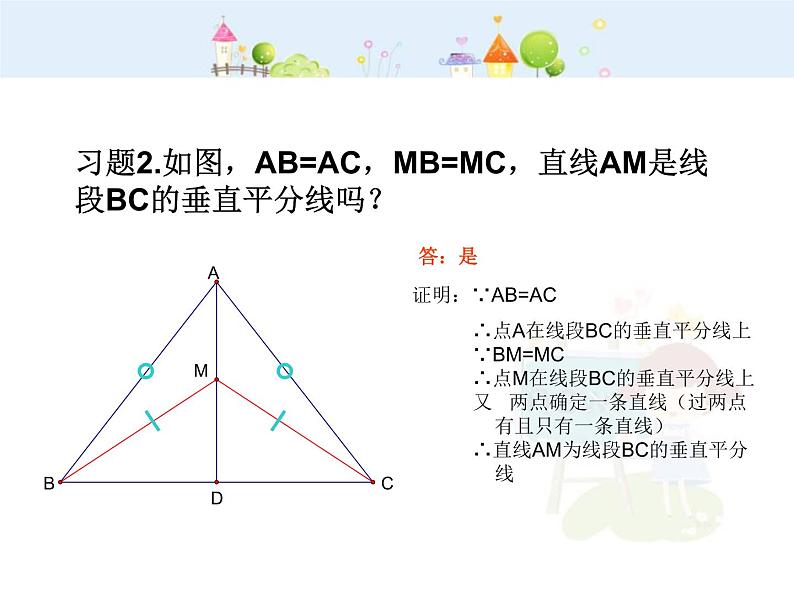
证明：∵AB=AC ∴点A在线段BC的垂直平分线上 ∵BM=MC ∴点M在线段BC的垂直平分线上 又 两点确定一条直线（过两点 有且只有一条直线） ∴直线AM为线段BC的垂直平分 线
习题2.如图，AB=AC，MB=MC，直线AM是线段BC的垂直平分线吗？
例 点A和点B关于某条直线成轴对称，你能作出这条直线吗？
（1）分别以A、B为圆心，以大于 AB的长为半径做弧，两弧相交于C、D两点。
（2）作直线CD，CD即为所求的直线
（3）作直线CD，CD交AB于E，CD即为所求的直线
下列说法：①若直线PE是线段AB的垂直平分线，则EA=EB，PA=PB；②若PA=PB，EA=EB，则直线PE垂直平分线段AB；③若PA=PB，则点P必是线段AB的垂直平分线上的点；④若EA=EB，则过点E的直线垂直平分线段AB．其中正确的个数有（　　）A．1个 B．2个 C．3个 D．4个
4、如图，在Rt△ABC中，∠C=90，DE是AB的垂直平分线，连接AE，∠CAE：∠DAE=1：2，求∠B的度数。
某地有两所大学和两条相交叉的公路OA，OB，现计划修建一个物资仓库，希望仓库到两所大学的距离相等，到两条公路的距离也相等，请你确定该点。
变式训练：某地有两所大学和两条相交叉的公路OA，OB，现计划修建一个物资仓库，希望仓库到两所大学的距离相等，到两条公路的距离也相等，请你确定该点。
如图：请找出一点P，使点P到A，B两点的距离相等，并且点P在∠ACB的平分线上。