

浙教版八年级下册4.4 平行四边形的判定教学课件ppt
展开经历平行四边形判定定理的猜想与证明过程,体会类比思想及探究图形判定的一般思路.
掌握平行四边形的两个判定定理,能根据不同条件灵活选取适当的判定定理进行推理论证.
两组对边分别平行的四边形叫平行四边形.
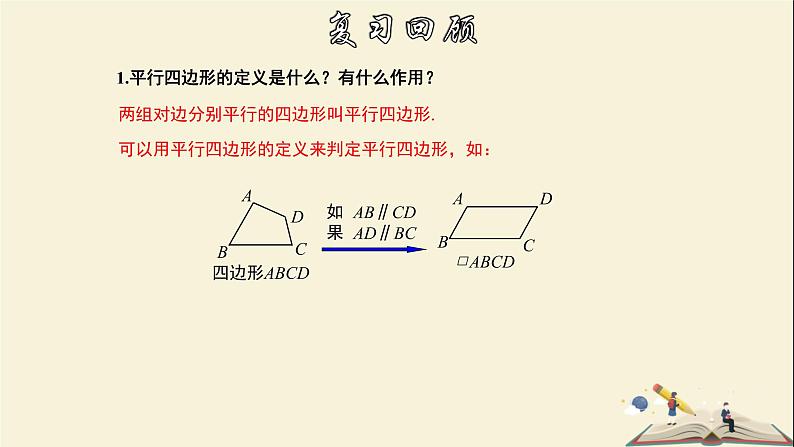
1.平行四边形的定义是什么?有什么作用?
可以用平行四边形的定义来判定平行四边形,如:
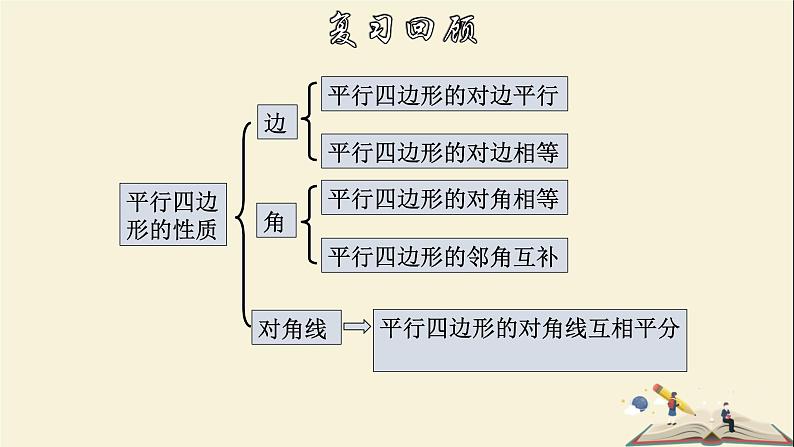
平行四边形的对角线互相平分
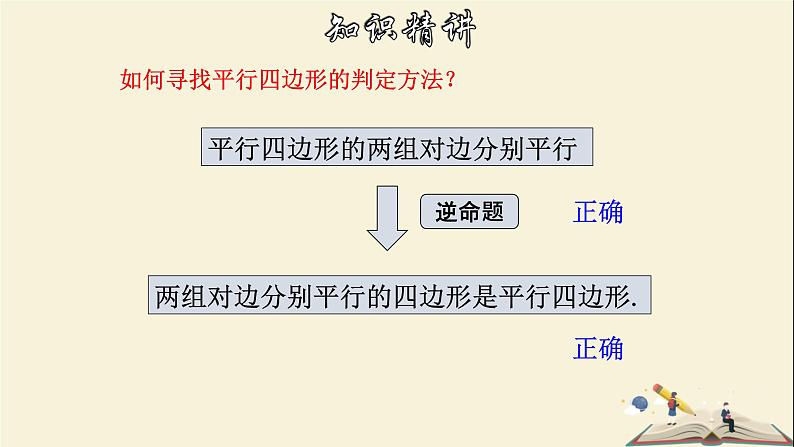
如何寻找平行四边形的判定方法?
平行四边形的两组对边分别平行
两组对边分别平行的四边形是平行四边形.
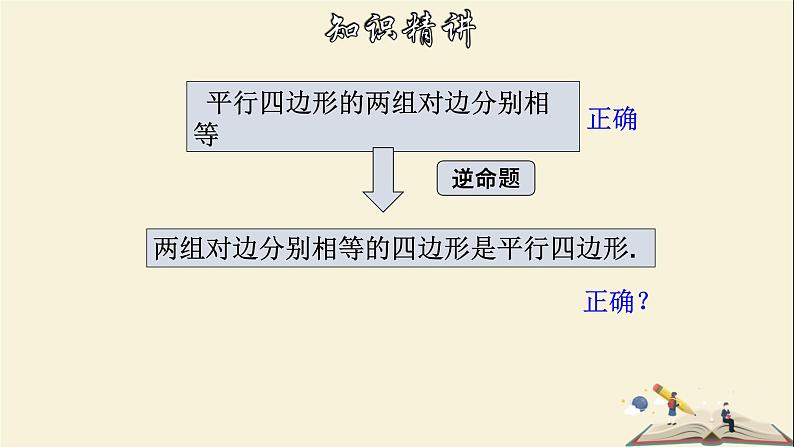
平行四边形的两组对边分别相等
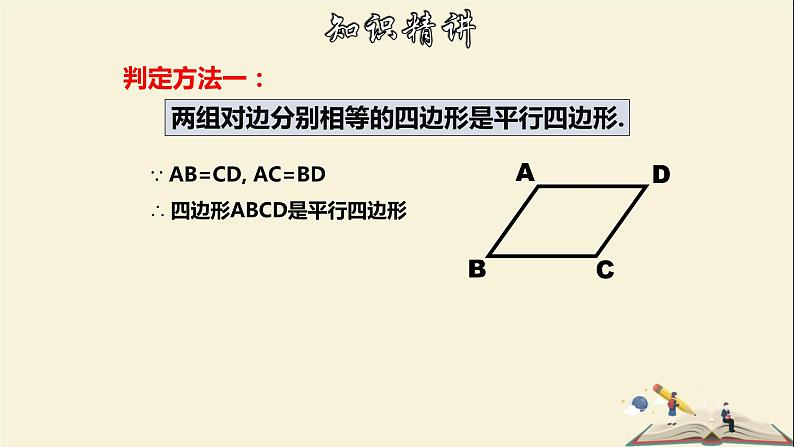
两组对边分别相等的四边形是平行四边形.
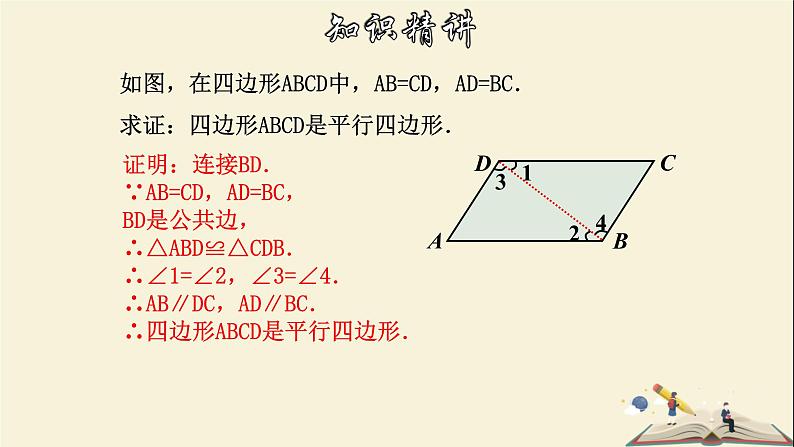
证明:连接BD.∵AB=CD,AD=BC,BD是公共边,∴△ABD≌△CDB.∴∠1=∠2,∠3=∠4.∴AB∥DC,AD∥BC.∴四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.
∵ AB=CD, AC=BD∴ 四边形ABCD是平行四边形
如果仅仅是一组对边平行且相等呢?
一组对边平行且相等的四边形是平行四边形
已知:在四边形ABCD中,AD=BC,AD∥BC.求证:四边形ABCD是平行四边形.
证明:如图,连结BD.∵AD∥BC∴∠ADB=∠CBD(两直线平行,内错角相等)又∵AD=BC,BD=BD∴△ADB≌△CBD (SAS)∴∠ABD=∠CDB(全等三角形的对应角相等)∴AB∥DC(内错角相等,两直线平行)∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
一组对边平行且相等的四边形是平行四边形.
∵ AB∥CD且AB=CD
∴四边形ABCD是平行四边形
思考:一组对边平行,另一组对边相等的四边形是平行四边形吗?
例:梯形的一组对边平行,另一组对边相等,猜想不正确
例1:已知,如图,在□ABCD中,点E、F分别是边AB、CD的中点. 求证:EF//AD
提示:一组对边平行且相等的四边形是平行四边形.
∵四边形ABCD是平行四边形∴AB∥CD且AB=CD∵点E、F分别是边AB、CD的中点∴AE∥DF 且AE=DF∴ 四边形AEFD是平行四边形∴ AD∥EF
已知,四边形ABCD和AEFD都是平行四边形.求证:四边形BCFE是平行四边形.
证明:∵四边形ABCD是平行四边形 ∴AD∥BC且 AD=BC ; 同理AD∥EF且AD=EF ∴ BC∥EF且BC=EF ∴四边形BCFE是平行四边形
的四边形是平行四边形
1.在下列条件中,不能判定四边形是平行四边形的是( )AB∥CD,AD∥BC AB=CD,AD=BC (C)AB∥CD,AB=CD (D) AB∥CD,AD=BC(E) AB∥CD, ∠A=∠C
(一组对边平行且相等)
证明:∵AB=DC,AD=BC,∴四边形ABCD是平行四边形.∴AB∥DC.又∵DC=EF,DE=CF,∴四边形DCFE也是平行四边形.∴DC∥EF.∴AB∥EF.
2.如图,AB=DC=EF,AD=BC,DE=CF.求证:AB∥EF.
3.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
∴AD∥BC且AD=BC
∴△AED ≌ △CFB(SAS)
∴ 四边形BFDE是平行四边形
∵四边形ABCD是平行四边形
4.已知直角坐标系内四个点A(a,1),B(b,1),C(c,-1)D(d,-1).四边形ABCD一定是平行四边形吗?如果你认为是,请给出证明;如果你认为不一定是,请添加一个条件,使他一定是平行四边形.
分析:AB与CD长度不固定,使得AC//BD可能不会成立,所以不一定是平行四边形.
解答:要是四边形一定是平行四边形 则AB=CD 所以,|b-c|=|d-a|
人教版八年级下册18.1.2 平行四边形的判定多媒体教学ppt课件: 这是一份人教版八年级下册18.1.2 平行四边形的判定多媒体教学ppt课件,共20页。PPT课件主要包含了开启记忆之门,平行四边形的对角相等,☆找平行四边形,☆构造平行四边形,当堂检测,画一画,泸州中考题,cm或12cm,数学复习课的主要任务等内容,欢迎下载使用。
浙教版八年级下册第四章 平行四边形4.4 平行四边形的判定课文配套课件ppt: 这是一份浙教版八年级下册第四章 平行四边形4.4 平行四边形的判定课文配套课件ppt,共15页。PPT课件主要包含了学习目标,复习回顾,符号语言,新知学习,猜想是,怎么证明呢,证明连结AC,几何语言,随堂练习,课堂小结等内容,欢迎下载使用。
浙教版八年级下册4.4 平行四边形的判定说课课件ppt: 这是一份浙教版八年级下册4.4 平行四边形的判定说课课件ppt,共26页。PPT课件主要包含了contents,教材分析,教学策略,教学过程,教学感悟,教学目标,教学重难点,教材处理,教材地位,学生学情等内容,欢迎下载使用。













