2020-2021学年4.4 平行四边形的判定教学ppt课件

这是一份2020-2021学年4.4 平行四边形的判定教学ppt课件，共24页。PPT课件主要包含了学习目标，复习回顾，判定方法一，判定方法二，逆命题，知识精讲，∴△AOD≌△COB，∴ADCB，同理ABCD，判定方法三等内容，欢迎下载使用。

掌握平行四边形对角线互相平分的性质.
能灵活运用平行四边形的性质解决具体问题.
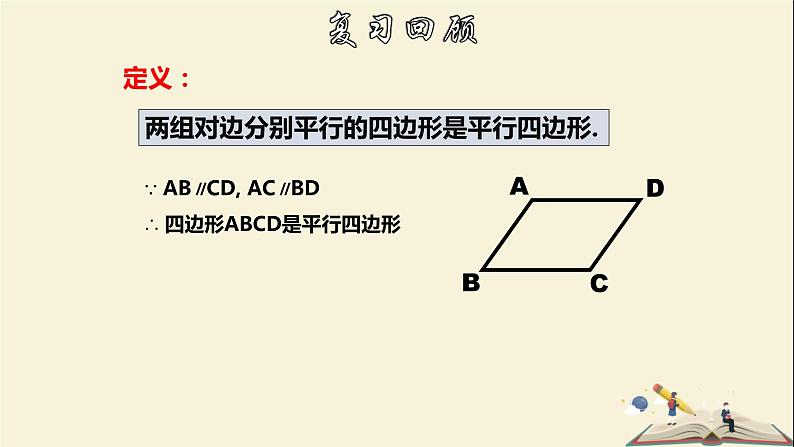
两组对边分别平行的四边形是平行四边形.
∵ AB∥CD, AC∥BD∴ 四边形ABCD是平行四边形
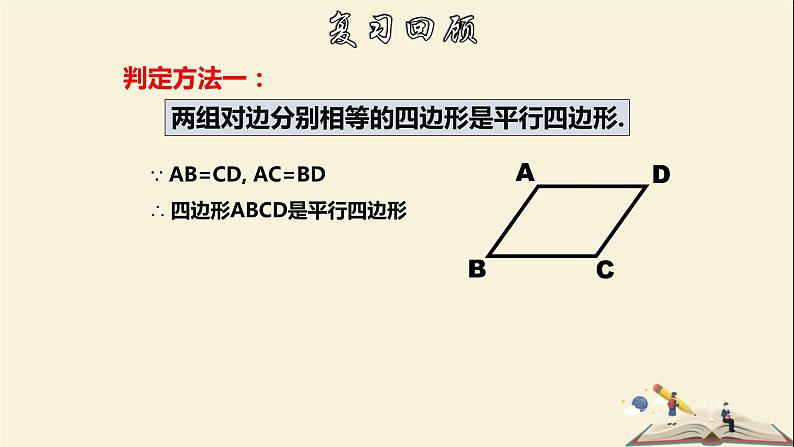
两组对边分别相等的四边形是平行四边形.
∵ AB=CD, AC=BD∴ 四边形ABCD是平行四边形
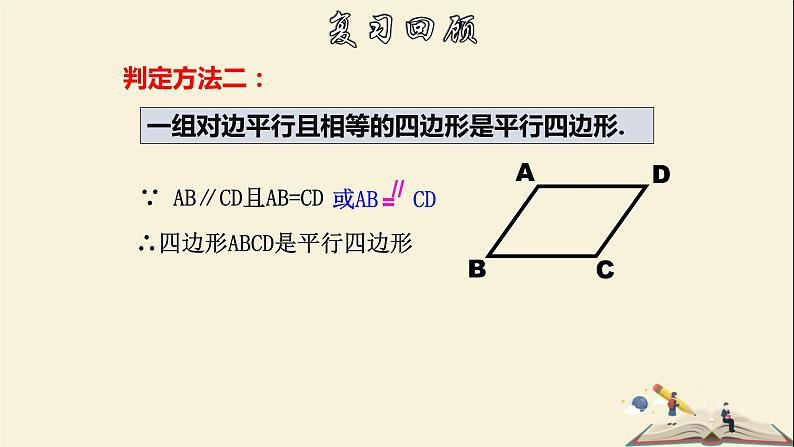
一组对边平行且相等的四边形是平行四边形.
∵ AB∥CD且AB=CD
∴四边形ABCD是平行四边形
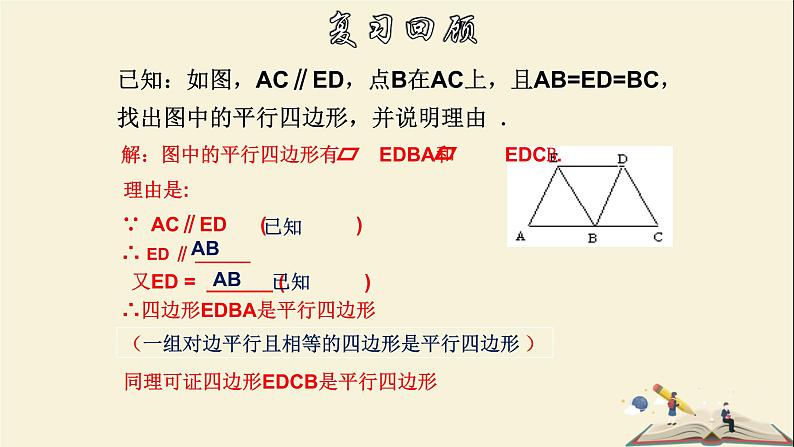
已知：如图，AC∥ED，点B在AC上，且AB=ED=BC， 找出图中的平行四边形，并说明理由 ．
同理可证四边形EDCB是平行四边形
∵ AC∥ED (　 ) ∴ ED ∥ ______ 又ED = ______ (　 )∴四边形EDBA是平行四边形
（一组对边平行且相等的四边形是平行四边形 ）
平行四边形的对角线互相平分
对角线互相平分的四边形是平行四边形.
还有没有其他平行四边形的判定方法呢？
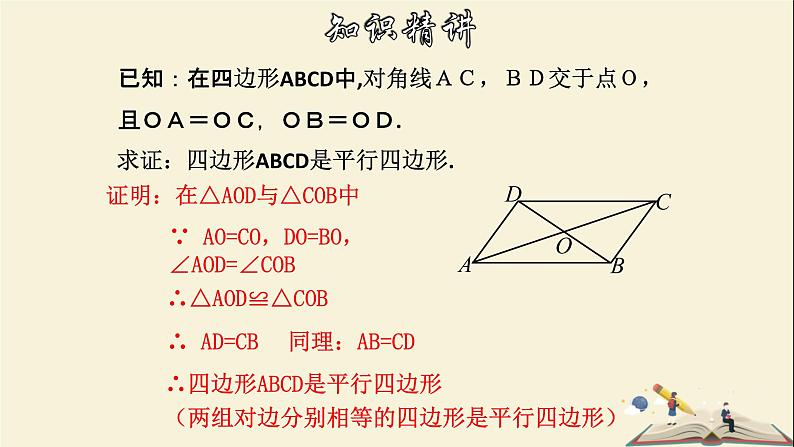
已知：在四边形ABCD中,对角线ＡＣ，ＢＤ交于点Ｏ，且ＯＡ＝ＯＣ，ＯＢ＝ＯＤ.
求证：四边形ABCD是平行四边形.
证明：在△AOD与△COB中
∵ AO=CO，DO=BO，∠AOD=∠COB
（两组对边分别相等的四边形是平行四边形）
∵ AO=OC,OB=OD∴ 四边形ABCD是平行四边形
例:已知如图在 ABCD中，E、F是对角线BD上的两点，且∠BAE=∠DCF.求证：四边形AECF为平行四边形．
证明：连结AC，交BD于点O.在 ABCD中，BO=DO,AO=CO,∵AB∥CD，∴∠ABE=∠CDF.又∵ ∠BAE=∠DCF ，AB=CD,∴△ABE≌ △CDF .∴BE=DF.∴BO-BE=DO-DF,即EO=FO.∴四边形AECF为平行四边形．
1.判断题：⑴相邻的两个角都互补的四边形是平行四边形. (　 )⑵两组对角分别相等的四边形是平行四边形. (　 )⑶一组对边平行，另一组对边相等的四边形是平行四边形 .(　 )⑷一组对边平行且相等的四边形是平行四边形. (　 )⑸对角线相等的四边形是平行四边形. (　 )⑹对角线互相平分的四边形是平行四边形 . ( )
1.两组对边分别平行的四边形是平行四边形(定义)
2.两组对边分别相等的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
两条对角线互相平分的四边形是平行四边形
1.如图，在四边形ABCD中，AC、BD相交于点O，（1）若AD=8cm，AB=4cm，那么当BC=___cm，CD=___cm时，四边形ABCD为平行四边形；（2）若AC=10cm，BD=8cm，那么当AO= cm，DO= cm时，四边形ABCD为平行四边形．
四边形ABCD是不是平行四边形？请给出证明.
∴Ｏ平分ＡＣ，Ｏ平分ＢＤ
连接对角线ＡＣ，ＢＤ则有ＯＡ＝ＯＣ，ＯＢ＝ＯＤ
∴四边形ＡＢＣＤ是平行四边形
3.如图所示，在四边形ABCD中，DC∥AB，以AD，AC为边作□ACED，延长DC交EB于F，求证：EF=FB．
∴四边形BCEG为平行四边形
在□ACED中，AD∥CE，AD=CE
∴CE∥BG，CE=BG
证明：过点B作BG∥AD，交DC的延长线于G，连接EG．∵DC∥AB ∴四边形ABGD是平行四边形∴BG∥AD，BG=AD
4.已知：平行四边形ABCD的对角线AC、BD交于点O，E、F是AC上的两点，并且OE=OF.求证：四边形BFDE是平行四边形
证明： ∵四边形ABCD是平行四边形∴ OB=OD（平行四边形的对角线互相平分）又∵ OE=OF∴ 四边形BFDE是平行四边形
（对角线互相平分的四边形是平行四边形）
5.已知：E、F是平行四边形ABCD对角线AC上的两点，并且AE=CF.求证：四边形BFDE是平行四边形
证明： ∵四边形ABCD是平行四边形∴ OB=OD,OA=OC又∵ AE=FC,∴OE=OF∴ 四边形BFDE是平行四边形
6.已知：E、F是平行四边形ABCD对角线AC上的两点，请你添加一个条件，使得四边形BFDE是平行四边形.
（1）AE=CF（2）AF=CE（3）BE=DF（4）BE∥DF（5）DE=FB（6）DE∥FB (7) ∠DEF= ∠BFE（8）∠DFE= ∠BEF