初中数学浙教版八年级下册5.3 正方形教学ppt课件

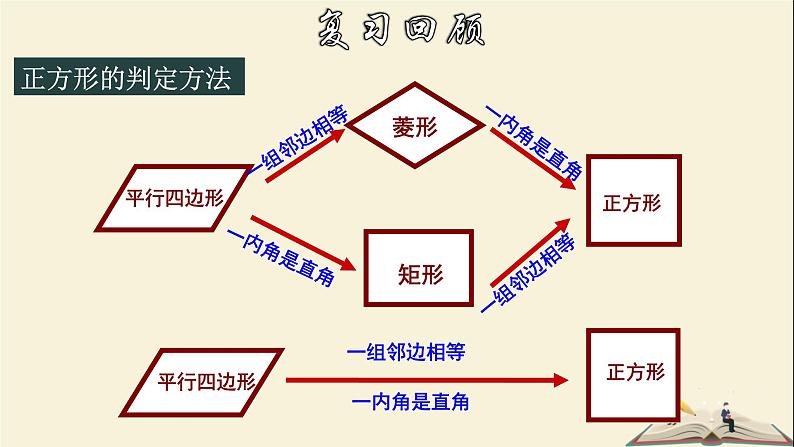
这是一份初中数学浙教版八年级下册5.3 正方形教学ppt课件，共25页。PPT课件主要包含了学习目标，正方形的判定方法，复习回顾，由正方形的定义可知，正方形的性质，知识精讲，平行四边形，针对练习，典例解析，总结提升等内容，欢迎下载使用。
探索并证明正方形的性质，并了解平行四边形、矩形、菱形之间的联系和区别.
会应用正方形的性质解决相关证明及计算问题.
有一组邻边相等且有一个角是直角的平行四边形叫做正方形.
正方形是特殊的平行四边形，也是特殊的矩形，也是特殊的菱形．
菱形的性质+矩形的性质.
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
平行四边形、矩形、菱形、正方形之间关系：
性质：1.正方形的四个角都是直角,四条边相等. 2.正方形的对角线相等且互相垂直平分.
1.一个正方形的面积等于8，则其对角线的长为________.
例1：已知：如图，在正方形ABCD中，G是对角线BD上的一点，GE⊥CD，GF⊥BC，E、F分别为垂足，连结AG，EF.求证：AG=EF
提示：连接CG，下面怎么证明呢？试着证明一下.
∵ GE⊥CD, GF⊥BC
∴ ∠GFC= ∠GEC =90°
（有三个角是直角的四边形是矩形）
又∵ ∠BCD =90°
∴ 四边形FCEG是矩形
在△AGD和△CGD中，∠ADG=∠CDG（正方形的对角线平分一组对角） DG=DG, AD=CD（正方形的四条边相等）
（矩形的两条对角线相等）
例2：在正方形ABCD中，M是正方形内的一点，且MC=MD=AD,求∠BAM的度数？
例3：已知：点E、F、G、H分别是正方形ABCD四条边上的中点，求证：四边形EFGH是正方形.
证明：连接AC、BD，∵四边形ABCD是正方形,∴AC=BD，AC⊥BD，在△ABC中，F. G分别是AB、BC的中点，故可得：FG= AC,同理EH= AC,GH= BD,EF= BD，
在四边形ABCD中，AC=BD，∴EF=FG=GH=HE，∴四边形EFGH是菱形。在△ABD中，E. H分别是AD、CD的中点，则EH∥AC，同理GH∥BD，又∵AC⊥BD，∴EH⊥HG，∴四边形EFGH是正方形.
对边平行，四条边都相等
对角线互相垂直平分且相等，每条对角线平分一组对角
∵四边形ABCD是正方形∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形 中心对称图形
几种特殊四边形的性质
对边平行， 四条边 都相等
对角线互相垂直平分，每条对角线平分一组对角
轴对称图形、中心对称图形
1. 在正方形ABCD的外侧作等边△ADE，则∠AEB的度数为（ ）
A．10° B．12.5° C．15° D．20°
2.在四边形ABCD中，O是对角线的交点，能判定这个四边形是正方形的是（ ）
A．AC=BD，AB∥CD，AB=CDB．AD∥BC，∠A=∠CC．AO=BO=CO=DO，AC⊥BDD．AO=CO，BO=DO，AB=BC
3.如图，在正方形ABCD 中，点E，F 分别是 AB，BC 边上的点，且 AE=BF．求证：CE=DF．
分析：根据正方形的性质可得AB=BC=CD，∠B=∠BCD=90°，然后求出 BE=CF，再利用“SAS”证明△BCE≌△CDF，从而 CF=DF．
证明：在正方形 ABCD 中， AB=BC=CD，∠B=∠BCD=90°. ∵AE=BF， ∴AB-AE=BC-BF，即 BE=CF. 在△BCE 和△CDF 中，BC=CD， ∠B=∠BCD=90°，BE=CF， ∴△BCE≌△CDF（SAS）. ∴CE=DF．
4.已知：如图，正方形ABCD的对角线相交于点O，M、N在OB和OC上，且MN∥BC，连结DN、MC，试猜想DN与MC有什么关系？并证明你的猜想.
又∵MN∥AB∴∠OMN＝∠1＝∠BCO＝∠ONM＝45° ∴OM＝ON
证明：∵四边形ABCD是正方形 ∴OC＝OD , ∠COD=∠COB=90° ∠1＝∠BCO＝45°
∴△COM≌△DON(SAS)
答：DN＝MC DN⊥MC
（2）由△COM≌△DON得∠2=∠3
又∠3+∠CMO=90°
∴∠2+∠CMO=90°
5.如图，正方形ABCD的边长为1cm，AC为对角线，AE平分∠BAC，EF⊥AC，求BE的长．
解：∵四边形ABCD为正方形，∴∠B＝90°，∠ACB＝45°，AB＝BC＝1cm.∵EF⊥AC，∴∠EFA＝∠EFC＝90°.又∵∠ECF＝45°，∴△EFC是等腰直角三角形，∴EF＝FC.∵∠BAE＝∠FAE，∠B＝∠EFA＝90°，AE＝AE，∴△ABE≌△AFE，∴AB＝AF＝1cm，BE＝EF.∴FC＝BE.在Rt△ABC中，∴FC＝AC－AF＝( －1)cm，∴BE＝( －1)cm．
6. 如图在正方形ABCD中,E为CD上一点，F为BC边延长线上一点,且CE=CF. BE与DF之间有怎样的关系？请说明理由.
解：BE=DF,且BE⊥DF.理由如下：∵四边形ABCD是正方形.∴BC=DC,∠BCE =90° .∴∠DCF=180°-∠BCE=90°.∴∠BCE=∠DCF.又∵CE=CF.∴△BCE≌△DCF.∴BE=DF.
延长BE交DE于点M,∵△BCE≌△DCF ,∴∠CBE =∠CDF.∵∠DCF =90° ,∴∠CDF +∠F =90°,∴∠CBE+∠F=90° ,∴∠BMF=90°.∴BE⊥DF.
3.对角线相等且互相垂直平分
有一组邻相等，并且有一个角是直角的平行四边形叫做正方形.