






初中数学人教版七年级下册8.2 消元---解二元一次方程组背景图课件ppt
展开练习1.把方程2(x+3)-3(y-2)=5变形为用含x的式子表示y为 .
2、已知方程组
指出下列方法中比较简捷的解法是( )
A利用①,用含x的式子表示y,再代入②;B利用①,用含y 的式子表示x ,再代入②;C利用②,用含x的式子表示y,再代入①;D利用② ,用含y的式子表示x ,再代入①.
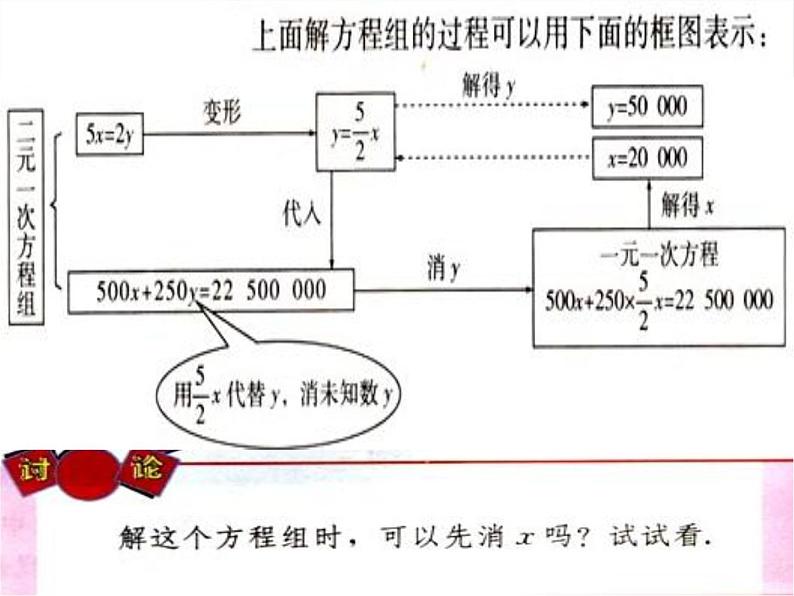
例2根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g),两种产品的销售数量比(按瓶计算)为2:5.某厂每天生产这种消毒液22.5吨,这些消毒液应该分装大、小瓶装两种产品各多少瓶?
解:设这些消毒液应分装x大瓶和y小瓶.由题意,得
解这个方程,得 x= 20000.把x= 20000代入③ ,得 y=50000.所以这个方程组的解是
答:这个工厂一天应生产20000大瓶和50000小瓶消毒液.
大瓶所装消毒液+小瓶所装消毒液=总生产量
解:设有x支篮球队和y支排球队参赛.由题意,得
由①, 得 y =48- x ③把③代入②,得 10x+12(48-x)=520解这个方程,得 x= 28.把x= 28代入③ ,得 y=20.所以这个方程组的解是
解:设骑车用x小时,步行用y小时.由题意,得
由①, 得 y =1- x ③把③代入②,得 25x+5(1-x)=20
昨天,我们一家8个人去公园玩,买门票花了34元。
哦,那你们家去了几个大人?几个小孩呢?
真笨,自已不会算吗?成人票5元每人,小孩3元每人啊!
聪明的同学们,你能帮他算算吗?
解:设有x个成人,y个儿童,由 此可列方程组 .
例:已知:方程组 甲由于看错了a,解得 乙看了错b解得 , 求原方程组正确的解
1.用代入法解方程组:
2①已知方程组 的解为
②求满足5x+3y=x+2y=7的x,y的值.
3.一个三位数,三个数位上的数字和是11。如果把百位上的数字与个位上的数字对调,那么所成的数比原数大693;如果把十位上的数字与个位上的数字对调,那么所成的数比原数少54,求这个三位数。
1.解下列二元一次方程组
你认为怎样代入更简便?
请用你最简便的方法解出它的解。
你的思路能解另一题吗?
x+1=2(y-1)3(x+1)=5(y-1)+4
1.解下列二元一次方程组(分组练习)
可将(x+1)、(y-1)看作一个整体求解。
3×2(y-1)= 5(y-1) + 4
6(y-1) =5(y-1)+4
(y-1) = 4 ③
3x+2y=133x - 2y = 5
解下列二元一次方程组(分组练习)
可将2y看作一个数来求解。
3x + (3x – 5) = 13
把x = 3 代入③
2y = 9 – 5
2y = 3x – 5 ③
用整体代入法解方程组:
1,已知x=t-2,y=2t+1,用含x的式子表示y: .用含y的式子表示x: .
2,若方程组 的解x与y相等,则a的值等于( )A.4 B.10 C.11 D.12
3x + 2(2x – 3)= 8
3x + 4x – 6 = 8
3x + 4x = 8 + 6
把x = 2 代入③,得:
4、如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.
5x + 2(2 – 3x)- 2 = 0
5x + 4 – 6x – 2 = 0
5x – 6x = 2 - 4
答:x 的值是2,y 的值是-4.
如果把这两个方程的左边与左边相减,右边与右边相减,能得到什么结果?
左边与左边相减所得到的代数式和右边与右边相减所得到的代数式有什么关系?
将y=-2代入①,得:
分析:可以发现7y与-7y互为相反数,若把两个方程的左边与左边相加,右边与右边相加,就可以消去未知数y
用什么方法可以消去一个未知数?先消去哪一个比较方便?
通过将两个方程相加(或相减)消去一个未知数,将方程组转化为一元一次方程来解的解法叫做加减消元法,简称加减法。
当同一个未知数的系数相同时,用减法;当同一个未知数的系数互为相反数时,用加法。
人教版七年级下册8.2 消元---解二元一次方程组教课ppt课件: 这是一份人教版七年级下册8.2 消元---解二元一次方程组教课ppt课件,共23页。PPT课件主要包含了知识回顾,例题分析,这节课你有哪些收获,归纳总结等内容,欢迎下载使用。
初中数学人教版七年级下册第八章 二元一次方程组8.2 消元---解二元一次方程组示范课课件ppt: 这是一份初中数学人教版七年级下册第八章 二元一次方程组8.2 消元---解二元一次方程组示范课课件ppt,共7页。PPT课件主要包含了x5y2,例题5等内容,欢迎下载使用。
湘教版七年级下册1.2.1 代入消元法授课ppt课件: 这是一份湘教版七年级下册1.2.1 代入消元法授课ppt课件,共13页。PPT课件主要包含了由①我们可以得到,再将②中的y换为,就得到了③,解设胜x场则有,请同学们读一读,例1在实践中学习,随堂练习,y2x,x+y12,y-5等内容,欢迎下载使用。













