八年级上期末数学试卷09（教培机构期末复习模拟专用）

这是一份八年级上期末数学试卷09（教培机构期末复习模拟专用），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
八年级（上）期末数学试卷
　
一、选择题（每小题3分，共30分）
1．下列计算正确的是（　　）
A．a2•a3=a6 B．2a•3a=6a C．（a2）3=a6 D．（a+b）2=a2+b2
2．如果三角形的两边长分别为3和5，第三边长是偶数，则第三边长可以是（　　）
A．2 B．3 C．4 D．8
3．已知点A（m﹣1，3）与点B（2，n+1）关于x轴对称，则m+n的值为（　　）
A．﹣1 B．﹣7 C．1 D．7
4．已知图中的两个三角形全等，则∠α的度数是（　　）

A．72° B．60° C．58° D．50°
5．化简的结果是（　　）
A． B． C． D．a+b
6．如图所示，在△ABC中，∠B=47°，∠C=23°，AD是△ABC的角平分线，则∠CAD的度数为（　　）

A．40° B．45° C．50° D．55°
7．在x2﹣y2，﹣x2+y2，（﹣x）2+（﹣y）2，x4﹣y2中能用平方差公式分解因式的有（　　）
A．1个 B．2个 C．3个 D．4个
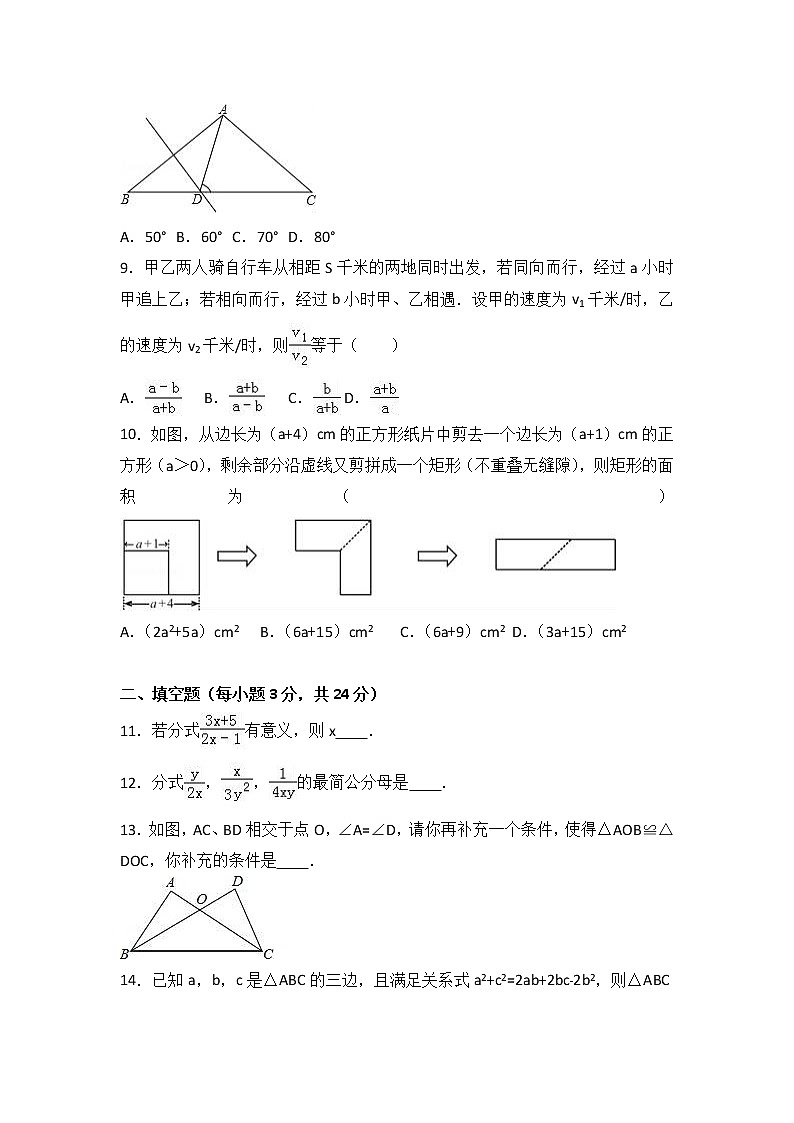
8．如图，AB=AC，∠BAC=110°，AB的垂直平分线交BC于点D，那么∠ADC=（　　）

A．50° B．60° C．70° D．80°
9．甲乙两人骑自行车从相距S千米的两地同时出发，若同向而行，经过a小时甲追上乙；若相向而行，经过b小时甲、乙相遇．设甲的速度为v1千米/时，乙的速度为v2千米/时，则等于（　　）
A． B． C． D．
10．如图，从边长为（a+4）cm的正方形纸片中剪去一个边长为（a+1）cm的正方形（a＞0），剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则矩形的面积为（　　）
A．（2a2+5a）cm2 B．（6a+15）cm2 C．（6a+9）cm2 D．（3a+15）cm2
　
二、填空题（每小题3分，共24分）
11．若分式有意义，则x　　．
12．分式，，的最简公分母是　　．
13．如图，AC、BD相交于点O，∠A=∠D，请你再补充一个条件，使得△AOB≌△DOC，你补充的条件是　　．

14．已知a，b，c是△ABC的三边，且满足关系式a2+c2=2ab+2bc﹣2b2，则△ABC是　　三角形．
15．若x2+y2=10，xy=﹣3，则（x+y）2=　　．
16．若关于x的方程无解，则m=　　．
17．如图，△ABC的周长为22cm，∠ABC，∠ACB的平分线交于O，OD⊥BC于D，且OD=3cm，则△ABC的面积为　　cm2．

18．如图，P为△ABC内的一点，D、E、F分别是点P关于边AB、BC、CA所在直线的对称点，那么∠ADB+∠BEC+CFA等于　　．

　
三、解答题（本题共7小题，满分66分）
19．（1）分解因式：（p﹣4）（p+1）+3p；
（2）计算：8（x+2）2﹣（3x﹣1）（3x+1）．
20．设A=，B=+1，当x为何值时，A与B的值相等．
21．先化简（1﹣）÷，再从0，﹣2，﹣1，1中选择一个合适的数代入并求值．
22．如图所示，一个四边形纸片ABCD，∠B=∠D=90°，把纸片按如图所示折叠，使点B落在AD边上的B′点，AE是折痕．
（1）试判断B′E与DC的位置关系；
（2）如果∠C=130°，求∠AEB的度数．

23．如图，已知AB=CD，∠B=∠C，AC和BD相交于点O，E是AD的中点，连接OE．
（1）求证：△AOB≌△DOC；
（2）求∠AEO的度数．

24．某商家预测一种应季衬衫能畅销市场，就用13200元购进了一批这种衬衫，面市后果然供不应求，商家又用28800元购进了第二批这种衬衫，所购数量是第一批购进量的2倍，但单价贵了10元．
（1）该商家购进的第一批衬衫是多少件？
（2）若两批衬衫按相同的标价销售，最后剩下50件按八折优惠卖出，如果两批衬衫全部售完后利润不低于25%（不考虑其他因素），那么每件衬衫的标价至少是多少元？
25．已知：如图，△ABC为等边三角形，过AB边上的点D作DG∥BC，交AC于G，在GD的延长线上取点E，使DE=DB，连接AE，CD．
（1）求证：△AGE≌△DAC；
（2）把线段DC沿DE方向向左平移，当D平移至点E的位置时，点C恰好与线段BC上的点F重合（如图），请连接AF，并判断△AEF是怎样的三角形，试证明你的结论．

　

八年级（上）期末数学试卷
参考答案与试题解析
　
一、选择题（每小题3分，共30分）
1．下列计算正确的是（　　）
A．a2•a3=a6 B．2a•3a=6a C．（a2）3=a6 D．（a+b）2=a2+b2
【考点】整式的混合运算．
【分析】根据同底数幂的乘法、单项式乘以单项式、幂的乘方、完全平方公式分别求出每个式子的值，再判断即可．
【解答】解：A、结果是a5，故本选项错误；
B、结果是6a2，故本选项错误；
C、结果是a6，故本选项正确；
D、结果是a2+2ab+b2，故本选项错误；
故选C．
　
2．如果三角形的两边长分别为3和5，第三边长是偶数，则第三边长可以是（　　）
A．2 B．3 C．4 D．8
【考点】三角形三边关系．
【分析】根据三角形三边关系，可令第三边为X，则5﹣3＜X＜5+3，即2＜X＜8，又因为第三边长为偶数，所以第三边长是4，6．问题可求．
【解答】解：由题意，令第三边为X，则5﹣3＜X＜5+3，即2＜X＜8，
∵第三边长为偶数，∴第三边长是4或6．
∴三角形的第三边长可以为4．
故选C．
　
3．已知点A（m﹣1，3）与点B（2，n+1）关于x轴对称，则m+n的值为（　　）
A．﹣1 B．﹣7 C．1 D．7
【考点】关于x轴、y轴对称的点的坐标．
【分析】本题比较容易，考查平面直角坐标系中两个关于坐标轴成轴对称的点的坐标特点：关于y轴对称的点，纵坐标相同，横坐标互为相反数．
【解答】解：∵点A（m﹣1，3）与点B（2，n+1）关于x轴对称，
∴，
∴，
∴m+n=3+（﹣4）=﹣1．
故选A．
　
4．已知图中的两个三角形全等，则∠α的度数是（　　）

A．72° B．60° C．58° D．50°
【考点】全等三角形的性质．
【分析】根据全等三角形对应角相等可知∠α是b、c边的夹角，然后写出即可．
【解答】解：∵两个三角形全等，
∴∠α的度数是72°．
故选A．
　
5．化简的结果是（　　）
A． B． C． D．a+b
【考点】分式的加减法．
【分析】异分母的分式相加减，先将分母分解因式，再通分、化简即可．
【解答】解：
=
=．
故选A．
　
6．如图所示，在△ABC中，∠B=47°，∠C=23°，AD是△ABC的角平分线，则∠CAD的度数为（　　）

A．40° B．45° C．50° D．55°
【考点】三角形内角和定理．
【分析】根据三角形内角和定理求出∠BAC，根据角平分线的定义计算即可．
【解答】解：∵∠B=47°，∠C=23°，
∴∠BAC=180°﹣∠B﹣∠C=110°，
∵AD是△ABC的角平分线，
∴∠CAD=∠BAC=55°，
故选：D．
　
7．在x2﹣y2，﹣x2+y2，（﹣x）2+（﹣y）2，x4﹣y2中能用平方差公式分解因式的有（　　）
A．1个 B．2个 C．3个 D．4个
【考点】因式分解-运用公式法．
【分析】利用平方差公式的结构特征判断即可．
【解答】解：在x2﹣y2，能；﹣x2+y2，能；（﹣x）2+（﹣y）2，不能；x4﹣y2，能，
则能用平方差公式分解因式的有3个，
故选C
　
8．如图，AB=AC，∠BAC=110°，AB的垂直平分线交BC于点D，那么∠ADC=（　　）

A．50° B．60° C．70° D．80°
【考点】等腰三角形的性质；线段垂直平分线的性质．
【分析】先根据等腰三角形内角和定理得出∠B的度数，再由中垂线的知识得出△ABD为等腰直角三角形，可得出∠BAD的度数，根据三角形的一个外角等于与其不相邻的两内角和，即可得出∠ADC的度数．
【解答】解：根据题意，在△ABC中，AB=AC，∠BAC=110°，
∴∠B=35°，
又AB的垂直平分线交BC于点D，
∴∠BAD=∠B=35°，
在△BAD中，∠ADC=∠B+∠BAD=70°，
∴∠ADC=70°．
故答案选C．
　
9．甲乙两人骑自行车从相距S千米的两地同时出发，若同向而行，经过a小时甲追上乙；若相向而行，经过b小时甲、乙相遇．设甲的速度为v1千米/时，乙的速度为v2千米/时，则等于（　　）
A． B． C． D．
【考点】列代数式（分式）．
【分析】根据题意得到a（v1﹣v2）=s，①，b（v1+v2）=s，②，由①②，解得v1，v2，即可求出答案．
【解答】解：a（v1﹣v2）=s，①，b（v1+v2）=s，②，
由①②，解得v1=，v2=，
=，
故选B
　
10．如图，从边长为（a+4）cm的正方形纸片中剪去一个边长为（a+1）cm的正方形（a＞0），剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则矩形的面积为（　　）
A．（2a2+5a）cm2 B．（6a+15）cm2 C．（6a+9）cm2 D．（3a+15）cm2
【考点】平方差公式的几何背景．
【分析】大正方形与小正方形的面积的差就是矩形的面积，据此即可求解．
【解答】解：矩形的面积是：（a+4）2﹣（a+1）2
=（a+4+a+1）（a+4﹣a﹣1）
=3（2a+5）
=6a+15（cm2）．
故选B．
　
二、填空题（每小题3分，共24分）
11．若分式有意义，则x　　．
【考点】分式有意义的条件．
【分析】根据分式有意义的条件可得2x﹣1≠0，再解即可．
【解答】解：由题意得：2x﹣1≠0，
解得：x≠，
故答案为：．
　
12．分式，，的最简公分母是　12xy2　．
【考点】最简公分母．
【分析】确定最简公分母的方法是：
（1）取各分母系数的最小公倍数；
（2）凡单独出现的字母连同它的指数作为最简公分母的一个因式；
（3）同底数幂取次数最高的，得到的因式的积就是最简公分母．
【解答】解：分式，，的分母分别是2x、3y2、4xy，故最简公分母是12xy2．
故答案为12xy2．
　
13．如图，AC、BD相交于点O，∠A=∠D，请你再补充一个条件，使得△AOB≌△DOC，你补充的条件是　AO=DO或AB=DC或BO=CO　．

【考点】全等三角形的判定．
【分析】本题要判定△AOB≌△DOC，已知∠A=∠D，∠AOB=∠DOC，则可以添加AO=DO或AB=DC或BO=CO从而利用ASA或AAS判定其全等．
【解答】解：添加AO=DO或AB=DC或BO=CO后可分别根据ASA、AAS、AAS判定△AOB≌△DOC．
故填AO=DO或AB=DC或BO=CO．
　
14．已知a，b，c是△ABC的三边，且满足关系式a2+c2=2ab+2bc﹣2b2，则△ABC是　等边　三角形．
【考点】因式分解的应用．
【分析】先把原式化为完全平方的形式再求解．
【解答】解：∵原式=a2+c2﹣2ab﹣2bc+2b2=0，
a2+b2﹣2ab+c2﹣2bc+b2=0，
即（a﹣b）2+（b﹣c）2=0，
∴a﹣b=0且b﹣c=0，即a=b且b=c，
∴a=b=c．
故△ABC是等边三角形．
故答案为：等边．
　
15．若x2+y2=10，xy=﹣3，则（x+y）2=　94　．
【考点】完全平方公式．
【分析】根据∴（x+y）2=x2+2xy+y2，代入计算即可．
【解答】解：∵x2+y2=10，xy=﹣3，
∴（x+y）2=x2+2xy+y2=100﹣6=94；
故答案为：94．
　
16．若关于x的方程无解，则m=　﹣2　．
【考点】分式方程的解．
【分析】分式方程无解的条件是：去分母后所得整式方程无解，或解这个整式方程得到的解使原方程的分母等于0．
【解答】解：去分母得：2=x﹣3﹣m，
解得：x=5+m，
当分母x﹣3=0即x=3时方程无解，
∴5+m=3即m=﹣2时方程无解，则m=﹣2．
故答案为：﹣2．
　
17．如图，△ABC的周长为22cm，∠ABC，∠ACB的平分线交于O，OD⊥BC于D，且OD=3cm，则△ABC的面积为　33　cm2．

【考点】角平分线的性质．
【分析】过点O作OE⊥AB于E，OF⊥AC于F，然后根据角平分线上的点到角的两边的距离相等的性质可得OD=OE=OF，再根据三角形面积计算即可得解．
【解答】解：如图，过点O作OE⊥AB于E，OF⊥AC于F，
∵∠ABC、∠ACB的平分线，OD⊥BC，
∴OD=OE，OD=OF，
∴OD=OE=OF=3cm，
∴△ABC的面积=（AB+BC+AC）×3=33cm2；
故答案为：33．

　
18．如图，P为△ABC内的一点，D、E、F分别是点P关于边AB、BC、CA所在直线的对称点，那么∠ADB+∠BEC+CFA等于　360°　．

【考点】轴对称的性质．
【分析】连接PA、PB、PC，根据轴对称的性质可得∠DAB=∠PAB，∠FAC=∠PAC，从而求出∠DAF=2∠BAC，同理可求∠DBE=2∠ABC，∠ECF=2∠ACB，再根据六边形的内角和定理列式计算即可得解．
【解答】解：如图，连接PA、PB、PC，
∵D、F分别是点P关于边AB、CA所在直线的对称点，
∴∠DAB=∠PAB，∠FAC=∠PAC，
∴∠DAF=2∠BAC，
同理可求∠DBE=2∠ABC，∠ECF=2∠ACB，
∵∠BAC+∠ABC+∠ACB=180°，
∴∠DAF+∠DBE+∠ECF=180°×2=360°，
∴∠ADB+∠BEC+CFA=（6﹣2）•180°﹣（∠DAF+∠DBE+∠ECF）=720°﹣360°=360°．
故答案为：360°．

　
三、解答题（本题共7小题，满分66分）
19．（1）分解因式：（p﹣4）（p+1）+3p；
（2）计算：8（x+2）2﹣（3x﹣1）（3x+1）．
【考点】整式的混合运算．
【分析】（1）原式整理后，利用平方差公式分解即可；
（2）原式利用平方差公式及完全平方公式化简即可得到结果．
【解答】解：（1）原式=p2﹣3p﹣4+3p=p2﹣4=（p+2）（p﹣2）；
（2）原式=8x2+32x+32﹣9x2+1=﹣x2+32x+33．
　
20．设A=，B=+1，当x为何值时，A与B的值相等．
【考点】解分式方程．
【分析】A与B的值相等，让两个代数式相等，化为分式方程求解．
【解答】解：当A=B时， =+1，
=+1，
方程两边同时乘以（x+1）（x﹣1），
得x（x+1）=3+（x+1）（x﹣1），
x+x=3+x﹣1，
∴x=2．
检验，当x=2时，（x+1）（x﹣1）=3≠0．
∴x=2是分式方程的根．
因此，当x=2时，A=B．
　
21．先化简（1﹣）÷，再从0，﹣2，﹣1，1中选择一个合适的数代入并求值．
【考点】分式的化简求值．
【分析】先把分式的分子和分母因式分解，并且把除法运算转化为乘法运算得到原式=•，约分后得到原式=，由于x不能取±1，2，所以可以把x=0代入计算．
【解答】解：原式=•
=，
当x=0时，原式==﹣．
　
22．如图所示，一个四边形纸片ABCD，∠B=∠D=90°，把纸片按如图所示折叠，使点B落在AD边上的B′点，AE是折痕．
（1）试判断B′E与DC的位置关系；
（2）如果∠C=130°，求∠AEB的度数．

【考点】全等三角形的判定与性质．
【分析】（1）由于AB′是AB的折叠后形成的，所以∠AB′E=∠B=∠D=90°，∴B′E∥DC；
（2）利用平行线的性质和全等三角形求解．
【解答】解：（1）由于AB′是AB的折叠后形成的，
∠AB′E=∠B=∠D=90°，
∴B′E∥DC；

（2）∵折叠，
∴△ABE≌△AB′E，
∴∠AEB′=∠AEB，即∠AEB=∠BEB′，
∵B′E∥DC，∴∠BEB′=∠C=130°，
∴∠AEB=∠BEB′=65°．
　
23．如图，已知AB=CD，∠B=∠C，AC和BD相交于点O，E是AD的中点，连接OE．
（1）求证：△AOB≌△DOC；
（2）求∠AEO的度数．

【考点】全等三角形的判定．
【分析】（1）由已知可以利用AAS来判定其全等；
（2）再根据等腰三角形三线合一的性质即可求得其为直角．
【解答】（1）证明：在△AOB和△DOC中
∵
∴△AOB≌△DOC（AAS）

（2）解：∵△AOB≌△DOC，
∴AO=DO
∵E是AD的中点
∴OE⊥AD
∴∠AEO=90°
　
24．某商家预测一种应季衬衫能畅销市场，就用13200元购进了一批这种衬衫，面市后果然供不应求，商家又用28800元购进了第二批这种衬衫，所购数量是第一批购进量的2倍，但单价贵了10元．
（1）该商家购进的第一批衬衫是多少件？
（2）若两批衬衫按相同的标价销售，最后剩下50件按八折优惠卖出，如果两批衬衫全部售完后利润不低于25%（不考虑其他因素），那么每件衬衫的标价至少是多少元？
【考点】分式方程的应用；一元一次不等式的应用．
【分析】（1）可设该商家购进的第一批衬衫是x件，则购进第二批这种衬衫是2x件，根据第二批这种衬衫单价贵了10元，列出方程求解即可；
（2）设每件衬衫的标价y元，求出利润表达式，然后列不等式解答．
【解答】解：（1）设该商家购进的第一批衬衫是x件，则购进第二批这种衬衫是2x件，依题意有
+10=，
解得x=120，
经检验，x=120是原方程的解，且符合题意．
答：该商家购进的第一批衬衫是120件．

（2）3x=3×120=360，
设每件衬衫的标价y元，依题意有
y+50×0.8y≥×（1+25%），
解得y≥150．
答：每件衬衫的标价至少是150元．
　
25．已知：如图，△ABC为等边三角形，过AB边上的点D作DG∥BC，交AC于G，在GD的延长线上取点E，使DE=DB，连接AE，CD．
（1）求证：△AGE≌△DAC；
（2）把线段DC沿DE方向向左平移，当D平移至点E的位置时，点C恰好与线段BC上的点F重合（如图），请连接AF，并判断△AEF是怎样的三角形，试证明你的结论．

【考点】全等三角形的判定与性质；等边三角形的性质；平移的性质．
【分析】（1）根据已知等边三角形的性质可推出△ADG是等边三角形，从而再利用SAS判定△AGE≌△DAC；
（2）连接AF，由已知可得四边形EFCD是平行四边形，从而得到EF=CD，∠DEF=∠DCF，由（1）知△AGE≌△DAC得到AE=CD，∠AED=∠ACD，从而可得到EF=AE，∠AEF=60°，所以△AEF为等边三角形．
【解答】（1）证明：∵△ABC是等边三角形，
∴AB=AC=BC，∠BAC=∠ABC=∠ACB=60°．
∵EG∥BC，
∴∠ADG=∠ABC=60°∠AGD=∠ACB=60°．
∴△ADG是等边三角形．
∴AD=DG=AG．
∵DE=DB，
∴EG=AB．
∴GE=AC．
∵EG=AB=CA，
∴∠AGE=∠DAC=60°，
在△AGE和△DAC中，
，
∴△AGE≌△DAC（SAS）．
（2）解：△AEF为等边三角形．
证明：如图，连接AF，
∵DG∥BC，EF∥DC，
∴四边形EFCD是平行四边形，
∴EF=CD，∠DEF=∠DCF，
由（1）知△AGE≌△DAC，
∴AE=CD，∠AED=∠ACD．
∵EF=CD=AE，∠AED+∠DEF=∠ACD+∠DCB=60°，
∴△AEF为等边三角形．