

人教版九年级下册28.1 锐角三角函数同步练习题
展开
这是一份人教版九年级下册28.1 锐角三角函数同步练习题,共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
一、选择题(每小题3分,共30分)
1.sin30°=( )
A. B. C. D.
2.的值是( )
A. B.0 C.1 D.
3.在正方形网格中,∠α的位置如图所示,则tanα的值是( )
A. B. C. D.2
4.如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为( ).
A.20海里 B.10海里 C.20海里 D.30海里
5.如图,在综合实践活动中,小明在学校门口的点C处测得树的顶端A仰角为37°,同时测得BC=20米,则树的高AB(单位:米)为( )
A. B.20tan37° C. D.20sin37°
6.如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
A. B. C. D.3
7.在Rt△ABC中,∠C=90°,sinA=,则tanB的值为( )
A. B. C. D.
8.一辆汽车沿倾斜角α的斜坡前进800米,则它上升的高度是( )
A.800•sinα米 B.米 C.800•csα米 D.米
9.在平面直角坐标系中,以原点O为圆心的⊙O交x轴正半轴为M,P为圆上一点,坐标为(,1),则cs∠POM=( )
A. B. C. D.
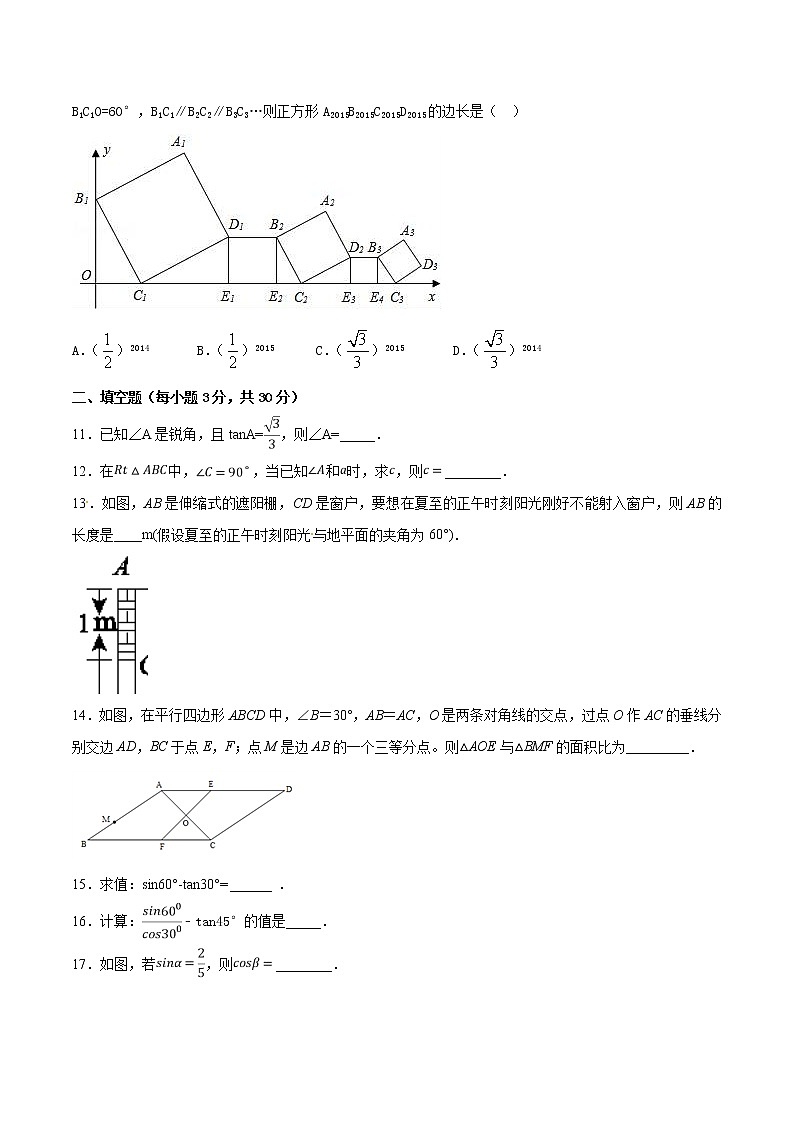
10.在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2015B2015C2015D2015的边长是( )
A.()2014 B.()2015 C.()2015 D.()2014
二、填空题(每小题3分,共30分)
11.已知∠A是锐角,且tanA=,则∠A=_____.
12.在中,,当已知和时,求,则________.
13.如图,AB是伸缩式的遮阳棚,CD是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,则AB的长度是____m(假设夏至的正午时刻阳光与地平面的夹角为60°).
14.如图,在平行四边形ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点。则△AOE与△BMF的面积比为_________.
15.求值:sin60°-tan30°= ______ .
16.计算:﹣tan45°的值是_____.
17.如图,若,则________.
18.如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横截面⊙O的圆心,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=76厘米,∠CED=60°.则垂直支架CD的长度为________厘米(结果保留根号).
19.为加强防汛工作,某市对一拦水坝进行加固,如图,加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB=12米,背水坡面CD=米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE=,则CE的长为______米.
20.如图,在四边形ABCD中,连接AC,BD,AC和BD相交于点E.若AD∥BC,BD⊥AD,2DE=BE, AD=BD,则∠BAC+∠BCA的度数为_______.
三、解答题(共60分)
21.(本题5分).
22.(本题6分)在中俄“海上联合﹣2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cs68°≈0.4,tan68°≈2.5, 1.7)
[来源:Z。xx。k.Cm]
23.(本题6分)一人自地平面上测得塔顶的仰角为60°,于原地登高50米后,又测得塔顶的仰角为30°,求塔高和此人在地面时到塔底的距离.
24.(本题6分)如图,某市对位于笔直公路AC上两个小区A、B的供水路线进行优化改造.供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A、B之间的距离为300(+l)米,求供水站M分别到小区A、B的距离.(结果可保留根号)
25.(本题8分)如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
26.(本题9分)小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20米.
(1)求出大厦的高度BD;
(2)求出小敏家的高度AE.
27.(本题9分)已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.
(1)求OB的长;
(2)求sinA的值.
28.(本题10分)已知:等边△ABC的边长为a.
探究(1):如图1,过等边△ABC的顶点A、B、C依次作AB、BC、CA的垂线围成△MNG,求证:△MNG是等边三角形且MN=a;
探究(2):在等边△ABC内取一点O,过点O分别作OD⊥AB、OE⊥BC、OF⊥CA,垂足分别为点D、E、F.
①如图2,若点O是△ABC的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):结论1.OD+OE+OF=a;结论2.AD+BE+CF=a;
②如图3,若点O是等边△ABC内任意一点,则上述结论1,2是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
(测试时间:120分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.sin30°=( )
A. B. C. D.
【答案】B
【解析】
根据特殊角的三角函数值进行解答即可
2.的值是( )
A. B.0 C.1 D.
【答案】C
【解析】
任何非零实数的零次幂都为1.故选C.
3.在正方形网格中,∠α的位置如图所示,则tanα的值是( )
A. B. C. D.2
【答案】D
【解析】
由图可得,tanα=2÷1=2.
故选D.
4.如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为( ).
A.20海里 B.10海里 C.20海里 D.30海里
【答案】C.
5.如图,在综合实践活动中,小明在学校门口的点C处测得树的顶端A仰角为37°,同时测得BC=20米,则树的高AB(单位:米)为( )
A. B.20tan37° C. D.20sin37°
【答案】B.
【解析】
如图,在直角△ABC中,∠B=90°,∠C=37°,BC=20m,可得tanC=,则AB=BC•tanC=20tan37°.故选B.
6.如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
A. B. C. D.3
【答案】A
7.在Rt△ABC中,∠C=90°,sinA=,则tanB的值为( )
A. B. C. D.
【答案】D
【解析】
∵sinA=,∴设BC=5x,AB=13x,则AC==12x,
故tan∠B==.故选D.
8.一辆汽车沿倾斜角α的斜坡前进800米,则它上升的高度是( )
A.800•sinα米 B.米 C.800•csα米 D.米
【答案】A
9.在平面直角坐标系中,以原点O为圆心的⊙O交x轴正半轴为M,P为圆上一点,坐标为(,1),则cs∠POM=( )
A. B. C. D.
【答案】A
【解析】
作PA⊥x轴于A,
∵点P的坐标为(,1),
∴OA=,PA=1,
由勾股定理得,OP=2,
cs∠POM==,
故选A.
10.在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2015B2015C2015D2015的边长是( )
A.()2014 B.()2015 C.()2015 D.()2014
【答案】D.
二、填空题(每小题3分,共30分)
11.已知∠A是锐角,且tanA=,则∠A=_____.
【答案】30°
【解析】
∵∠A是锐角,tanA=,∴∠A=30°.故答案为:30°.
12.在中,,当已知和时,求,则________.
【答案】
【解析】
如图,
∵已知∠A和a,求c,
∴sinA=,
∴c=.
故选:A.
13.如图,AB是伸缩式的遮阳棚,CD是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,则AB的长度是____m(假设夏至的正午时刻阳光与地平面的夹角为60°).
【答案】
∴,解得:AB=.
故答案为:.
14.如图,在平行四边形ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点。则△AOE与△BMF的面积比为_________.
【答案】
【解析】连接MF,作AG⊥BC交BC于点G,作MH⊥BC交BC于点H,
∴∠EAO=∠ACB=30°,∴OE=OA·tan30°=x,AE==2x,
∴S△AOE=OA·OE=x2,
∵在△AOE和△COF中,
,
∴△AOE≌△COF,
∴AE=CF=2x,
∴BF=6x-2x=4x,
∴S△BMF=BF·MH=2x2,
∴S△AOE∶S△BMF=(x2)∶(2x2)=3∶4.
故答案为3∶4.
15.求值:sin60°-tan30°= ______ .
【答案】
【解析】
原式=-=.
16.计算:﹣tan45°的值是_____.
【答案】0
17.如图,若,则________.
【答案】
【解析】
∵+=90°,
∴.
故答案为:.
18.如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横截面⊙O的圆心,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=76厘米,∠CED=60°.则垂直支架CD的长度为________厘米(结果保留根号).
【答案】38
19.为加强防汛工作,某市对一拦水坝进行加固,如图,加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB=12米,背水坡面CD=米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE=,则CE的长为______米.
【答案】8.
【解析】
分别过A、D作AF⊥BC于点F,DG⊥BC于点G.
在Rt△ABF中,AB=12米,∠B=60°,∴sin∠B=,∴AF=12×=6.
易知四边形AFGD是矩形,∴DG=AF=6.
在Rt△DGC中,CD=12,DG=6,∴GC==18.
在Rt△DEG中,tanE== ,∴EG=26,
∴CE=GE-CG=26-18=8.
故答案为8.
20.如图,在四边形ABCD中,连接AC,BD,AC和BD相交于点E.若AD∥BC,BD⊥AD,2DE=BE, AD=BD,则∠BAC+∠BCA的度数为_______.
【答案】60°
三、解答题(共60分)
21.(本题5分).
【答案】.
【解析】
==.
22.(本题6分)在中俄“海上联合﹣2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cs68°≈0.4,tan68°≈2.5, 1.7)
【答案】308米
解得:x=≈≈308米,
∴潜艇C离开海平面的下潜深度为308米.
23.(本题6分)一人自地平面上测得塔顶的仰角为60°,于原地登高50米后,又测得塔顶的仰角为30°,求塔高和此人在地面时到塔底的距离.
【答案】塔高是75米,此人在地面时到塔底的距离是25米.
【解析】
设BC=x米,则DE=BC=x米.
∵直角△ADE中,tan∠ADE=,
∴AE=DEtan30°=xtan30°=x(米).
同理,直角△ABC中,AC=BCtan60°=x(米),
根据题意得:x﹣x=50,
解得:x=25,
则AC=x=75(米).
答:塔高是75米,此人在地面时到塔底的距离是25米.
24.(本题6分)如图,某市对位于笔直公路AC上两个小区A、B的供水路线进行优化改造.供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A、B之间的距离为300(+l)米,求供水站M分别到小区A、B的距离.(结果可保留根号)
【答案】供水站M到小区A的距离是600米,到小区B的距离是300米.
25.(本题8分)如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
【答案】(1)2米;(2)(6+ EQ \R(,3))或(6- EQ \R(,3))米.
26.(本题9分)小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20米.
(1)求出大厦的高度BD;
(2)求出小敏家的高度AE.
【答案】(1)(20+20)(2)20
在Rt△ACD中,tan30°=,
∴CD=AC•tan30°=20×=20(米),
∴BD=BC+CD=20+20(米);
∴大厦的高度BD为:(20+20)米;
(2)∵四边形AEDC是矩形,
∴AE=CD=20米.
∴小敏家的高度AE为20米.
27.(本题9分)已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.
(1)求OB的长;
(2)求sinA的值.
【答案】(1)(2)
28.(本题10分)已知:等边△ABC的边长为a.
探究(1):如图1,过等边△ABC的顶点A、B、C依次作AB、BC、CA的垂线围成△MNG,求证:△MNG是等边三角形且MN=a;
探究(2):在等边△ABC内取一点O,过点O分别作OD⊥AB、OE⊥BC、OF⊥CA,垂足分别为点D、E、F.
①如图2,若点O是△ABC的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):结论1.OD+OE+OF=a;结论2.AD+BE+CF=a;
②如图3,若点O是等边△ABC内任意一点,则上述结论1,2是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
【答案】(1)证明见解析;(2)①:结论1成立.证明见解析;②:结论2成立.
∴△MNG为等边三角形.
在Rt△ABM中,BM=,
在Rt△BCN中,BN=,
∴MN=BM+BN=a.
(2)①:结论1成立.
证明:如图3,过点O作GH∥BC,分别交AB、AC于点G、H,过点H作HM⊥BC于点M,
∴∠DGO=∠B=60°,∠OHF=∠C=60°,
∴△AGH是等边三角形,
∴GH=AH.
∵OE⊥BC,
∴OE∥HM,
∴四边形OEMH是矩形,
∴HM=OE.
∴OD+OE+OF=OD+HM+OF=OG+HC+OH=(GH+HC)=AC=a.
(2)②:结论2成立.
证明:如图4,连接OA、OB、OC,
根据勾股定理得:
BE2+OE2=OB2=BD2+OD2①,
CF2+OF2=OC2=CE2+OE2②,
AD2+OD2=AO2=AF2+OF2③,
①+②+③得:BE2+CF2+AD2=BD2+CE2+AF2,
∴BE2+CF2+AD2=(a-AD)2+(a-BE)2+(a-CF)2=a2-2AD•a+AD2+a2-2BE•a+BE2+a2-2CF•a+CF2
整理得:2a(AD+BE+CF)=3a2∴AD+BE+CF=a.
相关试卷
这是一份数学九年级下册28.1 锐角三角函数精品复习练习题,共5页。试卷主要包含了计算的结果,正确的是,如图,是的高,若,,则边的长为,的值等于等内容,欢迎下载使用。
这是一份初中数学人教版九年级下册28.1 锐角三角函数课堂检测,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份初中数学人教版九年级下册第二十六章 反比例函数26.1 反比例函数26.1.1 反比例函数达标测试,共23页。










