初中数学人教版九年级下册第二十六章 反比例函数26.1 反比例函数26.1.1 反比例函数达标测试

这是一份初中数学人教版九年级下册第二十六章 反比例函数26.1 反比例函数26.1.1 反比例函数达标测试，共23页。
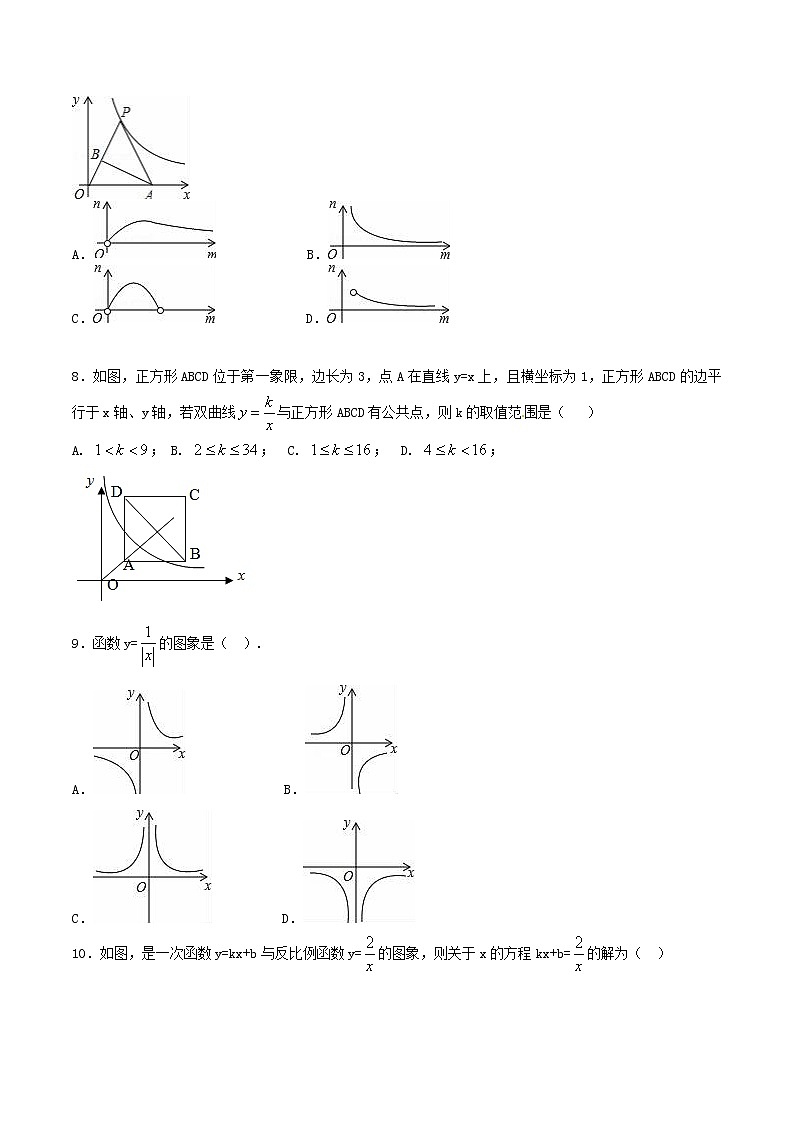
《第二十六章  反比例函数》测试卷（B卷）（测试时间：120分钟     满分：120分）[来源:学+科+网Z+X+X+K]一、选择题（每小题3分，共30分）1．反比例函数y=的图象如图所示，点M是该函数图象上一点，MN垂直于x轴，垂足是点N，如果S△MON=2，则k的值为（  ）．A．2      B．﹣2      C．4      D．﹣42．反比例函数的图象位于（  ）A．第一、二象限   B.第三、四象限     C．第一、象限   D．第二、四象限3．已知点（1，﹣2）在反比例函数的图象上，那么这个函数图象一定经过点（  ）A．（﹣1，2） B．（﹣2，﹣1） C．（﹣1，﹣2） D．（2，1）4．若点P（2，m）是反比例函数图象上一点，则m的值是（  ）A．1              B．2           C．3                 D．45．下列函数中，当x＞0时，y随x的增大而减小的是（    ）A．y=         B．y=-           C．y=3x+2             D．y=x2-36．已知，，是反比例函数的图象上的三点，且，则的大小关系是（  ）A.          B．  C.           D. 7．如图，在平面直角坐标系xOy中，P是反比例函数y=（x＞0）图象上的一个动点，点A在x轴上，且PO=PA，AB是△PAO中OP边上的高．设OA=m，AB=n，则下列图象中，能表示n与m的函数关系的图象大致是（  ）.A．             B．C．             D． 8．如图，正方形ABCD位于第一象限，边长为3，点A在直线y=x上，且横坐标为1，正方形ABCD的边平行于x轴、y轴，若双曲线与正方形ABCD有公共点，则k的取值范围是（   ）[来源:Z.xx.k.Com]A. ； B. ；  C. ；  D. ；9．函数y=的图象是（  ）.A．              B． C．          D．10．如图，是一次函数y=kx+b与反比例函数y=的图象，则关于x的方程kx+b=的解为（  ）[来源:学§科§网]A．xl=1，x2=2                 B．xl=﹣2，x2=﹣1 C．xl=1，x2=﹣2               D．xl=2，x2=﹣1 二、填空题（每小题3分，共30分）11．长方形的面积为，如果它的长是，宽是，那么是的________函数关系，写成的关系式是________．12．已知反比例函数为常数，的图象经过点，则函数的解析式为________．13．在某一电路中，保持电压不变，电流（安）与电阻（欧）成反比例，其图象如图所示，则这一电路中的电压为________伏．14．已知双曲线经过直线y=3x－2与y=x+1的交点，则它的解析式为_________.15．函数y=－x，y=，y＝－x2，y=，y=－中________表示y是x的反比例函数.16．已知某工厂有煤1500吨，则这些煤能用的天数y与每天用煤的吨数x之间的函数关系式为________ ．17．若反比例函数的图象与一次函数y=ax+b的图象交于点A（﹣2，m）、B（5，n），则3a+b的值等于_____．18．反比例函数y=，在x=1处自变量减少，函数值相应增加1，则k=_________.19．如图，菱形AOCB的顶点A坐标为（3，4），双曲线y=（x＞0）的图象经过点B，则k的值为_____．20．已知是同一个反比例函数图像上的两点，若，且，则这个反比例函数的表达式为______________.三、解答题（共60分）21．（本题7分）一次函数的图像与反比例函数的图像交于M(2，m)、N(-1-4) 两点.（1）求反比例函数和一次函数的解析式；（2）根据图像写出使反比例函数值大于一次函数值的x取值范围.      22．（本题7分）如图，Rt△ABO的顶点A是双曲线y=与直线y=在第二象限的交点．AB⊥x轴于B，且S△ABO=．（1）求这两个函数的解析式；（2）求直线与双曲线的两个交点A、C的坐标和 △AOC的面积． 23．（本题7分）平行四边形ABCD的两个顶点A、C在反比例函数（k≠0）图象上，点B、D在x轴上，且B、D两点关于原点对称，AD交y轴于P点（1）已知点A的坐标是（2，3），求k的值及C点的坐标；（2）若△APO的面积为2，求点D到直线AC的距离．   24．（本题7分）如图，反比例函数（x＞0）的图象与直线y=x交于点M，∠AMB=90°，其两边分别与两坐标轴的正半轴交于点A，B，四边形OAMB的面积为6．（1）求k的值；（2）点P在反比例函数（x＞0）的图象上，若点P的横坐标为3，∠EPF=90°，其两边分别与x轴的正半轴，直线y=x交于点E，F，问是否存在点E，使得PE=PF？若存在，求出点E的坐标；若不存在，请说明理由．   25．（本题8分）如图，已知矩形OABC的两边OA、OC分别落在x轴、y轴的正半轴上，顶点B的坐标是（6，4），反比例函数（x＞0）的图象经过矩形对角线的交点E，且与BC边交于点D．（1）①求反比例函数的解析式与点D的坐标；②直接写出△ODE的面积；（2）若P是OA上的动点，求使得“PD+PE之和最小”时的直线PE的解析式．[来源:Zxxk.Com]    26．（本题7分）如图，点A（1，4），B（﹣4，a）在双曲线图象上，直线AB分别交x轴，y轴于C、D，过点A作AE⊥x轴，垂足为E，过点B作BF⊥y轴，垂足为F，连接AF、BE交于点G．（1）求k的值及直线AB的解析式；（2）判断四边形ADFE的形状，并写出证明过程．      27．（本题7分）某地计划用120～180天(含120与180天)的时间建设一项水利工程，工程需要运送的土石方总量为360万立方米．(1)写出运输公司完成任务所需的时间y(单位：天)与平均每天的工作量x(单位：万立方米)之间的函数关系式，并给出自变量x的取值范围；[来源:学。科。网](2)由于工程进度的需要，实际平均每天运送土石方比原计划多5000立方米，工期比原计划减少了24天，原计划和实际平均每天运送土石方各是多少万立方米？    28．（本题10分）如图，正方形AOCB在平面直角坐标系xoy中，点O为原点，点B在反比例函数（x＞0）图象上，△BOC的面积为8．（1）求反比例函数的关系（2）若动点E从A开始沿AB向B以每秒1个单位的速度运动，同时动点F从B开始沿BC向C以每秒2个单位的速度运动，当其中一个动点到达端点时，另一个动点随之停止运动．若运动时间用t表示，△BEF的面积用S表示，求出S关于t的函数关系式？（3）当运动时间为秒时，在坐标轴上是否存在点P，使△PEF的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由．
（测试时间：120分钟     满分：120分）一、选择题（每小题3分，共30分）1．反比例函数y=的图象如图所示，点M是该函数图象上一点，MN垂直于x轴，垂足是点N，如果S△MON=2，则k的值为（  ）．A．2      B．﹣2      C．4      D．﹣4[来源:学#科#网Z#X#X#K]【答案】D【解析】根据k的几何意义可得：，则=4，根据图象在二、四象限可得：k=-4.2．反比例函数的图象位于（  ）A．第一、二象限   B.第三、四象限     C．第一、象限   D．第二、四象限【答案】D3．已知点（1，﹣2）在反比例函数的图象上，那么这个函数图象一定经过点（  ）A．（﹣1，2） B．（﹣2，﹣1） C．（﹣1，﹣2） D．（2，1）【答案】A【解析】先根据点（1，﹣2）在反比例函数的图象上求出k=-2，再根据k=xy的特点对各选项进行逐一判断:A、∵（﹣1）×2=﹣2，∴此点在反比例函数图象上；B、∵（﹣2）×（﹣1）=2≠﹣2，∴此点不在反比例函数图象上；C、∵（﹣1）×（﹣2）=2≠﹣2，∴此点不在反比例函数图象上；D、∵2×1=2≠﹣2，∴此点不在反比例函数图象上．故选A．4．若点P（2，m）是反比例函数图象上一点，则m的值是（  ）A．1              B．2           C．3                 D．4【答案】B【解析】将点P代入反比例函数解析式求出m的值.根据题意得：m==2.5．下列函数中，当x＞0时，y随x的增大而减小的是（    ）A．y=         B．y=-           C．y=3x+2             D．y=x2-3【答案】A6．已知，，是反比例函数的图象上的三点，且，则的大小关系是（  ）A.          B．  C.           D. 【答案】C【解析】对于反比例函数，当x＞0时，y＞0；当x＜0时，y＜0，则本题中最大；在每一个象限内，y随x的增大而减小，因为，所以；∴＞.7．如图，在平面直角坐标系xOy中，P是反比例函数y=（x＞0）图象上的一个动点，点A在x轴上，且PO=PA，AB是△PAO中OP边上的高．设OA=m，AB=n，则下列图象中，能表示n与m的函数关系的图象大致是（  ）.A．             B．C．             D．【答案】A.8．如图，正方形ABCD位于第一象限，边长为3，点A在直线y=x上，且横坐标为1，正方形ABCD的边平行于x轴、y轴，若双曲线与正方形ABCD有公共点，则k的取值范围是（   ）A. ； B. ；  C. ；  D. ；【答案】C【解析】根据题意可得：点A的坐标为(1，1)，根据正方形的边长可得：点C的坐标为(4，4)，根据题意可得k的取值范围为：.9．函数y=的图象是（  ）.[来源:学*科*网]A．              B． C．          D．【答案】C.10．如图，是一次函数y=kx+b与反比例函数y=的图象，则关于x的方程kx+b=的解为（  ）A．xl=1，x2=2                B．xl=﹣2，x2=﹣1 C．xl=1，x2=﹣2               D．xl=2，x2=﹣1【答案】C．【解析】由图可知，两函数图象的交点坐标为（1，2），（﹣2，﹣1），即可得关于x的方程kx+b=的解为xl=1，x2=﹣2．故选C．二、填空题（每小题3分，共30分）11．长方形的面积为，如果它的长是，宽是，那么是的________函数关系，写成的关系式是________．【答案】反比例,        [来源:学科网]12．已知反比例函数为常数，的图象经过点，则函数的解析式为________．【答案】．【解析】∵反比例函数y=（k为常数，k≠0）的图象经过点P（3，3），∴3=，∴k=9，∴反比例函数的解析式为：y=．故答案为：y=．13．在某一电路中，保持电压不变，电流（安）与电阻（欧）成反比例，其图象如图所示，则这一电路中的电压为________伏．【答案】【解析】由题意可知：保持电压不变，电流I（安）与电阻R（欧）成反比例，设R=，即U=IR，由图象上的一点坐标为（2，6），即I=2（安），R=6（欧），∴U=2×6=12（伏）．[来源:Z_xx_k.Com]故答案为：12．14．已知双曲线经过直线y=3x－2与y=x+1的交点，则它的解析式为_________.【答案】y=则函数解析式为y=.故答案为y=.15．函数y=－x，y=，y＝－x2，y=，y=－中________表示y是x的反比例函数.【答案】y=， y=－ 【解析】函数y=－x，y=，y＝－x2，y=，y=－中，只有y=， y=－表示y是x的反比例函数.故答案为：y=， y=－16．已知某工厂有煤1500吨，则这些煤能用的天数y与每天用煤的吨数x之间的函数关系式为________ ．【答案】y= 【解析】∵煤的总吨数为1500，平均每天用煤的吨数为x，∴这些煤能用的天数为y=，故答案为：y=．17．若反比例函数的图象与一次函数y=ax+b的图象交于点A（﹣2，m）、B（5，n），则3a+b的值等于_____．[来源:Z*xx*k.Com]【答案】021a+7b=0，即3a+b=0.故答案为：0.18．反比例函数y=，在x=1处自变量减少，函数值相应增加1，则k=_________.【答案】1【解析】在y=中，当x=1时，y=k，因为在x=1处，自变量减少，函数值相应增加1，即x=0.5时，函数值是y+1，得，即解得.故答案为：119．如图，菱形AOCB的顶点A坐标为（3，4），双曲线y=（x＞0）的图象经过点B，则k的值为_____．【答案】32∴OM=3，AM=4，由勾股定理得：OA=5，即OC=OA=AB=BC=5，在△AOM和△BCN中，∴△AOM≌△BCN（AAS），∴BN=AM=4，CN=OM=3，∴ON=5+3=8，即B点的坐标是（8，4），把B的坐标代入y=，得：k=32，故答案为：32.20．已知是同一个反比例函数图像上的两点，若，且，则这个反比例函数的表达式为______________.【答案】 三、解答题（共60分）21．（本题7分）一次函数的图像与反比例函数的图像交于M(2，m)、N(-1-4) 两点.（1）求反比例函数和一次函数的解析式；（2）根据图像写出使反比例函数值大于一次函数值的x取值范围.【答案】(1)、y=；y=2x－2；(2)、x<－1或0<x<2.【解析】 (1)、将点N代入反比例函数可得：k=4 ， 则反比例函数的解析式为：y=将点M代入解析式可得：m=2    则点M的坐标为(2，2)将M、N代入一次函数解析式可得：   解得：    ∴一次函数的解析式为：y=2x－2(2)、根据函数的交点以及图像可得：当x<－1或0<x<2时，反比例函数值大于一次函数值.22．（本题7分）如图，Rt△ABO的顶点A是双曲线y=与直线y=在第二象限的交点．AB⊥x轴于B，且S△ABO=．（1）求这两个函数的解析式；（2）求直线与双曲线的两个交点A、C的坐标和 △AOC的面积．【答案】（1）y=-，y=﹣x+2（2）A为（﹣1，3），C为（3，﹣1）,4（2）由y=﹣x+2，令x=0，得y=2．∴直线y=﹣x+2与y轴的交点D的坐标为（0，2），A、C两点坐标满足解得或∴交点A为（﹣1，3），C为（3，﹣1），∴S△AOC=S△ODA+S△ODC=OD·（|x1|+|x2|）=×2×（3+1）=4．23．（本题7分）平行四边形ABCD的两个顶点A、C在反比例函数（k≠0）图象上，点B、D在x轴上，且B、D两点关于原点对称，AD交y轴于P点（1）已知点A的坐标是（2，3），求k的值及C点的坐标；（2）若△APO的面积为2，求点D到直线AC的距离．【答案】（1）k=6，C（﹣2，﹣3）；（2）．（2）∵△APO的面积为2，点A的坐标是（2，3），∴2=，得OP=2，设过点P（0，2），点A（2，3）的直线解析式为y=ax+b，则，解得：，即直线PC的解析式为，将y=0代入，得x═﹣4，∴OP=4，∵A（2，3），C（﹣2，﹣3），∴AC==，设点D到AC的距离为m，∵S△ACD=S△ODA+S△ODC，∴，解得，m=，即点D到直线AC的距离是．24．（本题7分）如图，反比例函数（x＞0）的图象与直线y=x交于点M，∠AMB=90°，其两边分别与两坐标轴的正半轴交于点A，B，四边形OAMB的面积为6．（1）求k的值；（2）点P在反比例函数（x＞0）的图象上，若点P的横坐标为3，∠EPF=90°，其两边分别与x轴的正半轴，直线y=x交于点E，F，问是否存在点E，使得PE=PF？若存在，求出点E的坐标；若不存在，请说明理由．【答案】（1）6；（2）E（4，0）或E（6，0）．①如图2，过点P作PG⊥x轴于点G，过点F作FH⊥PG于点H，交y轴于点K．∵∠PGE=∠FHP=90°，∠EPG=∠PFH，PE=PF，∴△PGE≌△FHP，∴PG=FH=2，FK=OK=3﹣2=1，GE=HP=2﹣1=1，∴OE=OG+GE=3+1=4，∴E（4，0）；②如图3，过点P作PG⊥x轴于点G，过点F作FH⊥PG于点H，交y轴于点K．∵∠PGE=∠FHP=90°，∠EPG=∠PFH，PE=PF，∴△PGE≌△FHP，∴PG=FH=2，FK=OK=3+2=5，GE=HP=5﹣2=3，∴OE=OG+GE=3+3=6，∴E（6，0）．综上所述，E（4，0）或E（6，0）．25．（本题8分）如图，已知矩形OABC的两边OA、OC分别落在x轴、y轴的正半轴上，顶点B的坐标是（6，4），反比例函数（x＞0）的图象经过矩形对角线的交点E，且与BC边交于点D．（1）①求反比例函数的解析式与点D的坐标；②直接写出△ODE的面积；（2）若P是OA上的动点，求使得“PD+PE之和最小”时的直线PE的解析式．【答案】（1）①D（1.5，4），②4.5；（2）y=﹣4x+10．26．（本题7分）如图，点A（1，4），B（﹣4，a）在双曲线图象上，直线AB分别交x轴，y轴于C、D，过点A作AE⊥x轴，垂足为E，过点B作BF⊥y轴，垂足为F，连接AF、BE交于点G．（1）求k的值及直线AB的解析式；（2）判断四边形ADFE的形状，并写出证明过程．【答案】（1）k=4，y=x+3；（2）平行四边形，证明见解析.（2）四边形ADFE为平行四边形,在y=x+3中，当x=0时，y=3，∴D（0，3），即OD=3，∵B（﹣4，﹣1），BF⊥y轴，∴OF=1，∴DF=3+1=4，又∵A（1，4），AE⊥x轴，∴AE=4，∴AE=DF，又∵AE∥DF，∴四边形ADFE为平行四边形．27．（本题7分）某地计划用120～180天(含120与180天)的时间建设一项水利工程，工程需要运送的土石方总量为360万立方米．(1)写出运输公司完成任务所需的时间y(单位：天)与平均每天的工作量x(单位：万立方米)之间的函数关系式，并给出自变量x的取值范围；(2)由于工程进度的需要，实际平均每天运送土石方比原计划多5000立方米，工期比原计划减少了24天，原计划和实际平均每天运送土石方各是多少万立方米？【答案】(1)y=(2≤x≤3)；(2)原计划每天运送2.5万立方米，实际平均每天运送3万立方米【解析】28．（本题10分）如图，正方形AOCB在平面直角坐标系xoy中，点O为原点，点B在反比例函数（x＞0）图象上，△BOC的面积为8．（1）求反比例函数的关系（2）若动点E从A开始沿AB向B以每秒1个单位的速度运动，同时动点F从B开始沿BC向C以每秒2个单位的速度运动，当其中一个动点到达端点时，另一个动点随之停止运动．若运动时间用t表示，△BEF的面积用S表示，求出S关于t的函数关系式？（3）当运动时间为秒时，在坐标轴上是否存在点P，使△PEF的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由． 【答案】(1)y=；(2)S=－+4；(3)P(，0)【解析】 (1)∵四边形AOCB为正方形，   ∴AB=BC=OC=OA，设点B坐标为（a，a），∵C=8，∴=8，   ∴a=±4    又∵点B在第一象限，∴点B坐标为（4，4），将点B（4，4）代入y=得，k=16    ∴反比例函数解析式为y=(2)∵运动时间为t，∴AE=t，BF=2t   ∵AB=4，∴BE=4-t，∴=(4-t)•2t=-+4t=-－+4，