初中数学人教版八年级上册15.3 分式方程教学演示课件ppt

这是一份初中数学人教版八年级上册15.3 分式方程教学演示课件ppt，共43页。PPT课件主要包含了常见的相等关系，工程问题，等量关系时间相等，15x，试一试，议一议，有什么区别和联系，x-1，x1+50%等内容，欢迎下载使用。

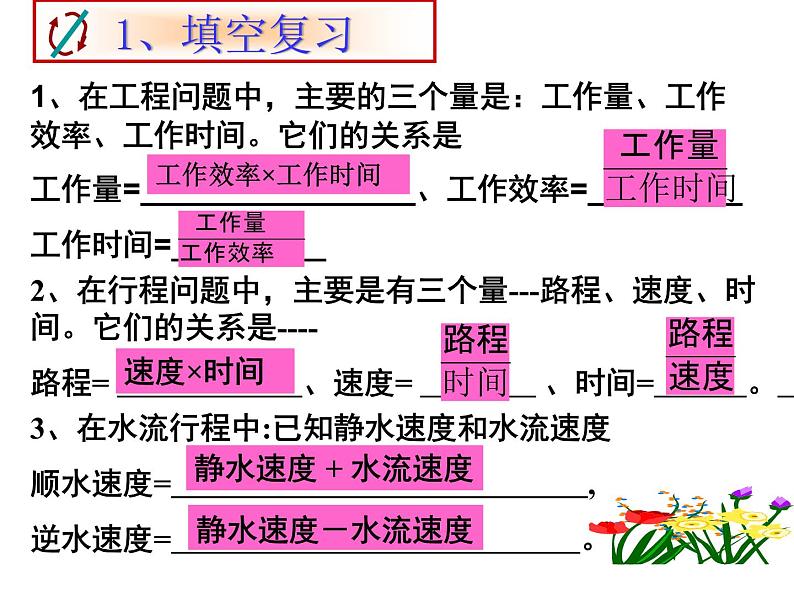
2、在行程问题中，主要是有三个量---路程、速度、时间。它们的关系是----路程= 、速度= 、时间= 。
3、在水流行程中:已知静水速度和水流速度顺水速度= ,逆水速度= 。
静水速度 + 水流速度
1、在工程问题中，主要的三个量是：工作量、工作效率、工作时间。它们的关系是工作量=________________、工作效率=_________工作时间=_________
(1)、相遇问题 ：甲行程 + 乙行程 =全路程
(2)、追及问题： (设甲的速度快)
1)、同时不同地： 甲用的时间 = 乙用的时间 甲的行程 - 乙的行程 = 甲乙原来相距的路程
2)、同地不同时： 甲用的时间 = 乙用的时间 - 时间差 甲走的路程 = 乙走的路程
3)、水(空)航行问题 ： 顺流速度 = 静水中航速 + 水速 逆流航速 = 静水中速度 – 水速
工作量 = 工作效率 X 工作时间
甲的工作量+乙的工作量 = 合作工作量
注：工作问题常把总工程看作是单位1，水池注水问题也属于工程问题
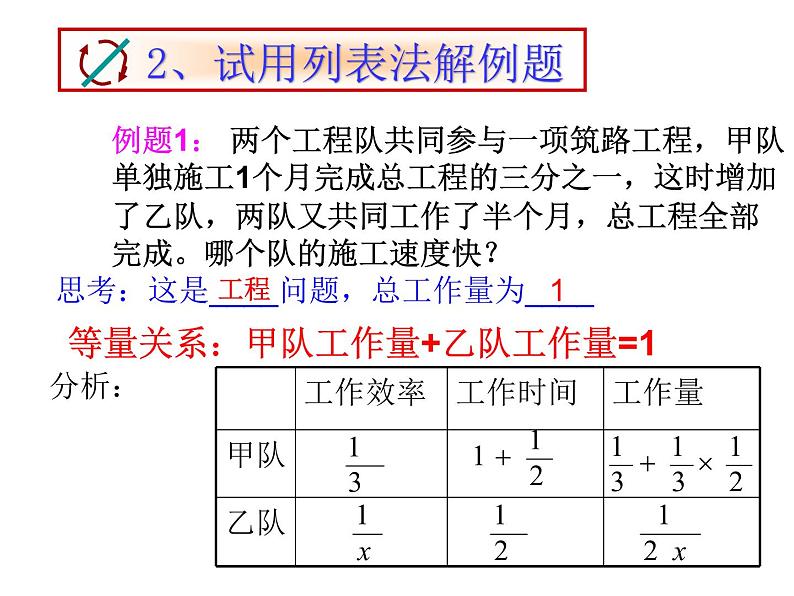
例题1： 两个工程队共同参与一项筑路工程，甲队单独施工1个月完成总工程的三分之一，这时增加了乙队，两队又共同工作了半个月，总工程全部完成。哪个队的施工速度快？
思考：这是____问题，总工作量为____
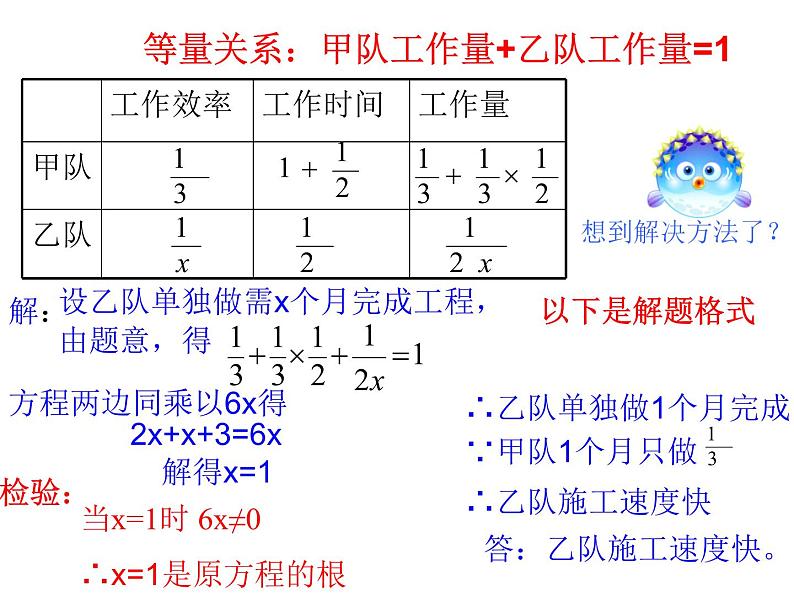
等量关系：甲队工作量+乙队工作量=1
设乙队单独做需x个月完成工程，由题意，得
当x=1时 6x≠0∴x=1是原方程的根
∴乙队单独做1个月完成
例题2：从2004年5月起某列车平均提速v千米/小时，用相同的时间，列车提速前行驶s千米，提速后比提速前多行驶50千米，提速前列车的平均速度为多少？
思考：这是____问题
设提速前列车的平均速度为x千米/时由题意，得
注意： s、v的实际意义
在方程两边同乘以x(x+v)得:
s(x+v)=x(s+50)
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.2.设:选择恰当的未知数,注意单位和语言完整.3.列:根据数量和相等关系,正确列出代数式和方程.4.解:认真仔细.5.验:有两次检验.6.答:注意单位和语言完整.且答案要生活化.
两次检验是:(1)是否是所列方程的解;(2)是否满足实际意义.
练习1、 A、B两种机器人都被用来搬运化工原料，A型 机器人比B型机器人每小时多搬运30kg，A型机器人搬运900kg所用时间与B型机器人搬运600kg所用时间相等，两种机器人每小时分别搬运多少化工原料？
思考：这是____问题，三个工作量为____________________
工作量、工作效率、工作时间
设A种机器人每小时搬运x kg，由题意得
检验：当x=90时，x(x-30)≠0∴ x=90是原方程的根
答：A和B两种机器人每小时分别能搬90kg和60kg。
在方程两边都乘以x(x-30)得
900(x-30)=600x
例2. 甲、乙两人做某种机器零件，已知甲每小时比乙多做6个，甲做90个零件所用的时间和乙做60个零件所用时间相等，求甲、乙每小时各做多少个零件？
解：设甲每小时做x个零件则乙每小时做（ x －6）个零件， 依题意得：
经检验X=18是原方程的根,且符合题意。
答：甲每小时做18个，乙每小时12个
我们所列的是一个分式方程，这是分式方程的应用
由x＝18得x－6=12
等量关系：甲用时间=乙用时间
练习2、某工程队需要在规定日期内完成。若甲队单独做正好按时完成；若乙队单独做，超过规定日期三天才能完成。现由甲、乙合作两天，余下工程由乙队单独做，恰好按期完成，问规定日期是多少天？
等量关系：甲完成的工作量+乙完成的工作量=总工作量
等量关系：甲完成的工作量+乙完成的工作量=总做总量
设规定日期是x天，由题意，得
检验：当x=6时，x(x+3)≠0∴ x=6是原方程的根
在方程两边都乘以x(x+3)得:
2(x+3)+x=x(x+3)
重庆市政府打算把一块荒地建成公园，动用了一台甲型挖土机，4天挖完了这块地的一半。后又加一台乙型挖土机，两台挖土机一起挖，结果1天就挖完了这块地的另一半。乙型挖土机单独挖这块地需要几天？
(1)设乙型挖土机单独挖这块地需要x天,那么它1天挖土量是这块地的_______;
分析:请完成下列填空:
(2)甲型挖土机1天挖土量是这块地的______;
(3)两台挖土机合挖,1天挖土量是这块地的_____.
我部队到某桥头阻击敌人，出发时敌军离桥头24Km，我部队离桥头30Km，我部队急行军速度是敌人的1.5倍，结果比敌人提前48分钟到达，求我部队急行军的速度。
我军的时间= 敌军的时间
解：设敌军的速度为X千米/时,则我军为1.5X千米/时。
由题意得方程：
设敌军的速度为X千米/时
农机厂到距工厂15千米的向阳村检修农机，一部分人骑自行车先走，过了40分钟，其余人乘汽车去，结果他们同时到达，已知汽车的速度是自行车的3倍，求两车的速度。
分析：设自行车的速度是x千米/时，汽车的速度是3x千米/时
请根据题意填写速度、时间、路程之间的关系表
请找出可列方程的等量关系
自行车先走 时
解：设自行车的速度为x千米/时，那么汽车的速度是3x千米/时， 依题意得：
汽车所用的时间＝自行车所用时间－ 时
经检验，15是原方程的根
由x＝15得3x=45
答：自行车的速度是15千米/时，汽车的速度是45千米/时
例1：农机厂到距工厂15千米的向阳村检修农机，一部分人骑自行车先走，过了40分钟，其余人乘汽车去，结果他们同时到达，已知汽车的速度是自行车的3倍，求两车的速度。
练习3、八年级学生去距学校10千米的博物馆参观，一部分同学骑自行车先走，过了20分后，其余同学乘汽车出发，结果他们同时到达。已知汽车的速度是骑车同学速度的2倍，求骑车同学的速度。
思考：这是____问题，三个量为____________________
设骑车同学的速度为x千米/时，由题意，得
答：骑车同学的速度为15千米/时。
检验：当x=15时，2x≠0∴ x=15是原方程的根
在方程两边都乘以2x得:
练习4、甲、乙两人分别从相距目的地6千米和10千米的两地同时出发，甲、乙的速度比是3：4，结果甲比乙提前20分到达目的地。求甲、乙的速度。
设甲的速度x千米/时，则乙的速度是3x千米/时由题意得
答：甲的速度4.5千米/时，乙的速度是6千米/时。
∴ 3x=4.5 ，4x=6
检验：当x=1.5时，12x≠0∴ x=1.5是原方程的根
在方程两边都乘以12x得:
练习5、一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水,向容器中注满水的全过程共用时间t分。求两根水管各自的注水速度。 （提示：要考虑大水管的进水速度是小水管进水速度的多少倍）
等量关系：小水管注水时间+大水管注水时间=t分
大水管口径是小水管的2倍，则大水管的截面积是小水管的4倍，那么大水管的进水速度是小水管的4倍。
大水管的进水速度是小水管的4倍。
设小水管注水的速度x立方米/分，则大水管注水的速度4x立方米/分，由题意得
在方程两边都乘以8x得:
等量关系：第二组用的时间-第一组用的时间=15分钟
练习6、两个小组同时开始攀登一座450米高的山，第一组的速度是第二组的1.2倍，他们比第二组早15分到达顶峰，两个小组的速度各是多少？ （若山高h米，第一组的速度是第二组的a倍，并比第二组早t分到达顶峰，则两组速度各是多少？）
设第二组的速度x米/分，则第一组的速度是1.2x米/分由题意得
答：第一组的速度6米/分，第二组的速度是5米/分。
检验：当x=5时，12x≠0∴ x=5是原方程的根
5400-4500=180x
等量关系：第二组用的时间-第一组用的时间=t分钟
设第二组的速度x米/分，则第一组的速度是ax米/分由题意得
在方程两边都乘以ax得:
工厂生产一种电子配件,每只成本为2元,利率为25%.后来通过工艺改进,降低成本,在售价不变的情况下,利率增加了15%.问这种配件每只的成本降低了多少?
设这种配件每只的成本降低了x元,
售价=成本（1+利率）
抓住原售价=现售价，得
现售价=现成本（1+现利率）
原售价=原成本（1+原利率）
一轮船往返于A、B两地之间，顺水比逆水快1小时到达。已知A、B两地相距80千米，水流速度是2千米/小时，求轮船在静水中的速度。
假设：轮船在静水中的速度是X千米/小时。
根据题意得：顺水比逆水快一个小时到达。
X=－18（不合题意，舍去）
解：设船在静水中的速度为X千米/小时。
80X+160 －80X+160=X2 －4
答：船在静水中的速度为18千米/小时。
甲、乙两种商品，已知甲的价格每件比乙多6元，买甲90件所用的钱和买乙60件所用钱相等，求甲、乙每件商品的价格各多少元？
1、 甲、乙两人练习骑自行车，已知甲每小时比乙多走6千米，甲骑90千米所用的时间和乙起骑60千米所用时间相等，求甲、乙每小时各骑多少千米？
2、甲、乙两种商品，已知甲的价格每件比乙多6元，买甲90件所用的钱和买乙60件所用钱相等，求甲、乙每件商品的价格各多少元？
1. 甲、乙两人做某种机器零件，已知甲每小时比乙多做6个，甲做90个零件所用的时间和乙做60个零件所用时间相等，求甲、乙每小时各做多少个零件？
2. 甲、乙两人练习骑自行车，已知甲每小时比乙多走6千米，甲骑90千米所用的时间和乙起骑60千米所用时间相等，求甲、乙每小时各骑多少千米？
3.甲、乙两种商品，已知甲的价格每件比乙多6元，买甲90件所用的钱和买乙60件所用钱相等，求甲、乙每件商品的价格各多少元？
数量关系和所列方程相同
即：两个量的积等于第三个量
一是工作问题，二是行程问题，三是价格问题
练习2：甲、乙二人同时从张庄出发，步行15千米到李庄。甲比乙每小时多走1千米，结果比乙早到半小时。二人每小时各走多少千米？
解：设甲速度为x千米/时，则乙速度为________千米/时
练习1：某农场开挖一条长960米的渠道，开工后工作效率比计划提高50%，结果提前4天完成任务。原计划每天挖多少米？
解：设原计划每天挖x米，则实际每天挖 _________ __ 米。
例1、甲乙两人 分别骑摩托车从A、B两地相向而行，甲先行1小时之后，乙才出以，又经过4小时，两人在途中的C地相遇，相遇后，两人按原来的方向继续前行，乙在由C地到A地的途中因故停了20分钟，结果乙由C地到A地时，比甲由C地到B地还提前了40分钟，已知乙比甲每小时多行4千米，求甲乙两车的速度。
分析：本题把时间作为考虑的着眼点。 设甲的速度为 x 千米/时 1)、相等关系：乙的时间=甲的时间
解：设甲每小时行驶x千米，那么乙每小时行驶(x+4)千米 根据题意，得
解之得， x1=16, x2= - 2, 都是原方程的根 但x= - 2 不合题意，舍去
所以x=16时， x+4=20
答：甲车的速度为16千米/小时，乙车的速度为20千米/小时。
2、老师小结：列表法可以方便理解解应用题。列表是一种手段而不是目的，平常做应用题可在心中自有一张表格，逐项理清，而不必都要列在纸上。
1、学生小结（心情、知识点、疑惑处等）
首先你要相信自己，然后你才能干好事情！